2. Відношення.

Поняття “відношення” поширене як в математиці так і за її межами.

Так, наприклад, говорять про родинні відносини між певними людьми, про відносини між людьми на роботі. В математиці говорять про відношення подільності чисел, паралельності та перпендикулярності прямих на площині, подібності фігур і т.д.

Основну ідею поняття “відношення” можна розглянути на таких прикладах:

А={3;5;8}, В={1;4;11}

Побудуємо множини правильних висловлень:

М₁={“3:1”, ”5:1”, ”8:1”, ”8:4”}

М₂={“3>1”, ”5>1”, ”8>1”, ”5>4”, ”8>4”}

Кожний елемент з множини М₁ є висловлення про відношення подільності, а кожний елемент з множини М₂ є висловлення про відношення “більше”.

Кожне з висловлень множини М₁ можна замінити відповідною парою (а; b), в якій аА, bВ, тоді матимемо множину таких пар: ={(3;1), (8;1), (5;1), (8;4)}, яка є підмножиною прямого добутку множин А і В: (А×В). Отже, замість множини , яка характеризує відношення подільності в множинах А і В, можна розглядати множину відповідних пар.

Відношення “більше” в множинах А і В можна зобразити відповідною множиною пар (а;b), в яких перша компонента аА більша другої компоненти bМ, тобто є підмножиною прямого добутку множин А і В:

={(3;1), (5;1), (8;1), (5;4), (8;4)}.

Бінарним відношенням, визначеним у множинах А і В називається кожна підмножина прямого добутку множин А і В.

Позначають: α, β, γ,…Ρ, Μ, Ν…

Якщо А=В, то кажуть, що бінарне відношення визначене у множині А.

Відношення полягають у тому, що деяким елементам множини А поставлені у відповідність елементи множини В. Множина А називається множиною відправлення (визначення), а множина В - множиною прибуття (значень).

Під об’ємом відношення α розуміють склад тих пар, які входять в α.

Якщо елементи а і b пари (а;в) перебувають у відношенні α, то позначають так : (а;в)α або а α в.

В утворенні пар бінарного відношення можуть брати участь не всі елементи множин А і В.

Способи задання відношень.

1. переліком всіх своїх елементів;

2. характеристичною властивістю:

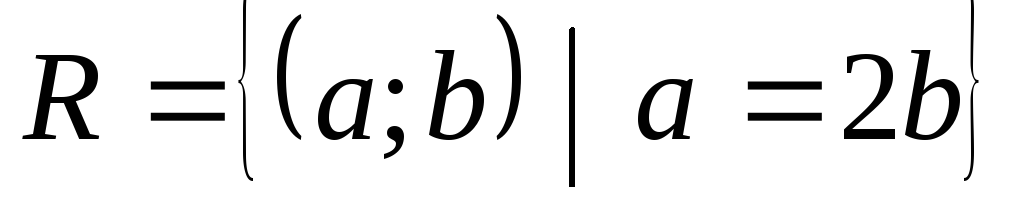
3. графічно (множиною точок на площині): А={1;2;3;4;5}, В={а; b;с;d}

А В	1	2	3	4	5
a
b
c
d

4. с

   1

   a

   трілковий:

2

b

3

c

4

d

5

5)табличний:

B\A	1	2	3	4	5
a	×		×
b			×		×
c			×	×
d					×

Множина всіх bВ, які відповідають елементу а, називаються образом а в В при відповідності Р. Множина всіх а А, яким відповідають елементи bВ називаються

прообразом b в А.

Відношенням оберненим до Р ( РА×В) називається відношення Р^-1, що є підмножиною прямого добутку В×А і складається з тих і тільки тих пар (b;а), для яких (а;b)Р.

Позначають: Р^-1, α ^–1 : (b;а)Р (а; b)Р

Приклад: А={3;4;6;7}, В={2;3;4}. Задати Р^-1, де Р –відношення подільності.

Р={(3;3), (4;4), (4;2), (6;2), (6;3)}, Р^-1= {(3;3), (4;4), (2;4), (2;6), (3;6)}

З означення випливає, що обернене до відношення Р^-1 буде відношення Р: (Р ^-1)^-1 = Р

Щоб дістати стрілкове відношення Р^-1, треба стрілки відношення Р поміняти на протилежні.

Композицією відношень називається послідовне застосування двох відношень.

Композиція відношень - це операція з трьома множинами Χ, Υ, Ζ на яких визначені дві відповідності Р і Q: (Х;Y;Р) і (Y;Z;Q), де РX×Y, QY×Z

Композицію позначають Р ο Q, при цьому композицію відношень записують:

(X, Z, P ο Q), P ο Q X × Z.

Властивості відношень.

1) рефлексивність: аА; а R а (елемент а знаходиться у відношенні R сам до себе).

Якщо властивість рефлексивності не виконується, то відношення називається антирефлексивним: аА; .

2) симетричність:а, вА, а R в в R а

Якщо властивість симетричності не виконується, то відношення називається антисиметричним:

Асиметричне відношення: 

3) транзитивність:а, в, с А, а R b і b R с а R с.

Якщо властивість транзитивності не виконується, то відношення називається антитранзитивним: а, в, с А, а R b і b R с .

4) властивість повноти:а, b А, а ≠ b, то а R b або b R а.

Відношення називається еквівалентним, якщо одноразово виконуються властивості рефлексивності, симетричності і транзитивності. Еквівалентність розбиває множину на підмножини.

Відношення строгого порядку, якщо воно асиметричне і транзитивне одночасно.

Відношення нестрогого порядку, якщо воно асиметричне, транзитивне і рефлексивне.