5. Дерево.

Зв’язний граф без циклів називається деревом.

«Зв’язний » означає, що його не можна розбити на два не розірвавши в якій–небудь вершині. З прикладами дерев ви зустрічаєтесь при роботі в NORTON COMMANDER – дерево каталогів, що будується за допомогою клавіш Ctrl +T.

Теорема: граф є деревом тоді і тільки тоді, коли будь-які дві вершини сполучені рівно одним простим шляхом.

Вершина графа з якої виходить рівно одне ребро, називається «висячою». Оскільки у графа кількість вершин скінчена, то така подорож обов’язково закінчиться, а закінчитись вона може лише у «висячій» вершині.

Лема про «висячу» вершину: кожне дерево, яке має не менше двох вершин, має хоча б дві «висячі» вершини.

Теорема: в дереві кількість вершин на одну більше за кількість ребер.

m=n-1, де m - вершини, n - ребра.

Вершини дерева, які мають степінь один називаються листками (кінцевими вершинами). Останні вершини дерева, які не є кінцевими, називаються внутрішніми. Відстанню між двома вершинами дерева називається число ребер ланцюга, який з’єднує ці вершини. Дерева, в яких виділена (зафіксована) одна вершина називаються кореневими, а ця вершина називається коренем.

Сукупність вершин, які знаходяться на відстані k ребер від кореня називаються

k - ярусом дерева.

Бінарним (орієнтованим) деревом називається дерево, яке задовольняє умовам:

1. в кореневу вершину не входить ні одна дуга;

2. будь-яка інша вершина має тільки одну дугу, яка входить в неї і тільки або дві, або жодної дуги, яка виходить з неї.

Приклади. Множина чотирикутників зображена у вигляді дерева.

Чотирикутники

паралелограми

ромб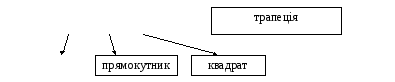

Множина чисел зображена у вигляді дерева.

Комплексні, а+ві

Дерево розбору арифметичного виразу:

6. Транспортні мережі.

Транспортною мережею називається скінчений граф без петель, який задовольняє умови:

• існує лише одна вершина 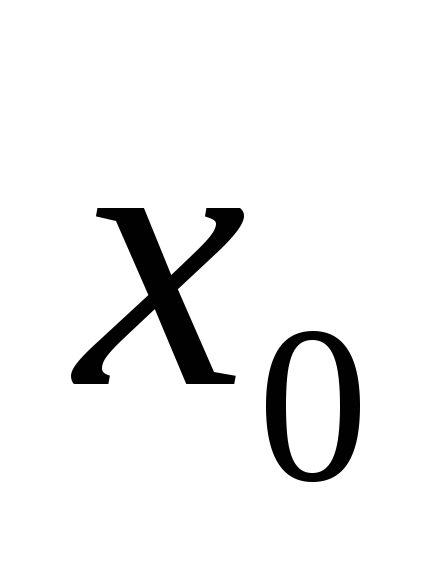, яка називається входом (джерелом) мережі;

• існує лише одна вершина 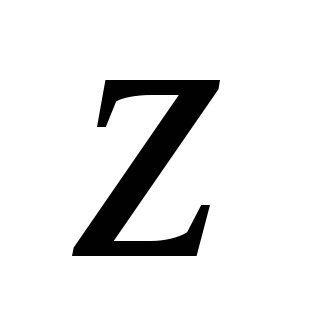, яка називається виходом (витоком) мережі;

• кожному ребру (дузі) 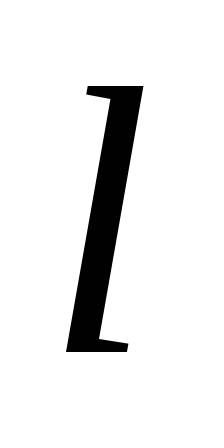приписується число 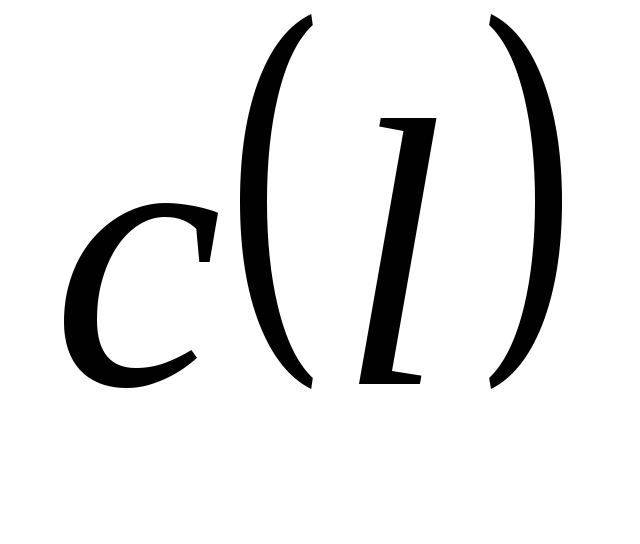, яке називається пропускною здатністю ребра .

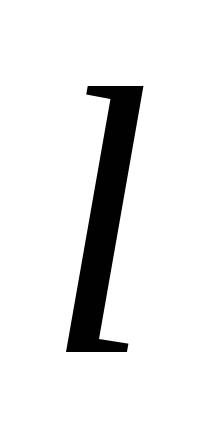З поняттям транспортної мережі пов’язують поняття потоку. Нехай - довільна вершина транспортної мережі. Позначимо через - множину всіх дуг, що заходять в дану вершину, а через - множину всіх дуг, що виходять з даної вершини.

Потоком по дузі транспортної мережі називається функція , яка задовольняє умовам:

1. 

2. 

Функцію можна розглядати як кількість речовини, енергії або об’єктів, які протікають по ребру від вершини до вершини . Згідно умови 1 ця кількість не може перевищувати пропускної здатності ребра. Згідно умови 2 потік, який заходить в вершину дорівнює потоку, який виходить з вершини. Таким чином потік не може накопичуватись в жодній вершині транспортної мережі, крім вхідної та вихідної вершини.

- величина потоку транспортної мережі.

До аналізу транспортної мережі зводяться задачі, які виникають в процесі планування поставок матеріалів, розподілу потоків речовини, енергії, товарів між споживачами.

Нехай А – деяка множина вершин транспортної мережі (), яка задовольняє умовам: .позначимо і - множини ребер, які відповідно входять і виходять в вершини, які належать множині А. Повну сукупність називають розрізом транспортної мережі.

Оскільки кожна частина речовини, що рухається від до , обов’зково буде проходити через дуги розрізу, то загальний потік через розріз дорівнює потоку транспортної мережі

Пропускна здатність розрізу А () – це сума пропускних здатностей дуг, що заходять в вершини розрізу: ,

Задача про найбільший потік: при заданій конфігурації транспортної мережі та відомій пропускній здатності ребер необхідно знайти найбільше значення потоку, який може пропустити транспортна мережа, а також розподіл цього потоку по ребрах мережі.

Дуга називається насиченою, коли величина потоку ребра дорівнює пропускній здатності цього ребра: .

Повний потік – це такий потік , кожний шлях якого від до містить хоча б одну насичену дугу.

Алгоритм для знаходження потоку був запропонований Фордом та Фалкерсоном і полягає в поступовому збільшенні потоку до тих пір, поки він не стане найбільшим.

Знаходження найбільшого потоку складається з двох етапів.

 етап. Знаходження повного потоку: нехай - деякий розподіл потоків по дугам транспортної мережі (його задають). Шукаємо шляхи , які містять всі ненасичені дуги і припускаємо, що

 етап. Знаходження найбільшого потоку. Нехай - повний потік.

1. проводимо розподіл потоку 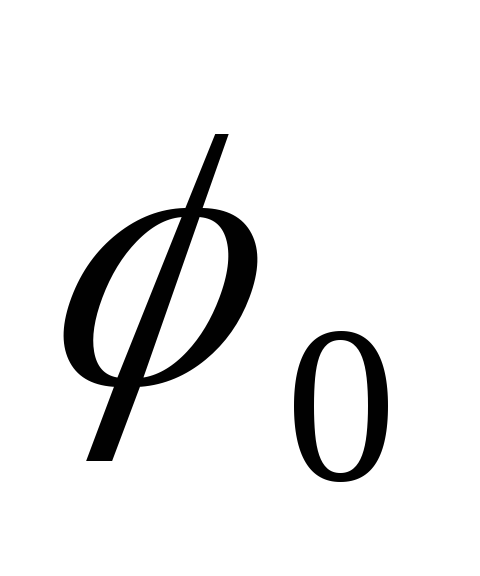по ребрам мережі;

2. приписування індексів вершинам: вершині 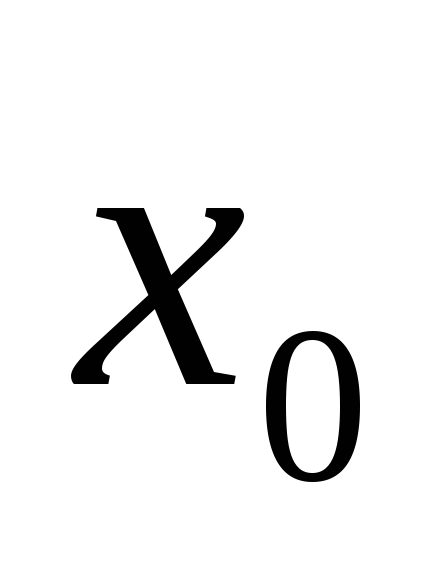приписується індекс 0 (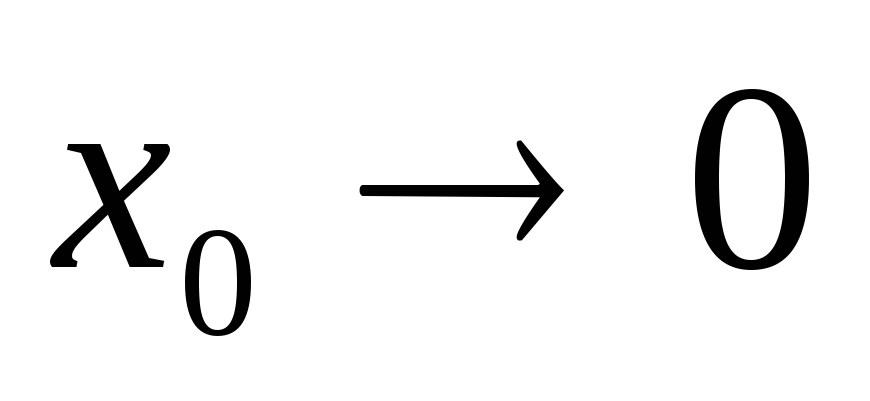), всім іншим вершинам індекси приписуються так:

а) якщо - має індекс

ненасичена дуга

то j -тій вершині приписується індекс

б) якщо - має індекс

ненасичена дуга

то j -тій вершині приписується індекс

Приклад.

,

,

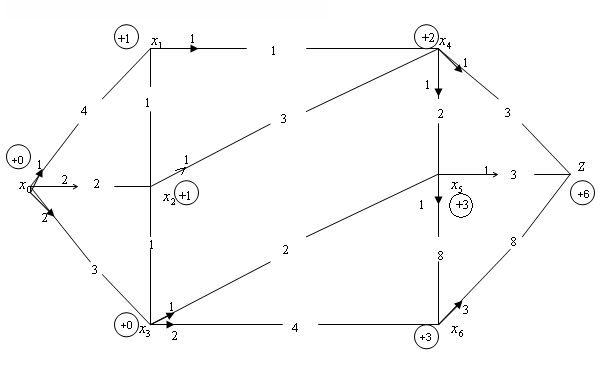
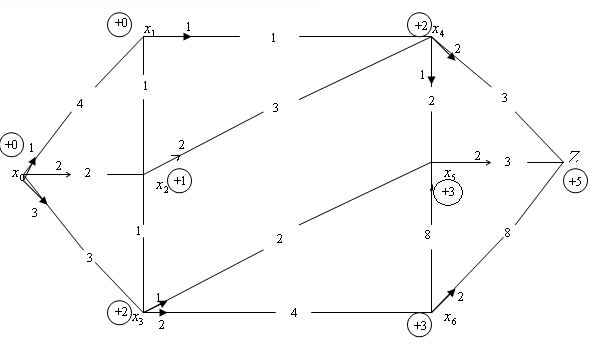
- найбільший потік.

Контрольні запитання.

1. Основні поняття теорії графів.

2. Види графів.

3. Способи задання графів.(*)

4. Означення маршрута, ланцюга, цикла.

5. Означення дерева, бінарного дерева, приклади. (*)

6. Ейлерів граф.

7. Транспортні мережі: пропускна здатність ребра, поняття потоку. (**)

8. Задача про найбільший потік, алгоритм її ров’язання. (***)

Література:

Ю.В. Нікольський, В.В.Пасічник, Ю.М. Щербина. Дискретна математика. Підручник для вищих навчальних закладів. Київ. 2007р. розділ 3. п. 3.1 – 3.9

Розділ 6. Теорія алгоритмів.

План.

1. Поняття алгоритму.

2. Основні вимоги до алгоритмів

3. Властивості алгоритмів.

4. Машина Тьюринга.