
- •Розділ 1. Теорія множин.
- •1. Основні означення теорії множин.
- •2. Дії над множинами.
- •3. Алгебра множин.
- •Розділ 2. Вектори, відношення, відображення.
- •1. Вектори і прямий добуток множин.
- •2. Відношення.
- •Відображення.
- •4. Функції.
- •5. Перетворення.
- •6. Сукупність підстановок множини м: s(м).
- •7. Алгебраїчні операції та системи.
- •Розділ 3. Алгебра логіки.
- •1. Висловлення.
- •2. Основні логічні операції.
- •3. Основні закони алгебри логіки.
- •4. Логічна функція.
- •5. Бульові функції.
- •Розділ 4. Диз’юнктивні та кон’юнктивні нормальні форми.
- •1. Диз’юнктивні нормальні форми.
- •1) Елементарний добуток
- •2) Диз`юнкція різних елементарних добутків відносно
- •3) Тотожна хибність.
- •2. Досконала диз’юнктивна нормальна форма. (дднф)
- •3. Скорочена днф.
- •1. Імпліканта.
- •2. Скорочена днф.
- •4. Мінімізація логічних функцій методом Квайна.
- •5. Кон’юнктивні нормальні форми.
- •6. Мінімізація логічних функцій за допомогою таблиць Вейча.
- •7. Мінімізація неповністю визначених логічних функцій.
- •Розділ 5. Теорія графів.
- •1. Основні поняття.
- •2. Способи задання графів.
- •3. Маршрути, ланцюги, цикли.
- •4. Ейлерів граф.
- •5. Дерево.
- •Чотирикутники
- •6. Транспортні мережі.
- •1. Поняття алгоритму.
- •2.Основні вимоги до алгоритмів.
- •3. Властивості алгоритмів.
- •4. Машина Тьюринга.
2. Дії над множинами.
-
Об’єднанням множин А і В називається множина, яка складається з усіх тих і тільки тих елементів, які належать хоча б одній з множин А або В.
Позначається:
![]()
Об’єднання
множин можна виконувати з будь – якою
кількістю множин:
![]()
Для об’єднання множин справедливі слідуючи властивості:
-
комутативна:

-
асоціативна:
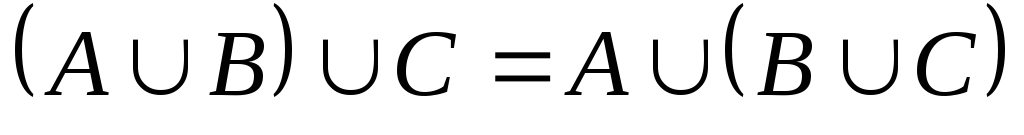
-
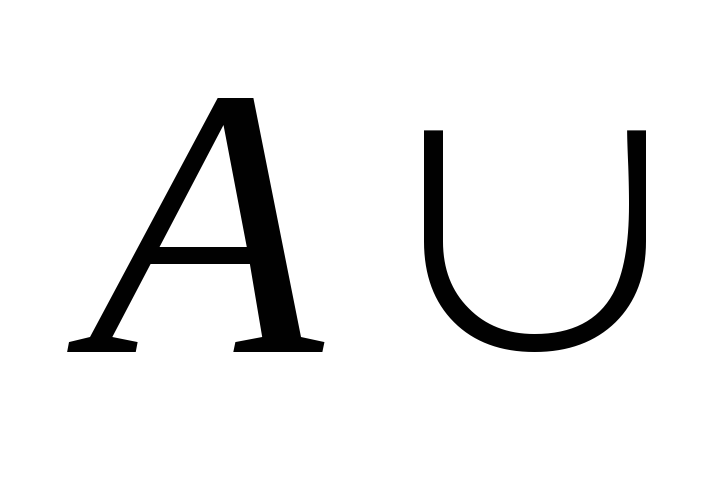 =А
=А -
ідемпотентність:

-
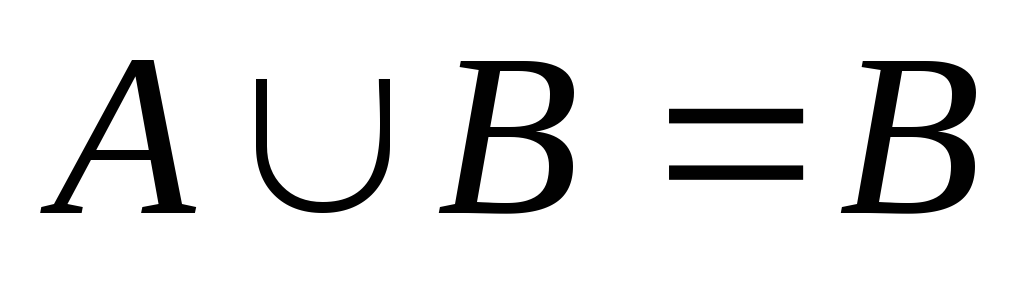 тоді
і тільки тоді, коли
тоді
і тільки тоді, коли

Діаграми (круги) Ейлера – Венна - це графічне зображення множин.
(Д. Венн – англійський математик, 1834-1932р.р. Л. Ейлер – швейцарський математик, 1707-1783р.р.)


Приклад:
![]()
-
Перетином множин А і В називається множина, яка складається з усіх тих і тільки тих елементів, які належать як множині А так і множині В (спільні елементи множин).
Позначається:
![]()
Дві
множини А
і В
називаються непересічними,
якщо
![]() .
.
Дві
множини А
і
В
називаються
пересічними,
якщо
![]() .
.
Перетин
множин можна виконувати з будь – якою
кількістю множин:
![]()
Для перетину множин справедливі слідуючи властивості:
-
комутативна:
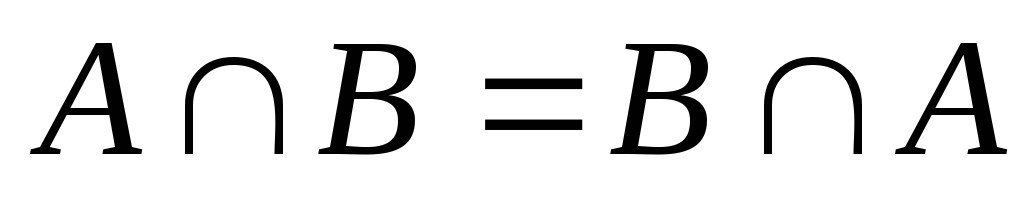
-
асоціативна:
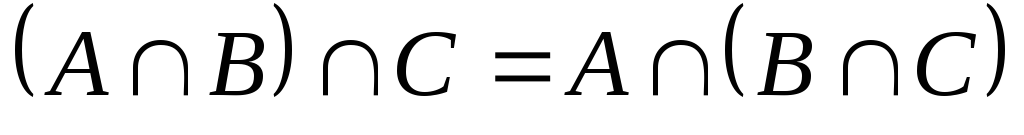
-
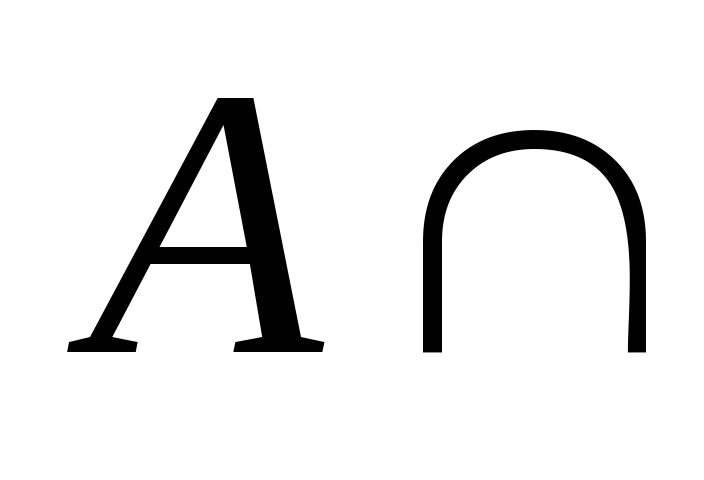 =
= -
ідемпотентність:

-
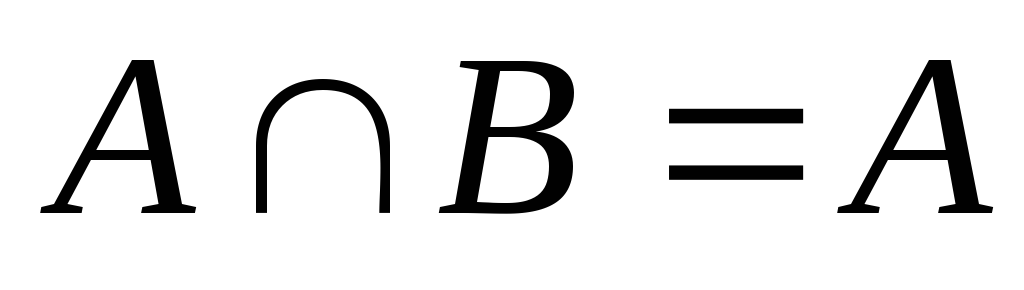 тоді
і тільки тоді, коли
тоді
і тільки тоді, коли

Приклад:
![]()
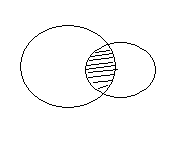
-
Різницею множин А і В називається множина, яка складається з тих і тільки тих елементів, які належать множині А і не належать множині В.
Позначається:
![]()


![]()
![]()
Множина
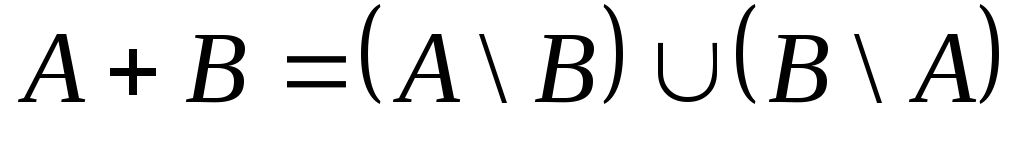
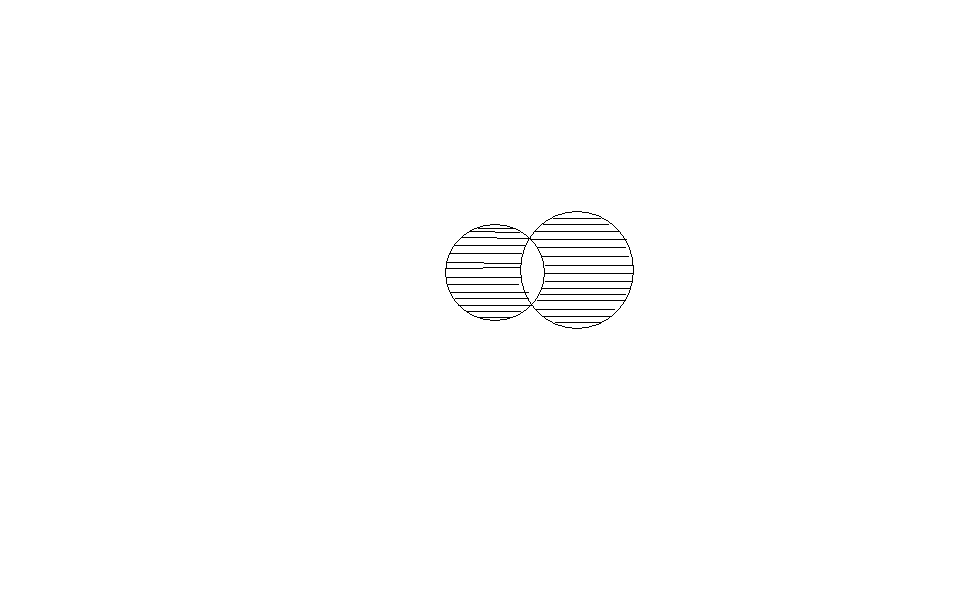
Приклад
:
![]()
-
Універсальна множина – це найбільша множина U, для якої вся решта множин є підмножинами.
На діаграмах Ейлера – Венна універсальну множину позначають прямокутником:

Для
універсальних множин справедливі
слідуючи співвідношення:
![]() ,
,
![]()
-
Доповненням множини А до універсальної множини U називається така множина, що визначається співвідношенням
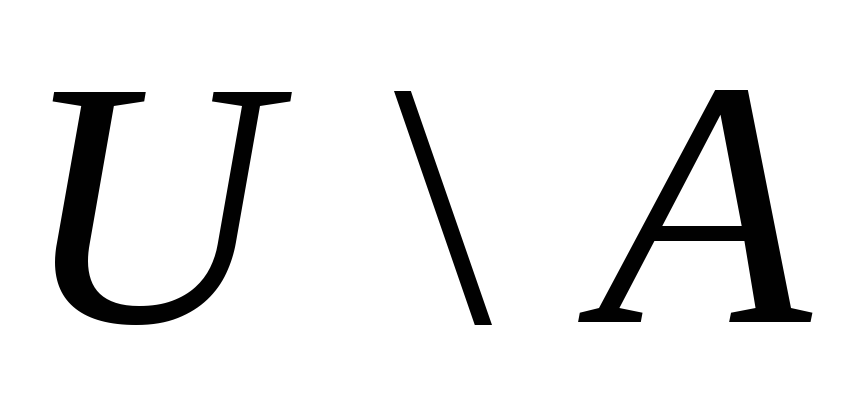
Позначається:
![]()
Множини
![]() і
і
![]() не мають спільних елементів, тому
не мають спільних елементів, тому
![]() ,
,
![]() .
Очевидно, що множина А є доповненням до
.
Очевидно, що множина А є доповненням до
![]() ,
а тому
,
а тому
![]() .
.
За
допомогою доповнення множин можна також
у зручному вигляді подати різницю множин
![]() .
.
Теорема:
![]()
Доведення:
так як
![]() ,
то
,
то
![]() .
.
3. Алгебра множин.
Алгебра множин являє собою сукупність тотожностей (рівностей).
Для будь – яких підмножин А, В і С універсальної множини U дійсними є такі рівності:
-
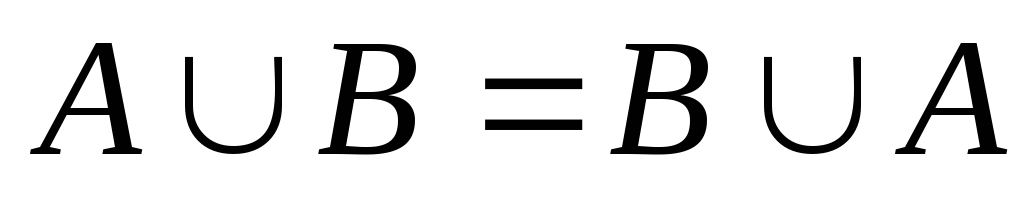 -
комутативний закон
-
комутативний закон -
 -
асоціативний закон
-
асоціативний закон -
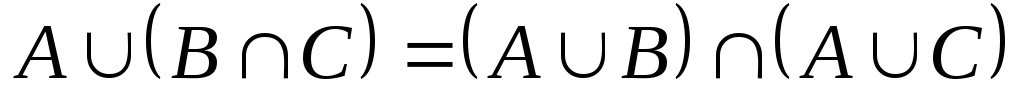 -
дистрибутивний закон
-
дистрибутивний закон -
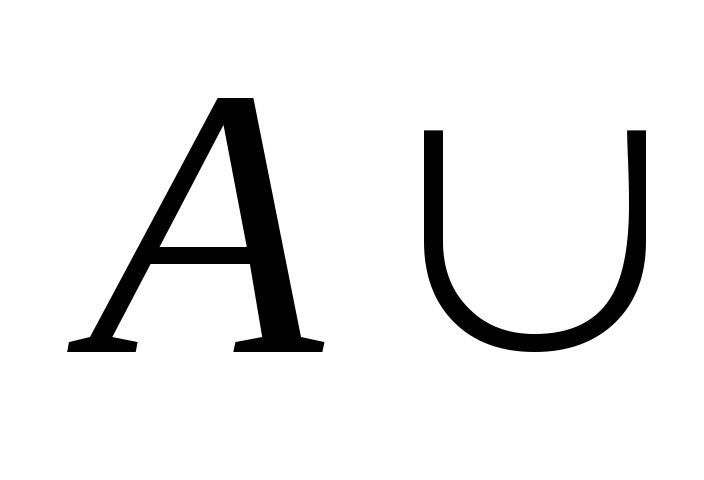 =А
=А -
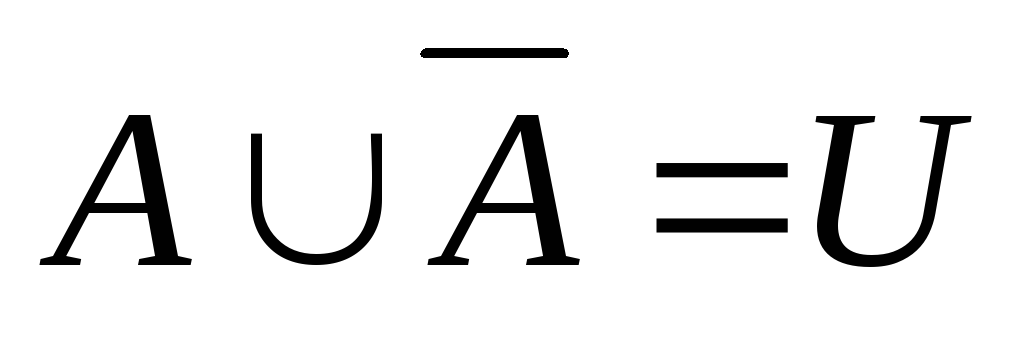 (
(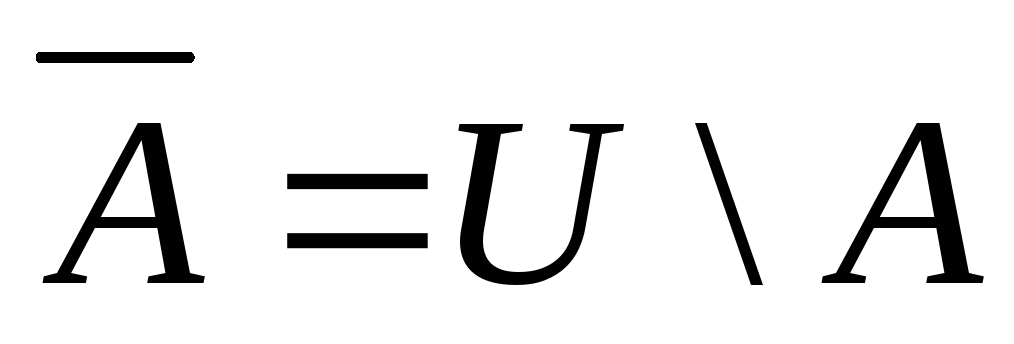 )
)
1’)
![]() - комутативний закон
- комутативний закон
2’)
![]() - асоціативний закон
- асоціативний закон
3’)
![]() - дистрибутивний закон
- дистрибутивний закон
4’)
![]()
5’)
![]()
Кожну з наведених рівностей можна довести, показавши, що множина, яка стоїть з одного боку знака рівності, включена до множини, що стоїть з іншого боку від цього знака рівності.
Доведемо
рівність 3:
![]()
Доведення складається з двох частин:
-
Нехай
 ,
тоді
,
тоді
 або
або

а)
якщо
![]() ,
то
,
то
![]() і
і
![]() ,
а отже
,
а отже
![]()
б)
якщо
![]() ,
то
,
то
![]() і
і
![]() ,
а отже
,
а отже
![]() і
і
![]() ,
тому
,
тому
![]()
-
Нехай
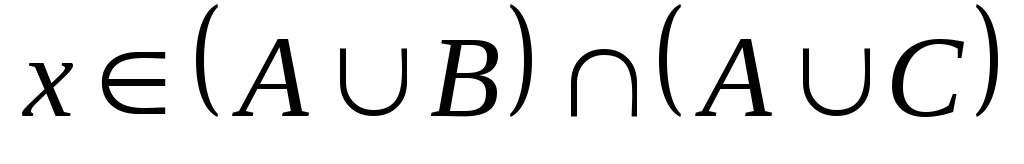 ,
тоді
,
тоді
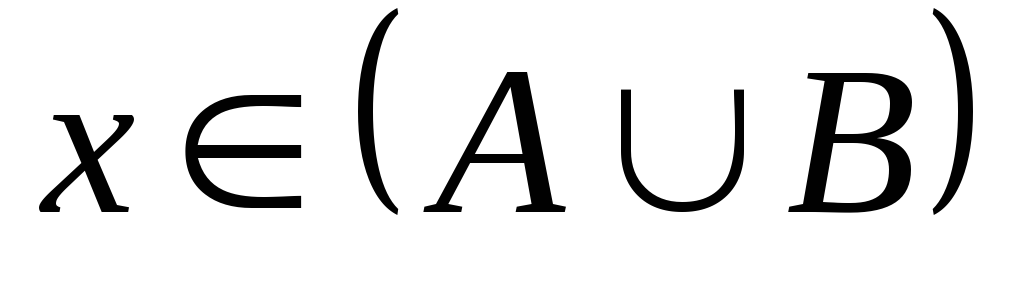 і
і
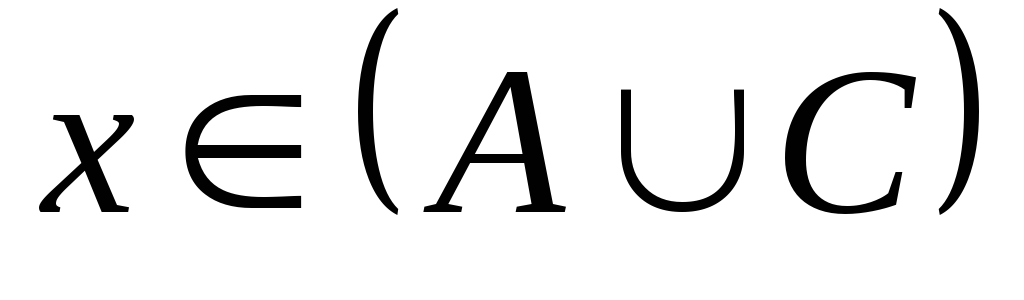 ,
тому
,
тому
 або
(
або
(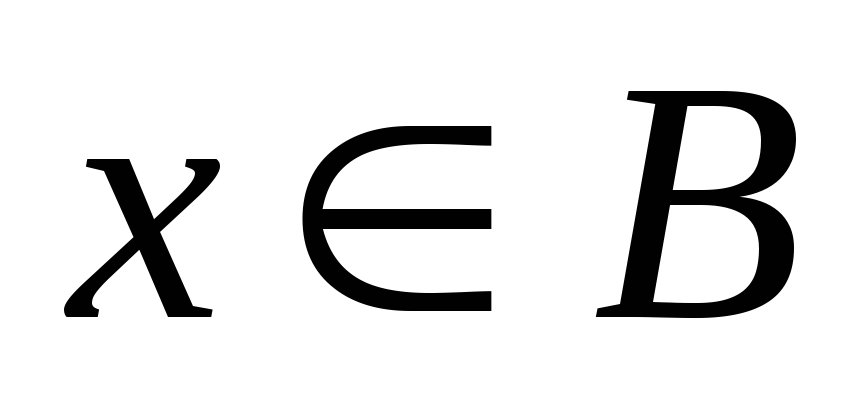 і
і
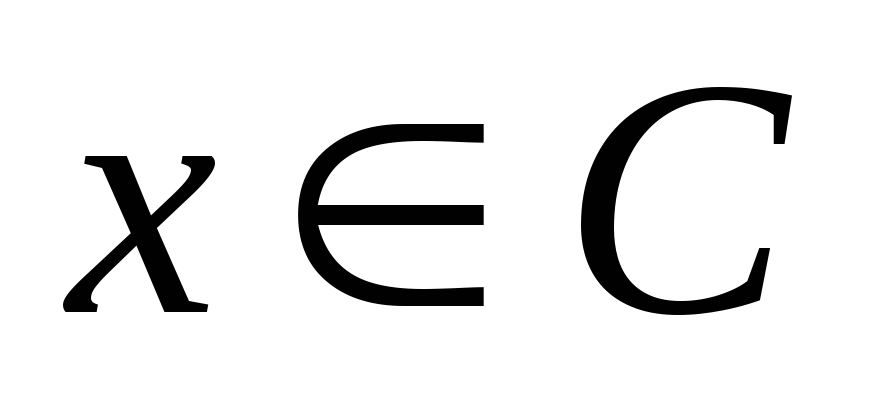 ),
а значить
),
а значить
 .
.
У загальному вигляді рівності 3 і 3’ можна подати у такому вигляді:
![]()
![]()
Для довільних підмножин А, В універсальної множини U справедливі такі рівності:
-
якщо
 і
і
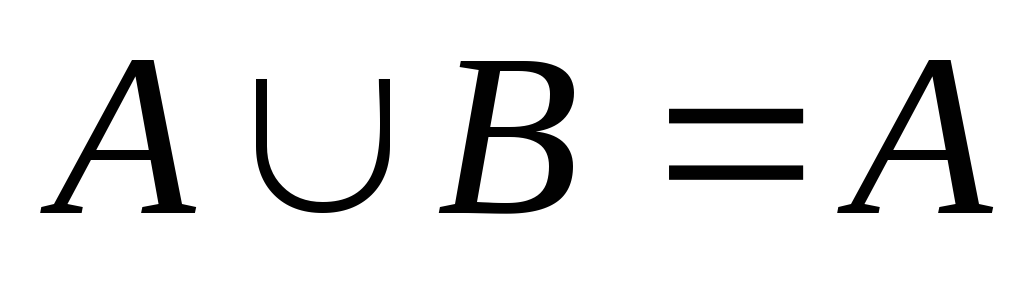 ,
то В=.
,
то В=. -
 =U
=U -
 -
закон ідемпотентності
-
закон ідемпотентності -
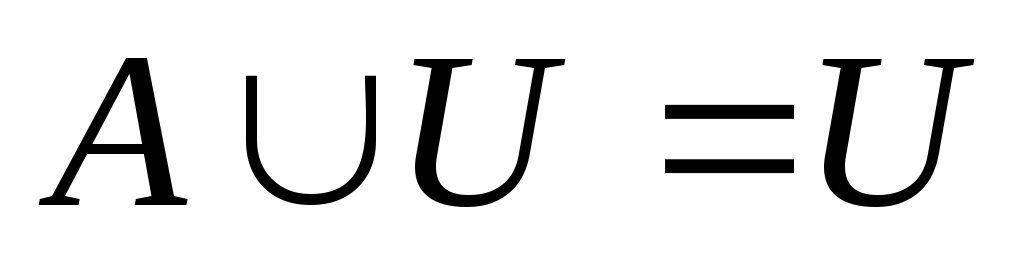
-
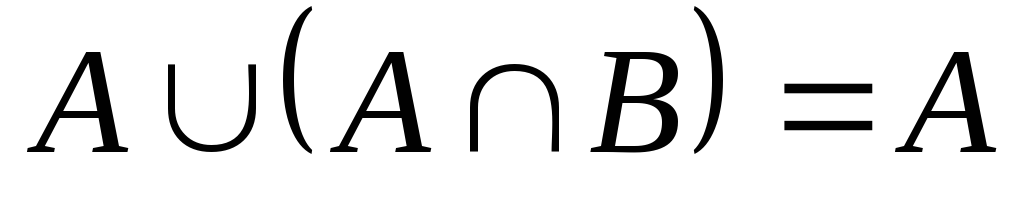 -
закон поглинання
-
закон поглинання -
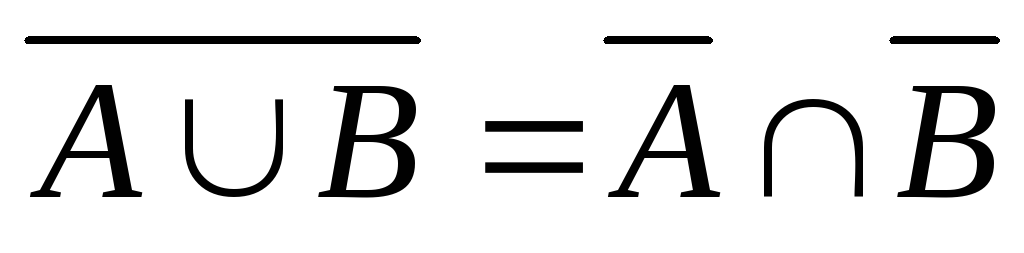 -
закон
де
Моргана
-
закон
де
Моргана -
якщо
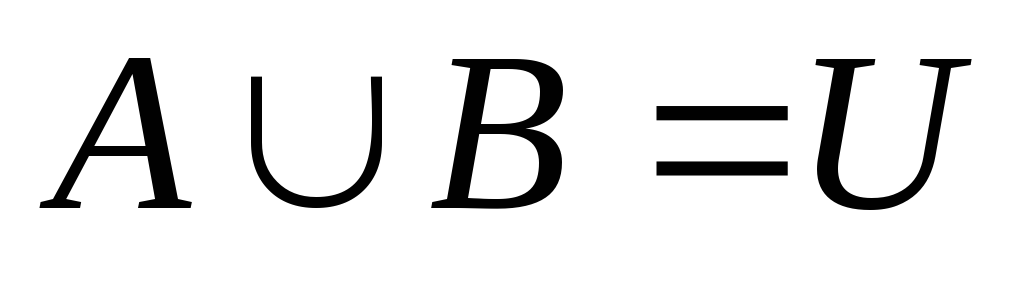 і
і
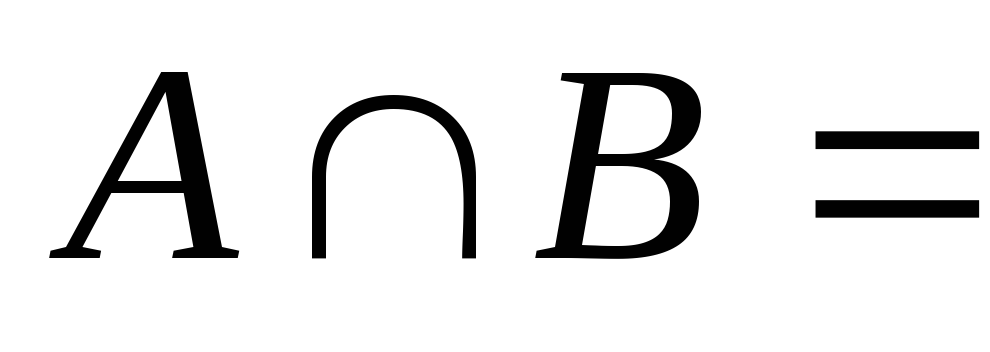 ,
то
,
то
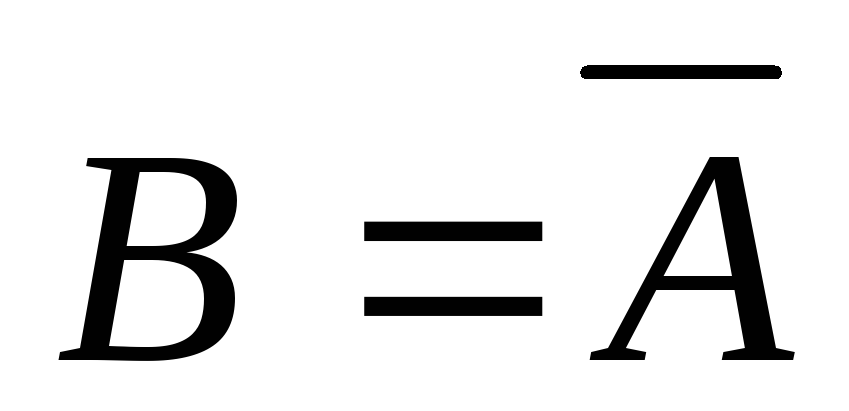
1’)
якщо
![]() і
і
![]() ,
то
,
то
![]() .
.
2’)
![]()
3’)
![]() -
закон ідемпотентності
-
закон ідемпотентності
4’)
![]() =
=
5’)
![]() -
закон поглинання
-
закон поглинання
6’)
![]() - закон
де
Моргана
- закон
де
Моргана
7’)
якщо
![]()
![]() і
і
![]() ,
то
,
то
![]()
Рівність
алгебри множин, отримана з іншої рівності
через заміну всіх входжень
![]() ,
,
![]() ,
,
![]() на
,
на
на
,
на
![]() називається двоїстою по відношенню до
вихідної рівності.
називається двоїстою по відношенню до
вихідної рівності.
Для
будь – якого істинного твердження , що
формується в термінах
![]() та
та
двоїсте по відношенню до цього речення є також істинним. З цього випливає, що якщо є деяке твердження 1 – 7, то відповідне йому твердження 1’ – 7’ випливає на підставі двоїстості. Це дозволяє спрощувати різні складні вирази алгебри множин.
Узагальнення операцій над множинами:
-
перетин множин:
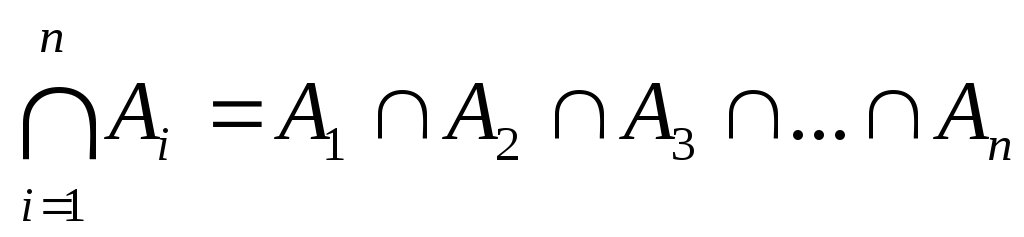 при
при
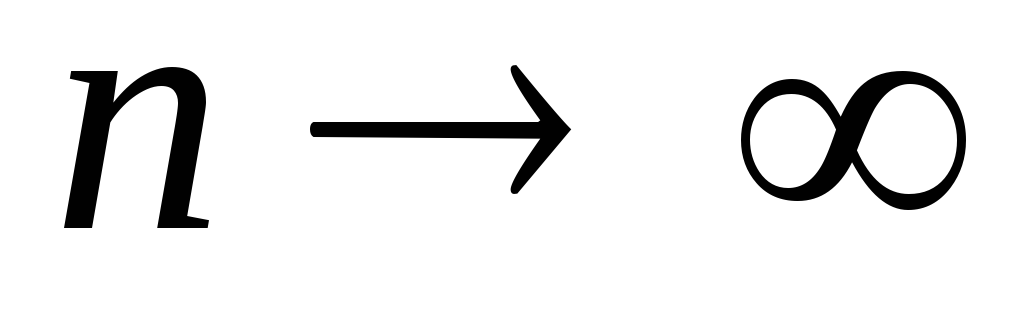 ;
; -
об’єднання множин:
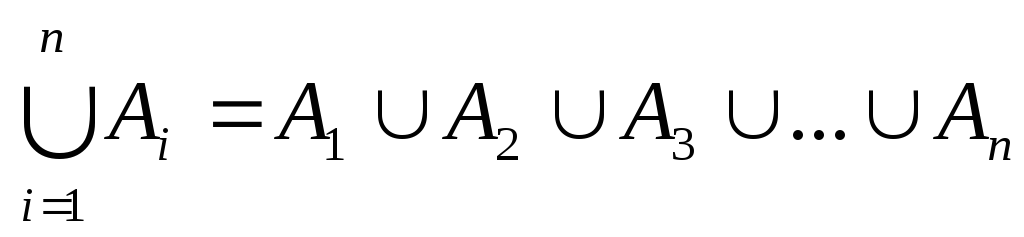 при
при
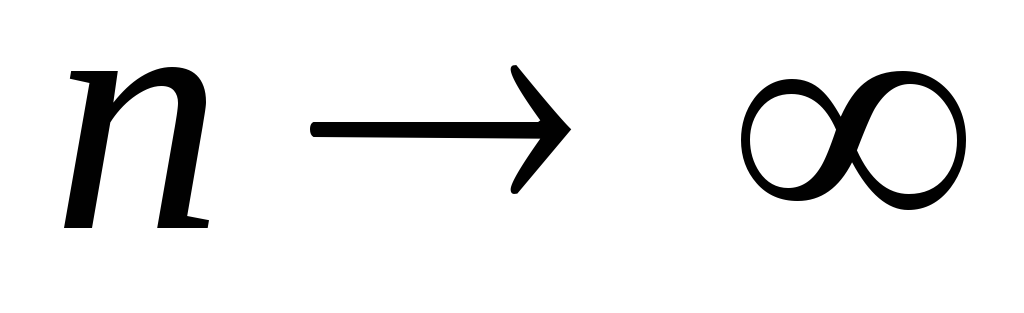 ;
; -
формули де Моргана:
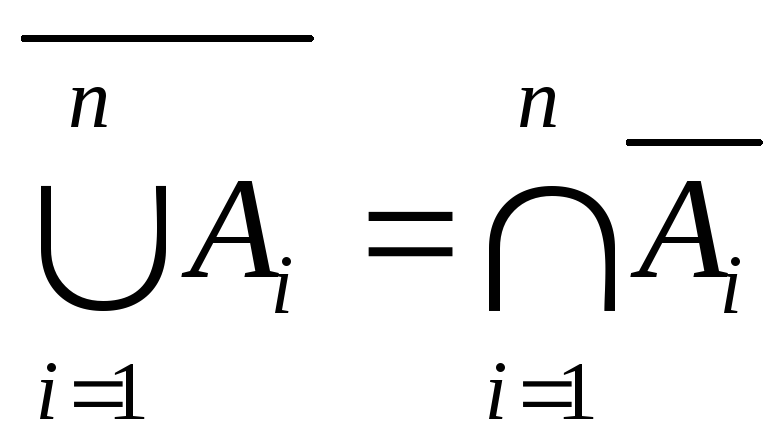 ,
,
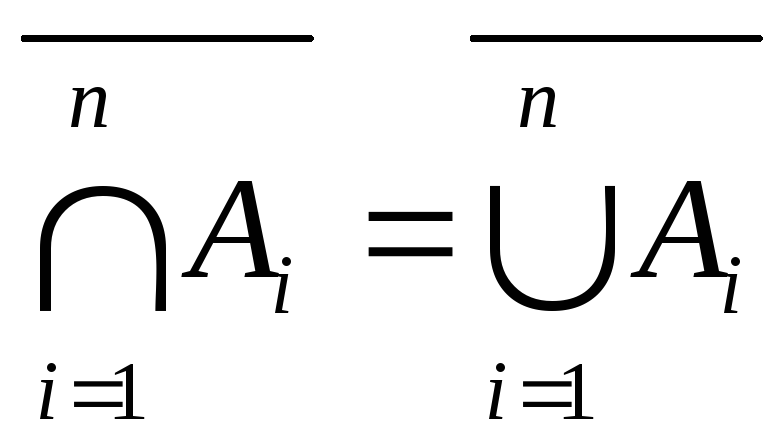 .
.
Контрольні запитання.
-
Що таке множина? Наведіть приклади різних множин.
-
Що таке скінченна та нескінченна множини? Наведіть приклади.
-
Яка множина називається порожньою?
-
Що таке підмножина?
-
Які є способи задання множин?
-
Що називається потужністю множини?
-
Що називається булеаном множини?
-
Що називається об’єднанням множин? (*)
-
Що називається об’єднанням множин? (*)
-
Що називається перерізом множин? (*)
-
Що називається різницею множин? (*)
-
Сформулювати і записати закони алгебри множин. (**)
Література:
О.А. Борисенко. Лекції з дискретної математики: навчальний посібник для вузів. Суми, СумДУ, 1999р. лекції 2 - 4
Ю.В. Нікольський, В.В.Пасічник, Ю.М. Щербина. Дискретна математика. Підручник для вищих навчальних закладів. Київ. 2007р. розділ 1. п. 1.12 – 1.13
