3. Скорочена днф.

ДДНФ є найбільш загальною формою подання логічних функцій в диз`юктивній нормальній формі і тому містить найбільш можливе число літер.

Число літер, що входять до ДНФ логічної функції дорівнює або більше числа змінних, які містяться в цій функції оскільки одна і та сама змінна може входити до функції кілька разів.

Наприклад: ДНФ(F)=

Містить 6 літер (а змінних 3) внаслідок того, що А - входить до функції двічі, В -тричі.

На практиці і відповідно в теорії постає проблема скорочення числа літер у ДДНФ.

1. Імпліканта.

Застосування терміну імпліканта пов’язане з логічною функцією F=, яку ще ще називають імплікацією.

Вираз дорівнює одиниці лише тоді, коли , тобто на наборах де значення відповідно мають вигляд 0-0; 0-1; 1-1.

1 0 0	1 1 0	1 1 1
1	0	0

Якщо деяка логічна функція на тих наборах на яких інша функція F=0, то називається імплікантою F. При цьому може дорівнювати 0 і на тих наборах на яких F=1. (але не навпаки).

- будь-яка конституента одиниці, що входить до ДДНФ логічної функції F, є її імплікантою.

- константа нуля є імплікантою будь-якої логічної функції.

Доведення: Дійсно константа нуля („F=0”) за означенням дорівнює 0 на всіх її можливих наборах і тому обов’язково дорівнює 0 на всіх тих наборах, на яких функція F дорівнює нулю.

- будь-яка логічна функція є імплікантою самої себе.

- будь-яка логічна функція є імплікантою константи одиниці.

2. Скорочена днф.

Елементарний добуток, одержаний шляхом виключення з початкового добутку

однієї або кількох змінних, називається власною частиною добутку.

Приклад: Власними частинами цього добутку будуть:

Елементарні добутки, які входять до даної функції в ДДНФ, але ніяка їх власна час­тина самостійно, як добуток не входить, називаються простими імплікантами.

Приклад: Нехай добутки , а змінні і самостійно не входять як добутки. Тоді добуток буде простою імплікантою функції F, бо , а . Але добуток не буде простою імплікантою, бо її власна частина .

Прикладом такої функції буде

Диз’юнкція простих імплікант називається скороченою ДНФ.

Для того, щоб подати логічну функцію у вигляді скороченої ДНФ використовують слідуючи операції:

1. Операція повного склеювання:

(склеювання добутків відбувається по змінній х)

2. Операція неповного склеювання:

(додавання х ніяк не впливає початковий вираз)

3. Операція поглинання:

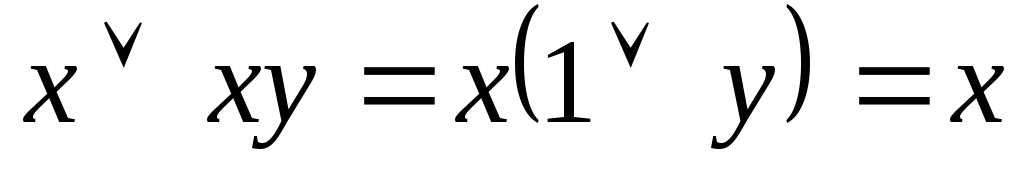
(х поглинає весь вираз)

Операція розгортання: для простої імпліканти функції трьох змінних , то

Оскільки далеко не завжди вихідна логічна функція подається у ДДНФ, то розгля­дають операцію її розгортання. Вона перетворює будь-яку просту імпліканту в диз’юнкцію конституент одиниці. При розгортанні різні імпліканти можуть утворювати одну й ту саму конституенту одиниці. У цьому разі на основі тотожності залишають одну. Після цього одержимо ДДНФ вихідної логічної функції.