1) Елементарний добуток

2) Диз`юнкція різних елементарних добутків відносно

3) Тотожна хибність.

Для кожної формули алгебри висловлень існує ДНФ, яка може бути знайдена за допомогою скінченого числа дій.

Алгоритм зведення логічної формули до ДНФ:

1) зводимо до трьох основних операцій: ¯ ;

2) якщо є добутки диз’юнкції, то застосовують дистрибутивні закони:

3) на підставі закону тавтології викреслюємо повторні множники або зайві додатки, а також додатки типу (на основі закону суперечності).

Після таких скорочень залишається або елементарний добуток або диз’юнкція різних елементарних добутків відносно або нічого, бо все скоротиться.

Звести до ДНФ:

а)

= =

б) =

= - тотожна хибніст

в)

2. Досконала диз’юнктивна нормальна форма. (дднф)

Конституентою одиниці основних висловлень називається повний елементарний добуток, який містить усі букви

Конституента одиниці відносно є добутком n множників, кожен з яких дорівнює або (тобто кожне з основних висловлень входить в цей добуток).

Всі множники конституенти одиниці позначаються різними буквами.

Для двох висловлень і можна утворити чотири конституенти одиниці: , , , .

Для трьох висловлень отримуємо вісім конституент одиниці:

;

=;

;

;

;

;

;

Кожна конституента одиниці істинна на одному і тільки одному наборі. Між конституентами одиниці для і n-місними наборами існує взаємно-однозначна відповідність:

- кожній конституенті одиниці відповідає єдиний набір на якому вона істинна;

- кожен набір відповідає єдиній конституенті одиниці.

Наприклад:

1)

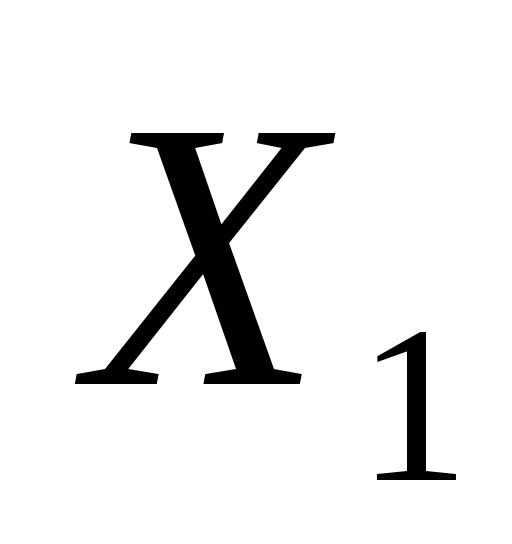
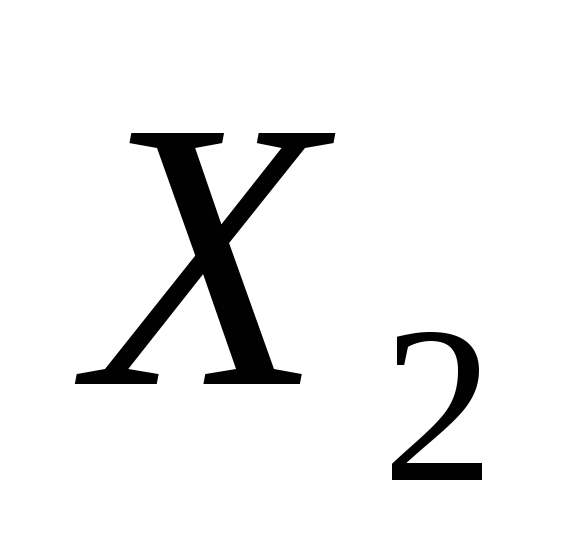
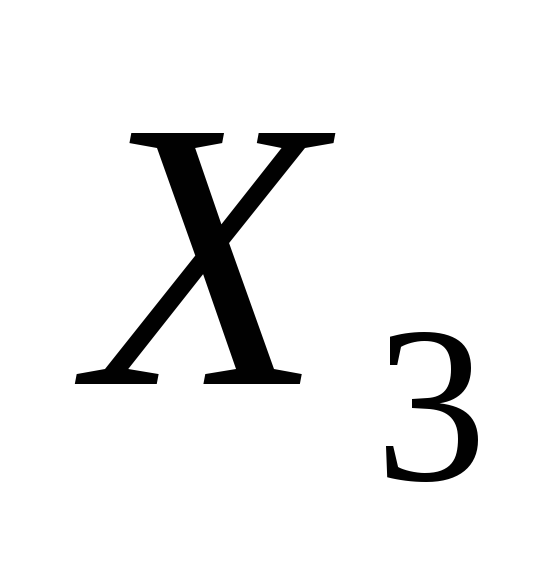
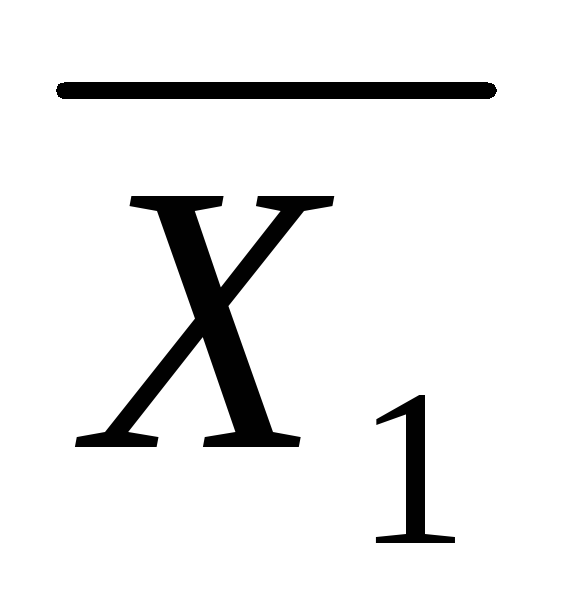
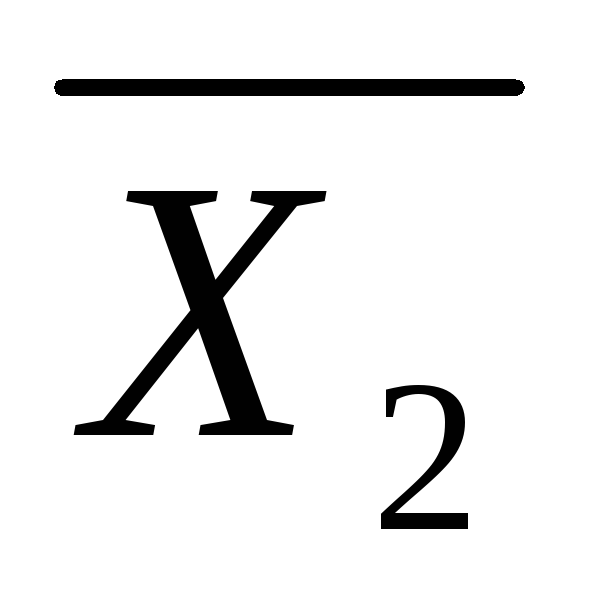
1 1 1 1 0 0 0 0	1 1 0 0 1 0 1 0	1 0 0 1 1 1 0 0	0 0 0 0 1 1 1 1	0 0 1 1 0 1 0 1	0 0 0 0 0 1 0 0

=1 на наборі 001, на всіх інших наборах вона хибна

2) -істинна на наборі 100

Висновки:

1) число конституент одиниці відносно дорівнює числу -місних наборів: 2ⁿ

для : 2² = 4 конституенти

для : 2³ = 8 конституент

2) якщо на якомусь наборі істинна, то на цьому наборі всі інші конституенти хибні. =1 на наборі 001 на цьому наборі.

Конституенти одиниці для двох змінних: n=2.

Набори			Конституенти одиниці
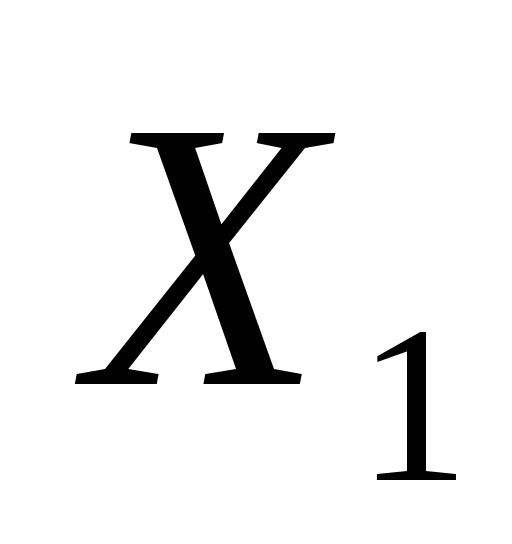
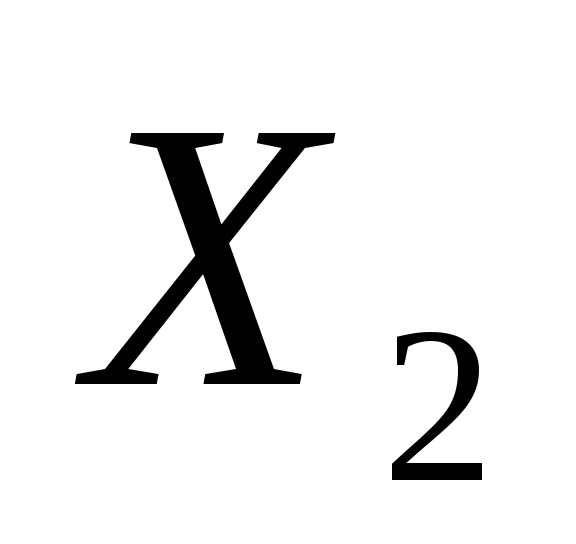
N0 N1 N2 N3	0 0 1 1	0 1 0 1

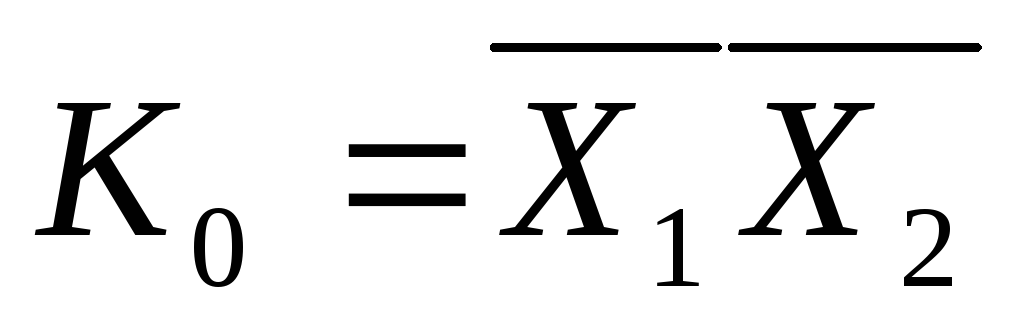
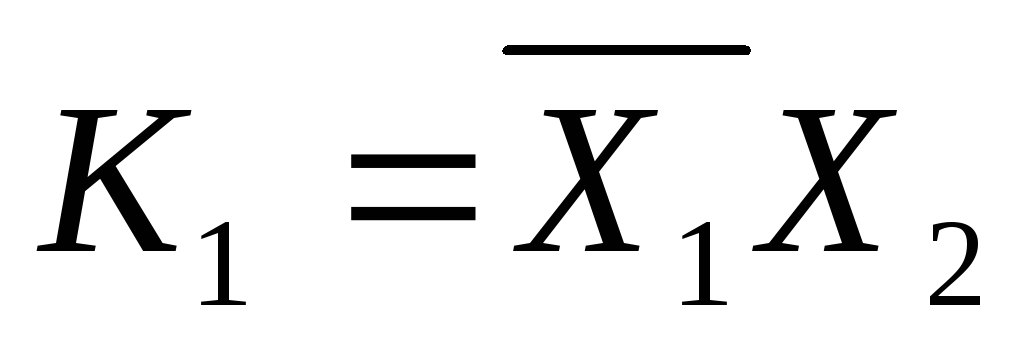
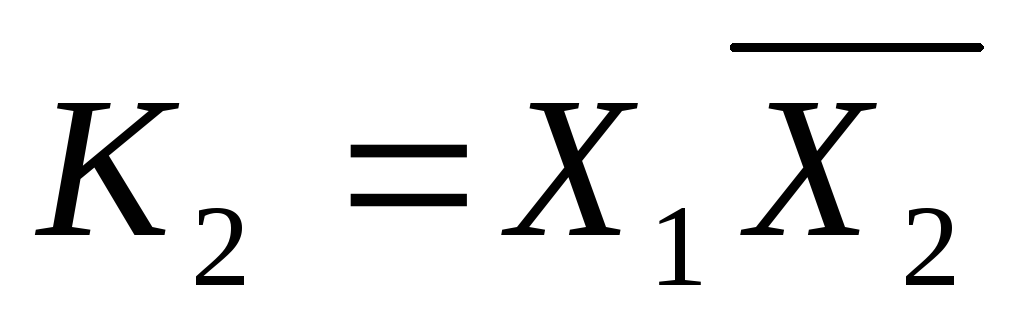
Конституенти одиниці для трьох змінних: n=3.

Набори				Конституента одиниці
N0 N1 N2 N3 N4 N5 N6 N7	0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1

Диз`юнктивна нормальна форма називається досконалою, якщо всі її доданки є конституентами одиниці.

Теорема: Якщо формула алгебри висловлень здійсненна, то для неї існує ДДНФ і вона може бути знайдена за допомогою скінченного числа дій.

Щоб отримати ДДНФ треба:

- якщо в „неповний ” елементарний добуток не входить , то домножимо його на =1

- розкривають дужки за першим дистрибутивним законом , у цьому разі дістають диз`юнкцію елементарних добутків з усіма попередніми буквами і ще однією . (Якщо знову не всі букви охоплені, то знову помножають на і знову розкривають дужки)

- після цього повторні доданки видаляють.

Приклад:

Область істинності: здійсненої формули складається з наборів що відповідають конституентам одиниці, які входять в ДДНФ.

Область хибності знаходять виключивши з усіх можливих наборів область істинності.

=...=

Область істинності: 010;111;110;000;101.

Область хибності: 011;100;001.