5. Бульові функції.

Якщо взяти будь-яку формулу алгебри висловлень, то її значення істинності буде функцією значень істинності простих висловлень з яких вона складається. Ця функція має властивість: вона сама і її аргументи набувають лише двох значень 0 і 1. Такі функції називаються двозначними або бульовими функціями.

Назва дана в честь англійського математика дев’ятнадцятого століття Джорджа Буля, що заклав основи бульової алгебри.

Область значень бульової функції і її аргументів складається з двох елементів: істинності і хибності, а область існування (визначення) – з n-місних наборів.

Приклади бульових функцій в науці і практиці:

• це фізичні системи, які діють за принципом „так – ні ”. Простими елементами таких систем є вимикачі, перемикачі, електричні і електронні лампи, кожен з яких може бути в двох стійких положеннях або станах. В таких же станах може бути і вся система залежно від стану її елементів.

Отже значення бульової функції і її аргументів найрізноманітніші:

- істинність – хибність;

- так – ні;

- струм проходить – не проходить;

- лампа горить – не горить і т. д.

Аргументи бульової функції називаються бульовими змінними.

Різниця між бульовими функціями і алгеброю висловлень:

- алгебра висловлень розглядає тільки функції істинності висловлень, тобто обме жена чисто логічним матеріалом;

- теорія бульових функцій відкидає обмеженість і виходить на широкий простір будь-яких двозначних зв’язків між будь-якими предметами (об’єктами);

- закони теорії бульових функцій мають більш загальний характер і знаходять

більше застосувань в науці і практиці;

- теорія бульових функцій вийшла за межі чистої логіки.

Алгебра висловлень – це лише одна з галузей теорії бульових функцій.

Теорія бульових функцій застосовується в:

- релейно-контактних схемах;

- дискретних автоматах;

- електронно-цифрових обчислювальних машинах;

- деяких питаннях математики.

Бульова алгебра – це множина бульових функцій, які розглядаються разом з трьома основними операціями:

- кон’юнкцією;

- диз’юнкцією;

- запереченням.

Ці операції називаються бульовими, а формули бульової алгебри – бульовими формулами.

Основні формули бульової алгебри:

№ п/п	Формули для диз’юнкцій	Формули для кон’юнкцій	Формули для заперечень
1 2 3 4 5 6 7 8 9

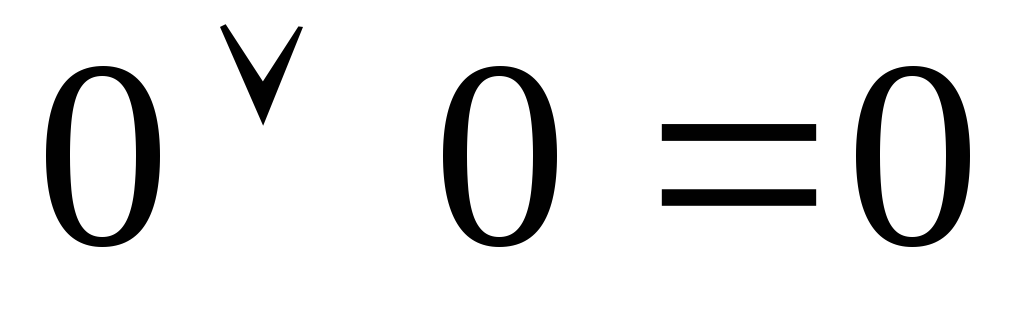
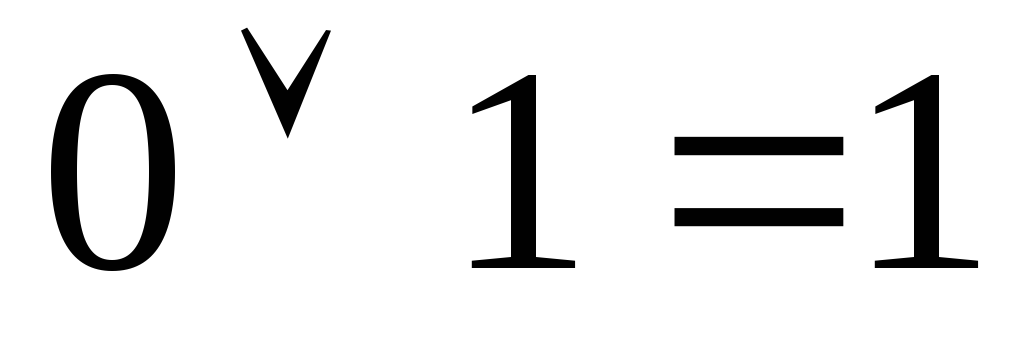
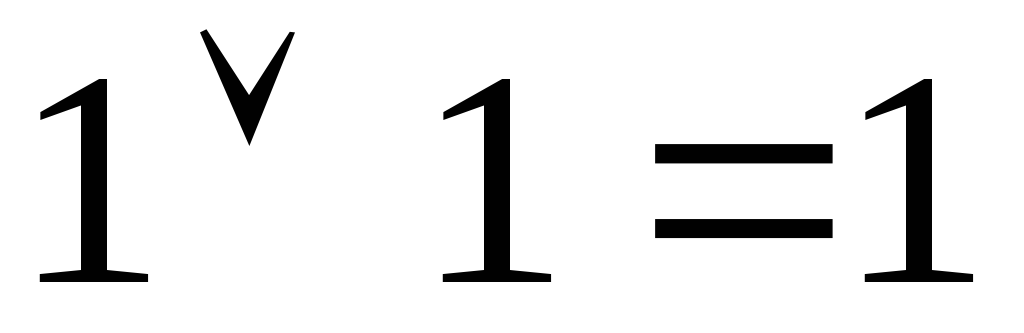
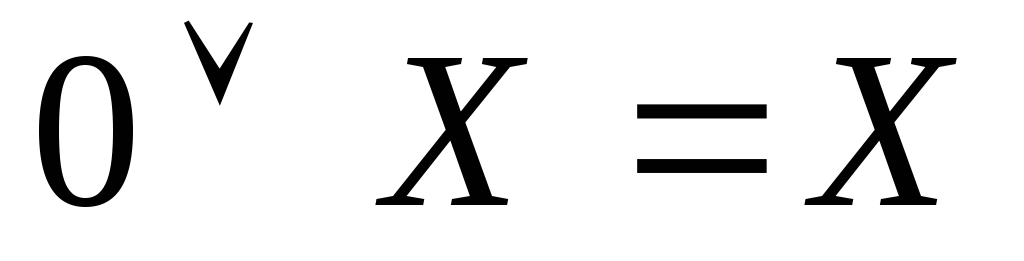
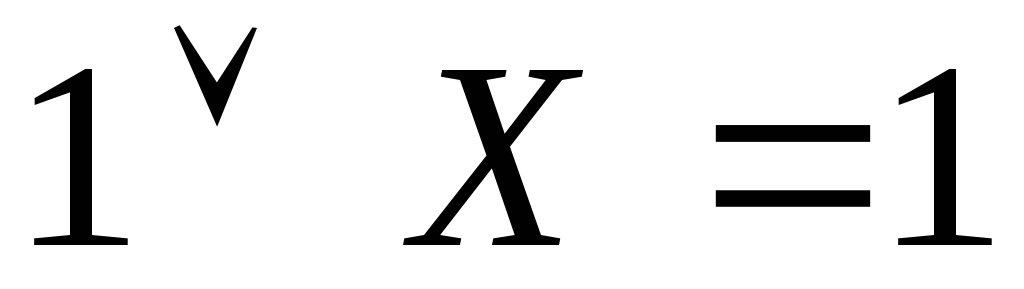
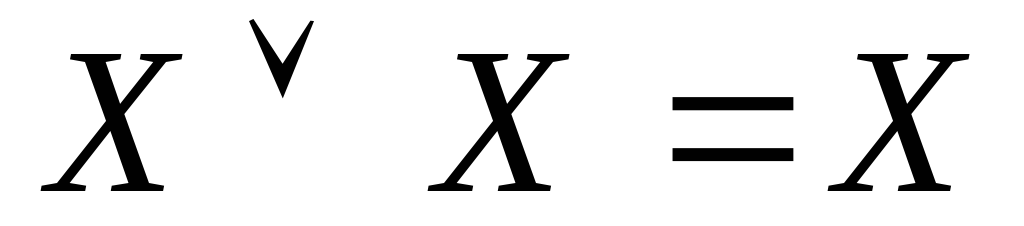
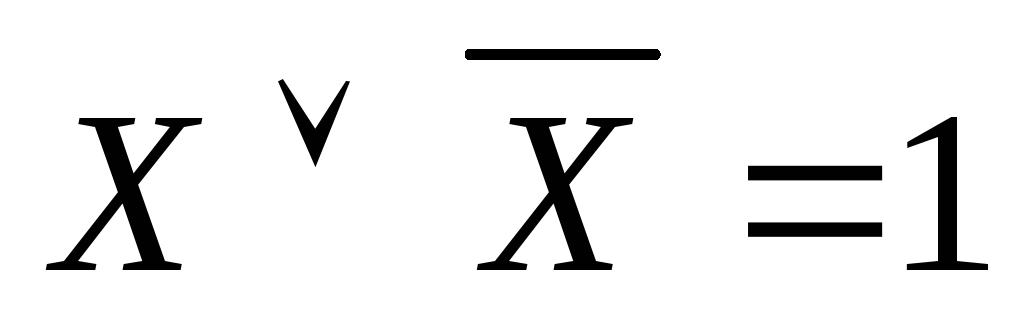
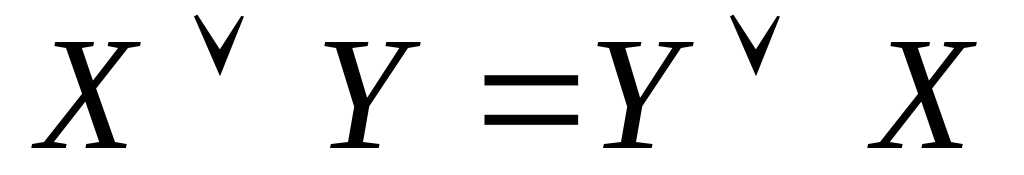
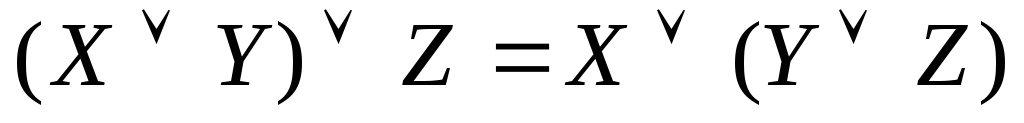
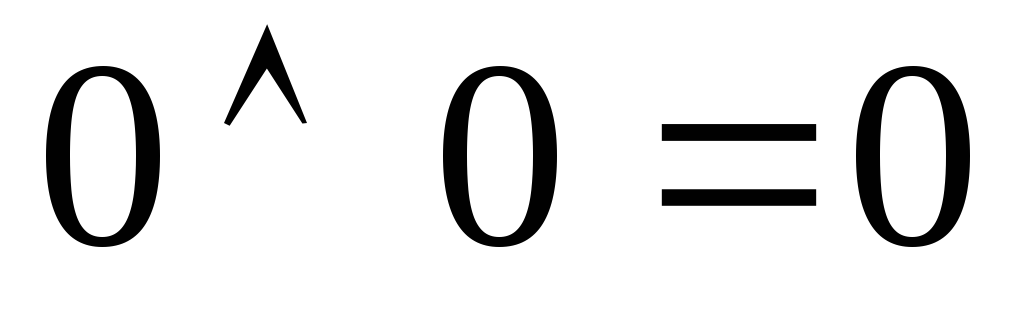
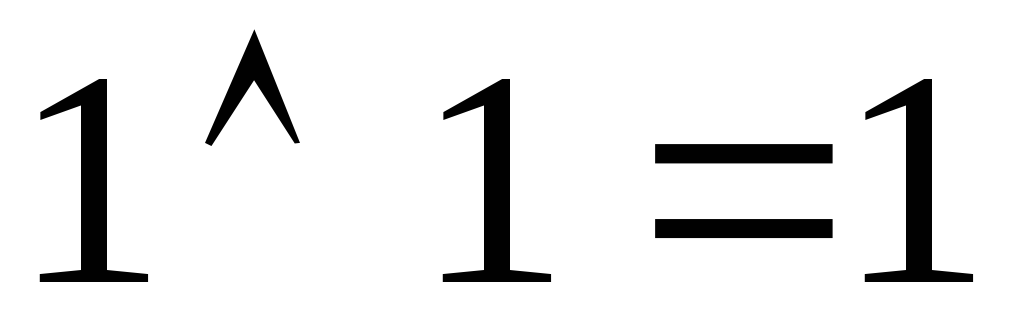
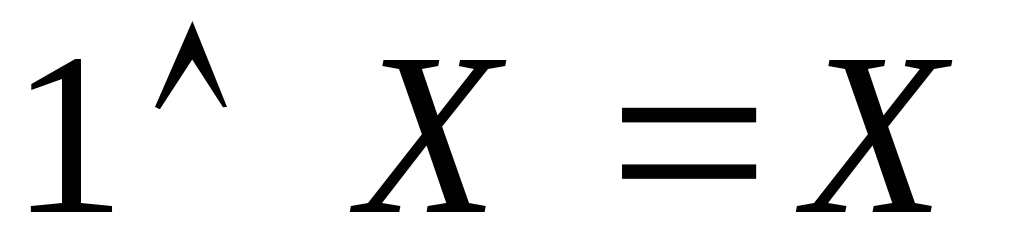
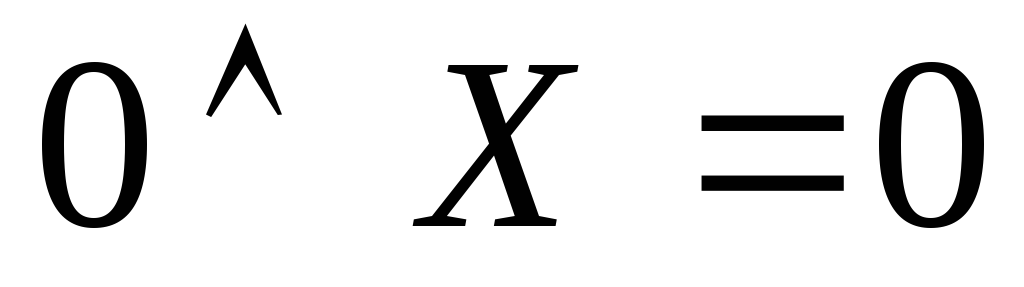
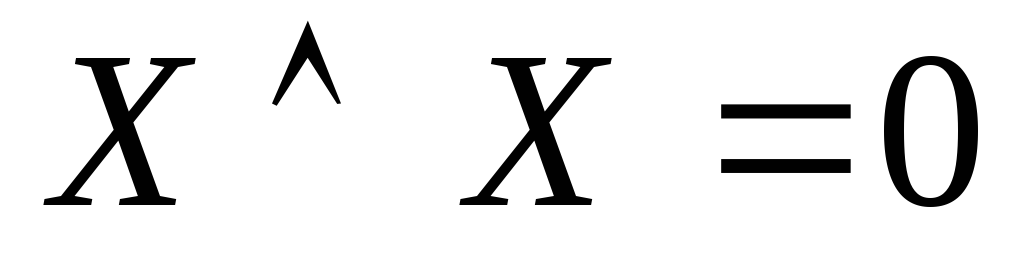
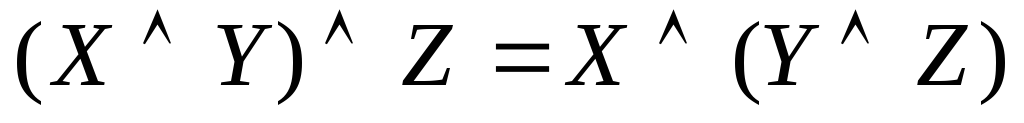
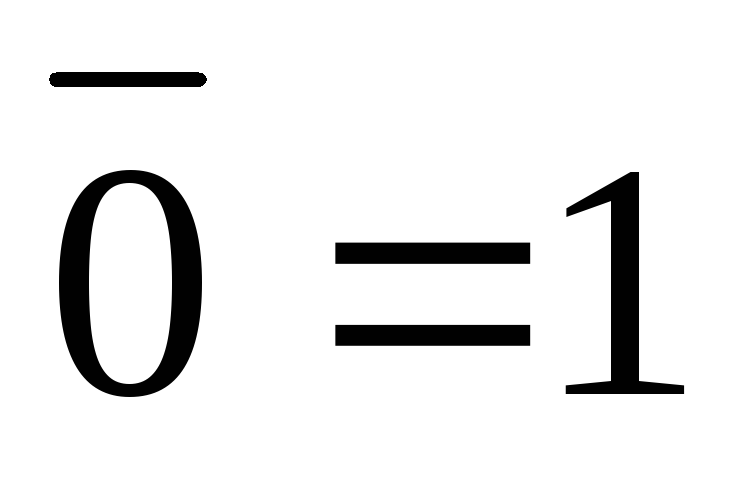
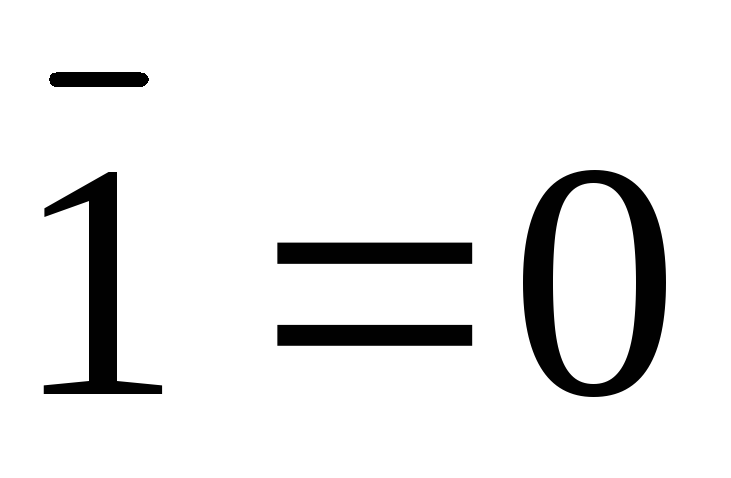
Спеціальні формули бульової алгебри:

(закон контрапозиції).

Контрольні запитання.

1. Що таке математична логіка?

2. Що називається висловленням? Наведіть приклади.

3. Яке висловлення називається простим , складним? Наведіть приклади

4. Сформулювати означення основних логічних операцій, їх таблиці істинності.(*)

5. Що називається логічним законом?

6. Що називається логічною суперечністю?

7. Що називається твердженням, що логічно виконується?

8. Назвати та записати основні закони алгебри логіки. (**)

9. Яка функція називається логічною?

10. Які функції є базисними?

11. Яка функція називається бульовою?

12. Де застосовується теорія бульових функцій?

13. Записати основні формули бульової алгебри.(*)

Література:

О.А. Борисенко. Лекції з дискретної математики: навчальний посібник для вузів. Суми, СумДУ, 1999р. лекції 11 - 13

Ю.В. Нікольський, В.В.Пасічник, Ю.М. Щербина. Дискретна математика. Підручник для вищих навчальних закладів. Київ. 2007р. розділ 1. п. 1.1 – 1.8

М.М.Швець. Азбука математичної логіки. Київ. 1965р. розділ 1,