
- •Розділ 1. Теорія множин.
- •1. Основні означення теорії множин.
- •2. Дії над множинами.
- •3. Алгебра множин.
- •Розділ 2. Вектори, відношення, відображення.
- •1. Вектори і прямий добуток множин.
- •2. Відношення.
- •Відображення.
- •4. Функції.
- •5. Перетворення.
- •6. Сукупність підстановок множини м: s(м).
- •7. Алгебраїчні операції та системи.
- •Розділ 3. Алгебра логіки.
- •1. Висловлення.
- •2. Основні логічні операції.
- •3. Основні закони алгебри логіки.
- •4. Логічна функція.
- •5. Бульові функції.
- •Розділ 4. Диз’юнктивні та кон’юнктивні нормальні форми.
- •1. Диз’юнктивні нормальні форми.
- •1) Елементарний добуток
- •2) Диз`юнкція різних елементарних добутків відносно
- •3) Тотожна хибність.
- •2. Досконала диз’юнктивна нормальна форма. (дднф)
- •3. Скорочена днф.
- •1. Імпліканта.
- •2. Скорочена днф.
- •4. Мінімізація логічних функцій методом Квайна.
- •5. Кон’юнктивні нормальні форми.
- •6. Мінімізація логічних функцій за допомогою таблиць Вейча.
- •7. Мінімізація неповністю визначених логічних функцій.
- •Розділ 5. Теорія графів.
- •1. Основні поняття.
- •2. Способи задання графів.
- •3. Маршрути, ланцюги, цикли.
- •4. Ейлерів граф.
- •5. Дерево.
- •Чотирикутники
- •6. Транспортні мережі.
- •1. Поняття алгоритму.
- •2.Основні вимоги до алгоритмів.
- •3. Властивості алгоритмів.
- •4. Машина Тьюринга.
 Міністерство
освіти і науки,молоді та спорту України
Міністерство
освіти і науки,молоді та спорту України
Сумський державний університет
Машинобудівний коледж
ОПОРНІ КОНСПЕКТИ
з дисципліни
“Основи дискретної математики ”
для студентів II курсу спеціальності
5.05010101 „Обслуговування програмних систем і комплексів ”
2011 р.
Опорні конспекти розроблені викладачем дисципліни „ Основи дискретної математики ” Вороніною Н.К.
Розглянуто і затверджено кафедрою математичного аналізу і методів оптимізації Сумського державного університету
Протокол № 6 від 20.11.2009р.
Розглянуто і затверджено цикловою комісією природничо - математичних дисциплін
Протокол № 10 від “02” червня 2011 р.
Рецензент: В.Б. Лобода - кандидат фізико – математичних наук, доцент Сумського державного педагогічного університету ім. А.С. Макаренка
Комп’ютерний набір: Вороніна Ю.М.
Зміст.
|
Розділ 1. Теорія множин ……………………………………………………. 1.1 Основні означення теорії множин ………………………………... 1.2 Дії над множинами………………………………………………… 1.3 Алгебра множин………………………………………….….……... Розділ 2. Вектори, відношення, відображення……………………………. 2.1 Вектори і прямий добуток множин……………………………….. 2.2 Відношення…………………………………………………………. 2.3 Відображення………………………………………………………. 2.4 Функції……………………………………………………………… 2.5 Перетворення……………………………………………………….. 2.6 Сукупність підстановок множини М……………………………… 2.7 Алгебраїчні операції та системи………………………………….. Розділ 3. Алгебра логіки……………………………………………………. 3.1 Висловлення ……………………………………………………….. 3.2 Основні логічні операції…………………………………………… 3.3 Основні закони алгебри логіки……………………………………. 3.4 Логічна функція……………………………………………………. 3.5 Бульові функції…………………………………………………….. Розділ 4. Диз’юнктивні та кон’юнктивні нормальні форми …………….. 4.1 Диз’юнктивна нормальна форма………………………………….. 4.2 Досконала диз’юнктивна нормальна форма……………………… 4.3 Скорочена диз’юнктивна нормальна форма……………………… 4.4 Мінімізація логічних функцій методом Квайна………………….. 4.5 Кон’юнктивна нормальна форма………………………………….. 4.6 Мінімізація логічних функцій за допомогою таблиць Вейча…… 4.7 Мінімізація неповністю визначених логічних функцій………….. Розділ 5. Теорія графів………………………………………………………. 5.1 Основні поняття…………………………………………………….. 5.2 Способи задання графів……………………………………………. 5.3 Маршрути, ланцюги, цикли………………………………………... 5.4 Ейлерів граф………………………………………………………… 5.5 Дерево……………………………………………………………….. 5.6 Транспортні мережі………………………………………………… Розділ 6. Теорія алгоритмів. Машина Тьюринга………………………….. 6.1 Поняття алгоритму…………………………………………………. 6.2 Основні вимоги до алгоритмів…………………………………….. 6.3 Властивості алгоритмів……………………………………………. 6.4 Машина Тьюринга………………………………………………….. Розділ 7. Контрольні завдання …………………………………………….. 7.1 Зразки розв’язання………………………………………………….. |
5 5 6 8 11 11 12 14 17 18 19 20 24 24 25 29 29 32 34 34 37 39 40 43 44 46 48 48 49 51 52 53 55 59 59 60 60 61 64 69
|
Рівні засвоєння навчального матеріалу:
-
перший рівень – початковий – відповідь студента при відтворенні навчального матеріалу – елементарна, фрагментарна, зумовлюється початковими уявленнями про предмет вивчення;
-
другий рівень – середній – студент відтворює основний навчальний матеріал, здатний розв’язувати завдання за зразком, володіє елементарними вміннями навчальної діяльності (*);
-
третій рівень – достатній – студент знає істотні ознаки понять, явищ, закономірностей зв’язків між ними, а також самостійно застосовує знання в стандартних ситуаціях, володіє розумовими операціями (аналізом, абстрагуванням, узагальненням тощо), уміє робити висновки, виправляти допущені помилки; відповідь повна, правильна, логічна, обгрунтована, хоча їй бракує власних суджень (**);
-
четвертий рівень – високий – знання студента є глибокими, міцними, узагальненими, системними; студент уміє застосовувати знання творчо, його навчальна діяльність має дослідницький характер, позначена вмінням самостійно оцінювати різноманітні життєві ситуації, явища, факти, виявляє і відстоює особисту позицію (***).
Розділ 1. Теорія множин.
План.
-
Основні означення теорії множин.
-
Дії над множинами.(*)
-
Алгебра множин.(**)
1. Основні означення теорії множин.
Множина – це будь-яке об’єднання відмінних та визначених об’єктів нашої інтуїції або інтелекту, яке розглядається як єдине ціле.
Множина – це сукупність об’єктів, об’єднаних за певною ознакою.
Приклади:
- множина букв алфавіту;
- множина точок на прямій;
- множина двозначних натуральних чисел;
- множина цілих чисел і т.д.
Множини
позначають А,
В, С,
…
![]()
Об’єкти з яких складається множина називаються її елементами: а, в, с, …
Якщо
елемент а
належить множині А,
то позначають:
![]() .
Якщо елемент d
не
належить множині А,
то позначають:
.
Якщо елемент d
не
належить множині А,
то позначають:
![]() .
.
Якщо елементами множини є числа, то її називають числовою:
-
множина натуральних чисел: N
-
множина цілих чисел: Z
-
множина раціональних чисел: Q
-
множина дійсних чисел: R
Множина називається скінченною, якщо вона має скінченну кількість елементів.
Множина називається нескінченною, якщо вона має нескінченну кількість елементів.
Кількість
елементів множини називається потужністю:
![]()
Множина яка не має жодного елемента називається порожньою:
Множина
А
називається підмножиною
множини В
тоді
і лише тоді, коли будь – який елемент
множини А
належить
множині В:
![]() .
Множина А,
що строго включена до В,
позначається так:
.
Множина А,
що строго включена до В,
позначається так:
![]() ,
це означає, що множина В
містить і інші елементи крім елементів
множини А.
,
це означає, що множина В
містить і інші елементи крім елементів
множини А.
Будь – яка множина є підмножиною самої себе. Порожня множина є підмножиною будь – якої множини. Тому у будь – якої множини є дві очевидних підмножини: порожня і сама ця множина.
Приклад:
![]() .
Підмножини множини А:
.
Підмножини множини А:
![]() .
.
Множина всіх підмножин множини А називається булеаном множини А і позначається: В (А) .
Теорема: кожна множина А, яка містить п елементів, має 2п підмножин.
![]()
![]()
![]()
Теорема: порожня множина є підмножиною будь – якої множини.
Нехай
дано дві множини: А
і .
Доведемо, що
![]() .
.
Припустимо,
що твердження
![]() хибне, тоді в порожній множині існує
елемент який не є елементом множини А,
а це неможливо, бо порожня множина не
містить елементів. Значить умова
хибне, тоді в порожній множині існує
елемент який не є елементом множини А,
а це неможливо, бо порожня множина не
містить елементів. Значить умова
![]() не є хибною.
не є хибною.
Дві
множини А
і В
називаються рівними,
коли кожний елемент множини А
є
елементом множини В
і навпаки:
![]() ,
,
![]()
![]()
Властивості множин:
-
рефлективність:
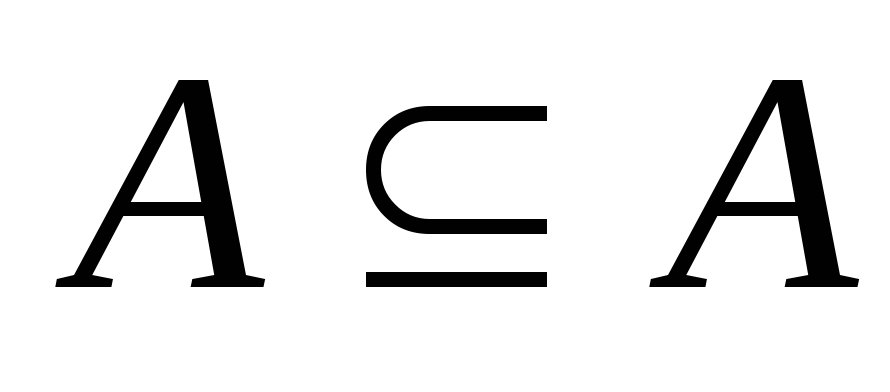 ;
; -
симетричність:
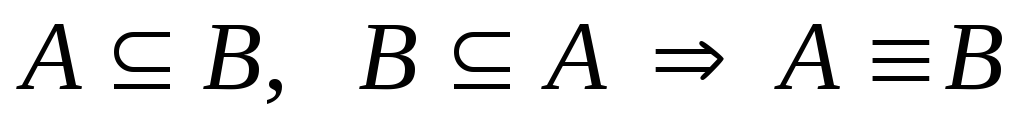 ;
; -
транзитивність:
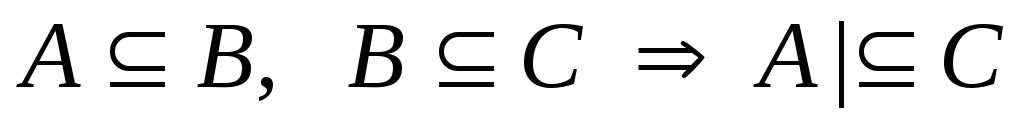
Способи задання множин:
Множина вважається заданою, якщо про будь – який об’єкт можна сказати чи належить він до даної множини чи ні.
-
Довільну скінченну множину можна задати переліком усіх її елементів.
Наприклад:
-
множину студентів групи можна задати їх списком у журналі;
-
С={червень, липень, серпень} – множина літніх місяців.
Спосіб задання множини переліком її елементів доцільно використовувати коли ця кількість не дуже велика. Так, множину всіх натуральних чисел, які менші 100000, можна задати переліком її елементів, але це займе дуже багато часу. У таких випадках використовують слідуючий запис: В={1; 2; 3; … ; 99998; 99999}. Знак … можна використовувати тоді, коли зрозуміло, які елементи вони замінюють.
-
Задання множин за допомогою характеристичної властивості.
Нескінченні множини неможливо задати переліком елементів, тому їх задають за допомогою характеристичної властивості
Означення. Ознака або властивість, якою володіють усі елементи даної множини і не володіють елементи, що не належать до даної множини, називається характеристичною властивістю для даної множини.
Характеристична властивість повинна бути такою, щоб було зрозуміло, чи належить даний об’єкт до множини, що розглядається.
Для
множин, які задаються характеристичною
властивістю їх елементів, використовують
запис:
![]() ,
де
,
де
![]() - скорочене позначення речення «елемент
х
має властивість Р
»
- скорочене позначення речення «елемент
х
має властивість Р
»
Приклади:
-
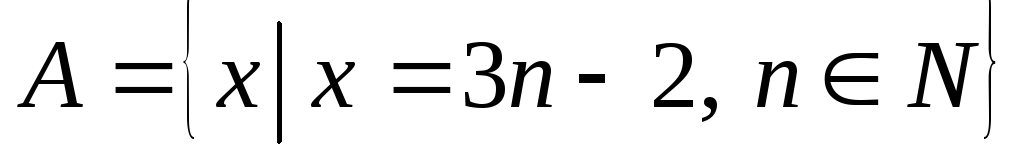 -
множина натуральних чисел, що при
діленні на 3
дають остачу 1.
-
множина натуральних чисел, що при
діленні на 3
дають остачу 1. -
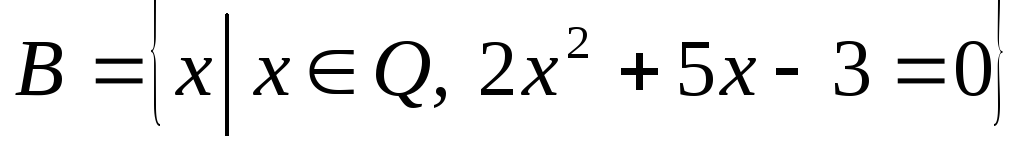 -
множина всіх раціональних коренів
рівняння.
-
множина всіх раціональних коренів
рівняння. -
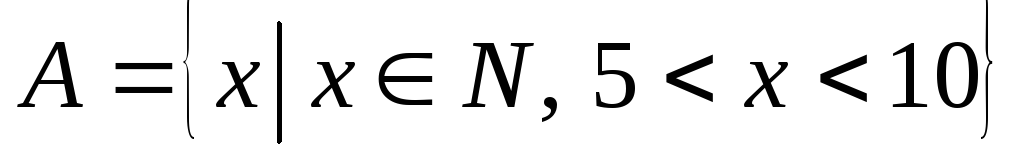 -
множина натуральних чисел між числами
5 і 10.
-
множина натуральних чисел між числами
5 і 10.
