7.2.2. Схема расположения полей допусков посадки ø40

На рисунок 24 показана схема полей допусков посадки Ø40

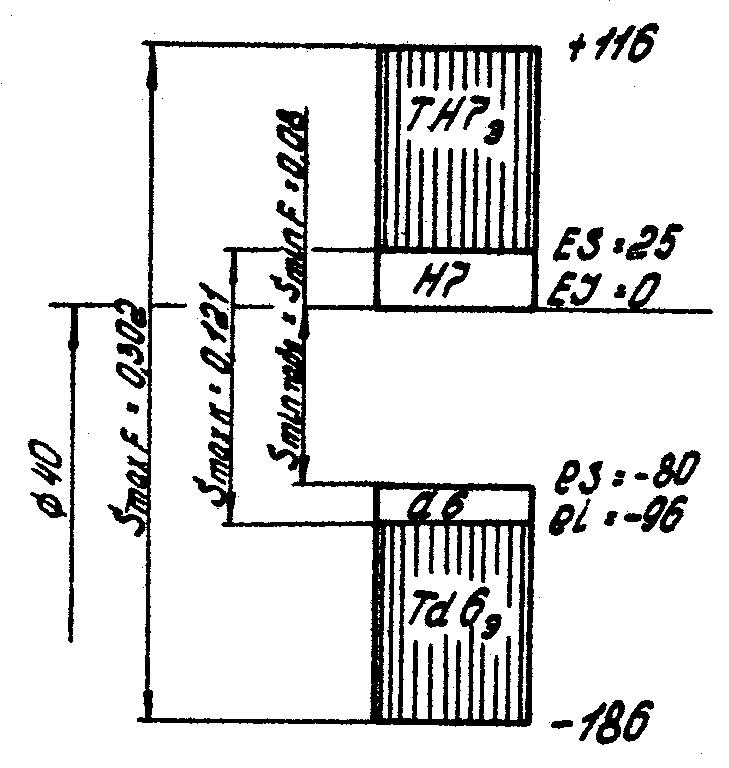
Рисунок 24. Схема расположения полей допусков посадки Ø40

для которой будут иметь место следующие размеры:

отверстия – ØH7_max = 40,025; ØH7_min = 40,0; TH7 = 0,025 мм; TH7э = 0,091 мм

вала – Ød6_max = 39,98; Ød6_min = 0,302; Td6 = 0,016 мм; Td6э = 0,121 мм

соединения – S_{min F} = 0,08; S_{max F} = 0,302; S_{min k} = 0,121; TS_K = 0,041; TS_Э = 0,181 мм

7. 3.Сопряжение 3- втулка 5 со стаканом 6

Данное сопряжение должно быть неподвижным, так как втулка 5, являясь подшипником скольжения, не должна проворачиваться в стакане 6. Такое соединение может быть достигнуто гарантированным натягом.

7.3.1. Расчет и выбор посадки с натягом для сопряжения 3

Чтобы обеспечить несдвигаемость втулки 5 относительно стакана 6, необходимо чтобы

где – момент трения шипа вала по поверхности d;

– момент трения наружной поверхности втулки по поверхности D.

Значения моментов трения определяются по известным [6] зависимостям

где R – радиальная нагрузка, действующая на цапфу вала, Н;

f₁, f – коэффициенты трения в соответствующих сопряжениях;

d₁, D – номинальные диаметры соответствующих сопряжений, М;

l – длина контакта сопрягаемых поверхностей, м;

p – удельное давление на контактных поверхностях, Н/м².

Отношение моментов трения определяет коэффициент запаса,

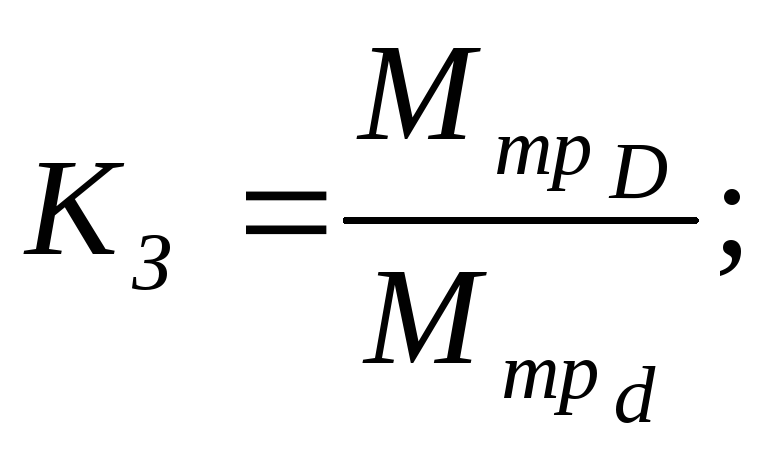
который выбирается в пределах 3...6. Подставляя в это уравнение значение моментов трения, находят удельное давление

Дальнейшее решение задачи аналогично решению задачи для сопряжения I, поэтому здесь не приводится. Расчётом установлено, что для сопряжения 3 должна быть выбрана посадка Ø50, которая соответствует заданным условиям.

7.4. Сопряжение 4 — стакан 6 с корпусом редуктора 8

Данное сопряжение является неподвижным, разъемным. Неподвижность его достигается с помощью болтов, следовательно, целесообразно использовать переходную посадку, а поскольку стаканы должны быть точно сцентрированы относительно друг друга, то вид сопряжения обеспечивает посадка Ø65.

7.4.1. Схема расположения полей допусков посадки ø65

На рисунок 25 приведена схема расположения полей допусков посадки Ø65,

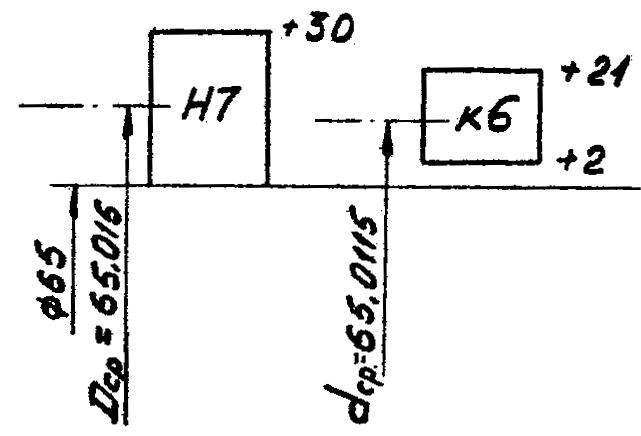
Рисунок 25. Схема расположения полей допусков посадки Ø65

для которой будут иметь место размеры:

отверстия – ØH7_max = 65,030; ØH7_min = 65,0; TH7 = 0,030 мм;

вала – Øk6_max = 65,021; Øk6_min = 65,002; Tk6 = 0,019 мм;

соединения – N_max = 0,021; S_min = 0,028; Т_{ПОСАДКИ} =0,049 мм.

7.4.2. Определение вероятности получения зазоров и натягов в посадке ø65

В предложении, что погрешности изготовления сопрягаемых деталей случайны и подчиняются закону нормального распределения, а центр их группирования совпадает с серединой поля допуска, определяется среднеквадратичное отклонение размеров сопрягаемых деталей по зависимости (37) — σ_D = 5, σ_d = 3,16

Поскольку средний размер отверстия больше среднего размера вала, то наиболее вероятным является соединение со средним зазором:

S_ср = 65,015 - 65,0115 = 0,0035 мм,

величина которого определяет положение центра группирования соединений с зазором относительно начала их отсчета (рисунок 26). На рисунке эта точка показана на оси Х'-Х' и соответствует значению 3,5 мкм.

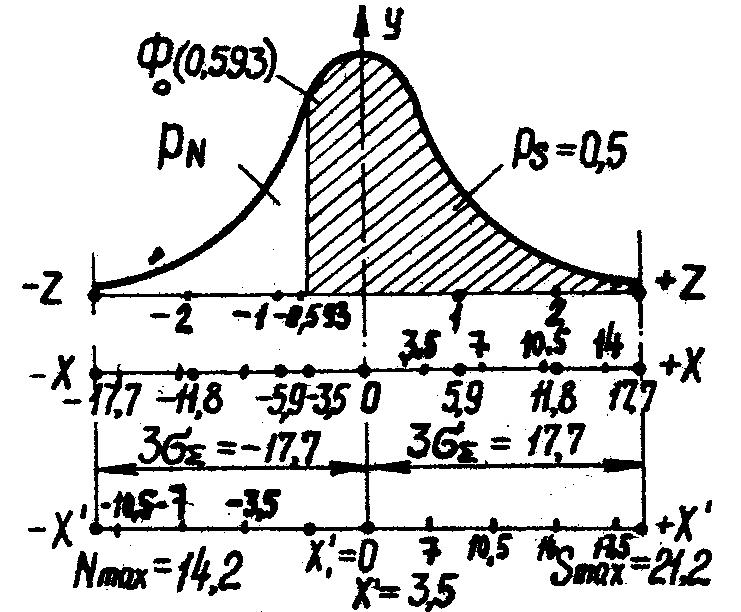
Рисунок 26. К определению вероятности получения зазоров и натягов в посадке

Среднее квадратическое отклонение размеров каждой из деталей в соответствии с (37):

Тогда среднее квадратическое суммарное отклонение определяется по зависимости (30):

Точка явяется координатой, отделяющей зазоры от натягов (на оси Х-Х она соответствует X =-3,5; на оси Z-Z −). Для большей наглядности на рисунке 26 показана ось Х-Х, на которой нанесены отклонения X = X′ − S_ср относительно X = 0, а относительно осей Z и У, где − вычерчена кривая нормального распределения. Заштрихованная площадь соответствует относительному количеству соединений с зазором, тогда относительное количество соединений с натягом определяется по зависимости (38):

В% = 100 - [Ф(0,593) + 0,5] · 100 = 27,76 %.

Значение Ф₀ (0,593) = 0,2224. Ее значение, как и плотность вероятности φ(z) взяты из приложений I и II [3]. Величины

а их зйачения отмечены на оси Х'-Х' рисунке26.