14. Коэффициент регрессии и выборочный коэффициент корреляции. Его свойства.

После этапа параметризации линейной парной регрессии было получено

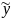= b0+b1x (1)

Параметр b1 наз–ся выборочным коэф-ом регрессии. Он показывает на сколько в среднем изм–ся перем–я y, если перем–я x ↑ на 1 ед–цу своего измерения.

В этом экономический смысл параметра b1. Параметр b0 не имеет спец. названия, как и в общемм случае экономического смысла.

Чисто формально b0 представляет знач–е перем y при x=0 и если перем–я x не может принимать нулевое знач–е, то и b0 не имеет эконом смысла. Из эконом смысла b1 следует, что он явл–ся измерителем тесноты связи y и x. Однако b1 зависит от единиц измер–я y и x. Наприер, если x измерять не в тоннах, а в кг, то параметр b1 ↓ в 1000 раз. Поэтому как хар–ка тесноты связи параметр b1 не удобен. Для получения хар–ки, не зависящей от размер–ти y и x, в кач–ве единиц измер–я берут среднее квадратич–ое отклонение перем–х y и x.

Для этого введем в рассмотрение :

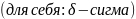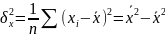
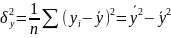
Вместо b0 в уравнении (1) запишем b0 =

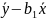
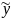= b0+b1x= - b1 + b1x= + b1( )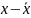

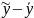= b1( )

↓ ↓ ↓

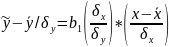
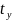
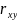
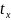
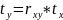(2)

это уравнение парной регрессии в стандартизированном виде, где ty и tx уже не имеет размерности.

= b1*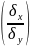 (3)

Коэф–т наз–ся выборочным коэф–ом парной корреляции. Он показывает на сколько в сред–м своих квадратич–х отклонений 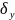изменится y, когда х ↑ на одно свое CКО .

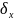Св–ва :

1. –1≤ rxy≤1

чем ближе │rxy│к 1, тем теснее связь м/у х и y.

Если >0, то связь прямая, <0, то связь обратная.

Если =1 или =–1. то м/у х и y сущ–ет линейная функциональная связь.

ГРАФИК

Если =0, то м/у х и y нет никакой связи и в этом случае y˜=y¯

ГРАФИК

Для промежуточных значений сущ–ет след шкала Чеддока по хар–ке связи.

Хар–ка связи: слабая умеренная заметная высокая весьма высокая

: 0,1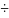 0,3 0,3 0,5 0,5 0,7 0,7 0,9 0,9 0,99

Другой важной хар–ой силы связи фактора х с результатом у явл–ся коэф–т эластичности. Различают средние и точечные (обобщенные и частные) коэф эластичности. Если перем-е х и у связывают урав–е у˜=f(х), тогда сред коэф эластичности подсчит–ся по формуле Э¯=(df/dx)*(x¯/f(x¯))

В частном случае для модели (1)

Э¯=b1*(x¯/y¯)

Частный коэф–т эластичности некоторой точки х0 вычисл–ся по формуле:

Э0=(df/dx)*(x0/f(x0))

Средний коэф–т эласт–ти показывает на сколько в среднем % изм–ся перем–я у, если перем–я х увелич–ся на 1% от своего сред–го знач–я.

Коэф–т эластичности – безразмерная величина (нет единицы измерения), м.б. и отрицательной.

15. Оценка точности уравнения парной линейной регрессии в целом

В основе проверки значимости ур–я регрессии и его точности наход–ся аппарат дисперсионного анализа.

Центральное место в дисперсионном анализе занимает положение о том, что для линейных моделей об–я сумма квадратов отклонения перем–ой у от своего сред знач–я у¯ пред–ся в виде 2–х частей:

Одна из них вызвана влиянием изуч–го фактора х, а др прочими неучтенными факторами, т. е.

Q=Σ(yi-y¯)² =Σ(yi˜-y¯)² + Σ(yi-yi˜)² (1)

Q = Q_R + Qe

Q_R– наз–т факторной суммой квадрата и она пред–т объясненную часть измененмя у.

Qe– наз–ют остаточной суммой квадрата, это не объясненная часть.

Если Q_R >Qe, то модель явл–ся статистич значимой, т.е. фактор х сущ–но вляет на у.

Если Q_R ≤Qe, то перем–я х не сущ–но влияет на у и ур–е регрессии не явл–ся статистич значимым.

В связи с этим вводят в рассм–е 1 из эффективных … адекватности линейной регрессионной модели– коэф детерминации.

R²= Q_R/Q = 1-(Qe/Q)= 1 – (Σ(yi-yi˜)²/Σ(yi-y¯)²) (2)

R² показывает какая часть (доля) вариации зависимой перем–ой у обусловлена изм–ем перем–ой х из формулы (2) след–т, что 0≤R²≤1

и чем ближе R к 1, тем лучше данная модель опраксимирует статистич данные. Например, R² = 0,87 (87% изменения у обусловлена изм-ем х, а на все остальные факторы 13%)

Для линейной парной регрессии справедлива след формула: R²=rxy²

Кроме равенства (1) сущ–ет равенство м/у числами степеней свободы об–ей, факторной и остаточной суммы квадратов.

n-1=1+(n-2)

Поделив факторную и остаточную сумму квадрата на соот–е число степене свободы, получим несмещенные оценки соот–х дисперсий.

S_R²=(Σ(yi˜-y¯)²) / 1 S²=(Σ(yi-yi˜)²) / (n-2)

Далее выдвигается гипотеза H₀: S_R²= S² (модель статистич не значима) для проверки гипотезы F= S_R²/ S²=((Σ(yi˜-y¯)²)*(n-2)) / ( Σ(yi-yi˜)²) (3)

которое имеет F–распред Фишера с числами степеней свободы k1=1, k2=n-2.

По формуле (3) подсчит–ют F_наб, а по таблице распред–я Фишера по заданной значимости α число степеней k1, k2 находится F_кр. Если F набл> F кр, то гипотеза H₀ отвергается и ур–е признается стастич значимым, а в противном случае – наоборот.

М/у коэф детерминации и F сущ–ет след связь: F=(R² / (1-R²))*(n-2)