50. Применение фиктивных переменных при моделировании сезонных колебаний ряда.

Если в структуре временного ряда(ВР) имеются циклич.колебания, то выравнивание ряда недопустимо, предварительно эти колебания надо исключить из исходных уровней ряда. Рассмотрим это на примере сезонных колебаний ВР.

Один из подходов заключ-ся в расчете значений сезонной компоненты и в построении либо аддитивной y_t =U_t+V_t+E_t модели ряда, либо мультипликативной модели ряда y_t =U_t*V_t*E_{t .}

Аддитивная модель выбирается в тех случаях, когда амплитуда сезонных колебаний с изменением времени не изменяется.

y_t =U_t+V_t+E_t

Мультипликат.модель выбир-ся, когда амплитуда сезонных колебаний со временем изм-ся.( напр, когда увеличивается)

y_t =U_t*V_t*E_t

Построение обеих моделей сводится к расчету знач. U_t,V_t,E_t для каждого уровня ряда. Сезонная компонента V_t должна удовлетворять след.условиям:

1)для аддитивной модели: сумма всех сезонных компонент за год должна равняться 0.

2)в случае мультипликат.модели произвед-е всех сезонных компонент за один цикл должны равняться 1.

В итоге, процесс построения модели включает в себя след.шаги.(для аддитивной модели). y_t =U_t+V_t+E_{t .}

1. выравнивание исходных уровней ряда методом скользящей средней. В итоге получается выравненный ряд, не содержащий сезонные компоненты.

2. расчет значений сезонной компоненты как разность м/у фактич-ми уровнями ряда и скользящими средними, полученными на первом шаге. Если полученные оценки сезонной компоненты не удовлетворяют приведенным требованиям, то они корректируются, чтобы эти требования выполнялись.

3. устранение сезонных компоненты из исходных уровней ряда y_t -V_t =U_t+E_{t .}

4. аналитическое выравнивание уровней ряда U_t+E_t.

5. по полученной модели тренда, расчёт +v_t и оценка точности модели.

Рассмотрим ещё один метод моделирования временного ряда, содержащего сезонные колебания. В этом методе наряду с независимой переменной t включаются фиктивные переменные, число кот-ых на единицу меньше числа периодов времени внутри одного цикла колебания.

Например, при моделировании поквартальных данных помимо перемен. t, исп-ют ещё 3 фиктивн.перемен. например, линейная модель тренда будет иметь вид: .

z_i =

i=

для 1,2,3-го квартала уравнение будет ,

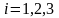
Для 4-го кварт.

В итоге, фиктивные переменные позволяют дифференцировать величину свободного члена уравн.регрессии для кажд.кварт.

Недостаток такого подхода заключается в большом кол-ве переменных модели.

Например, при описании данных для каждого месяца придется ввести в рассмотрение 11 фиктивных переменных и модель становится неудобной для фактического исп-я.

51. Тесты Чоу и Гуйарата для обнаружения структурных изменений ряда

От сезонных и циклических колебаний следует отличать единовременное изменение хар-ра тенденций временного ряда(ВР), вызванное структурными изм-ми в эк-ке или др.факторами.

В этих случаях, начиная с момента t* происходит изм-е хар-ра динамики изучаемого показателя, что приводит к изм-ю параметров тренда, описывающего эту динамику. В этом случае, одной из задач анализа ВР явл-ся выяснение вопроса: значимо ли повлияли общие структурные изм-я на хар-р тенденции ряда?

Если структурные изменения значимо повлияли, то для моделирование тенденции данного ряда следует исп-ть кусочно-линейные регрессии, т.е. исходную совок-ть данных разделить на две совокупности (до t* и после t*), для кажд. из кот-ых построить своё уравнение регрессии. Если же структурные изм-я не повлияли на тенденцию ряда, то его описывают единым по всей совокупности уровнем тренда. Для проверки структурной стабильности ряда используют ряд тестов, в частности в тесте Чоу Г. выдвигается нулевая гипотеза о незначительном структурн. изменении.

Согласно этому тесту гипотеза Н_о отвергается на уровне значимости α (т.е.признается наличие кусочно-линейного тренда, если статистика

>F_кр

превосходит F_кр , где F_кр определяется по таблице F_кр (α, k₁=p₁+p₂-p₃-1; k₂=n-p₁-p₂-2) n=n₁+n₂

n₁- число наблюдений до t*

n₂=n-n₁ - число набл.после t*

p₁,p₂-число параметров модели, построенных по данным до t* и по данным после t*, а p₃-по всей совокупности данных.

Таким образом, по критерию Чоу треб-ся построить 3 регрессионные модели:

1. по всей выборке ( )

2. по выборке объема n₁

3. по выборке объема n₂

Это считается недостатком теста Чоу.

Другой метод для обнаружения структурной стабильности предложил Гуйарати. Он предложил в уравнении регрессии включить фиктивн-ю переменную z_t, т.е. =b₀+b₁z_t+b₂t+b₃z_t*t

z_t=

тест Гуйарати сводится к оценке статистич .значимости параметров данного уравнения и использованием t-статистики. Могут быть 4 случая:

1. параметр b₁ явл-ся статистически значимым, а параметр b₃-нет. В этом случае изменение тенденции ряда вызвана различием свободных членов кусочно-линейной модели.

2. b₃ явл-ся статистически значимым, а b₁-нет. В этом случае кусочно-линейн.регрессии различ.коэф.регрессии.

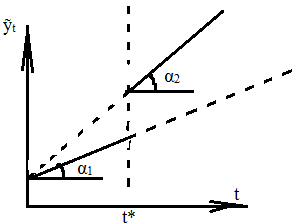
tgα₁=b₂+b₃

tgα₂=b₂

3. b₁ и b₃ – статистически значимы. В этом случае кусочно-линейные регрессии отличаются как коэф-ми регрессии, так и свободным членом.

4. b1 и b3 не явл-ся стат.значимым ,то используется единая по всей совокупности данных регрессия.

Преимущество теста Гуйарати над тестом Чоу заключ-ся в том, что треб-ся построить только одно уравнение регрессии.