
- •Случайные события. Вероятность. Теоремы сложения и умножения.
- •Случайные величины. Законы распределения дискретных и непрерывных случайных величин
- •Числовые характеристики дискретных и непрерывных случайных величин
- •Системы случайных величин. Законы распределения и числовые характеристики
- •Генеральная и выборочная совокупность. Выборочные характеристики
- •6. Основные распределения случайных величин, используемые в эконометрике.
- •7. Точечные оценки параметров распределений и требования к ним.
- •8.Интервальные оценки параметров распределений.
- •9. Общая схема статистической проверки гипотез.
- •10. Эконометрика как научная дисциплина. Общее понятие эконометрической модели.
- •11. Парный регрессионный анализ. Спецификация модели. Линейная парная регрессия
- •12. Предпосылки метода наименьших квадратов (мнк)
- •13. Мнк и мнк-оценки параметров парной регрессии. Теорем Гаусса-Маркова
- •14. Коэффициент регрессии и выборочный коэффициент корреляции. Его свойства.
- •15. Оценка точности уравнения парной линейной регрессии в целом
- •16. Оценка статистической значимости параметров линейной регрессии
- •17. Интервальные оценки для коэффициентов парной регрессии
- •18. Доверительная область для линии регрессии.
- •19. Доверительный интервал для прогнозных индивидуальных значений зависимой переменной
- •20. Коэффициент детерминации и средняя ошибка аппроксимации
- •21. Нелинейная парная регрессия. 2 типа нелинейных регрессий.
- •22. Линеаризация нелинейных моделей. Примеры.
- •23. Индексы корреляции и детерминации в нелинейных регрессиях.
- •24. Классическая нормальная линейная модель множественной регрессии.
- •26. Уравнение регрессии в стандартизованном масштабе
- •27. Честные коэффициенты корреляции
- •28. Коэффициенты множественной детерминации и корреляции
- •29. Оценка значимости уравнения в целом и его параметров в отдельности
- •30. Доверительный интервал для коэффициентов множественной регрессии
- •31. Доверительные интервалы для индивидуальных прогнозных значений зависимой переменной
- •32. Частные f-критерии и их использование в эконометрике
- •33. Мультиколлинеарность, ее разновидности, последствия и способы выявления
- •34. Методы устранения мультиколлинеарности
- •35. Гетероскедастичность и ее последствия
- •36. Методы обнаружения гетероскедастичности
- •37. Устранение гетероскедастичности. Взвешенный метод наименьшего квадрата.
- •38. Обобщенная модель множественной регрессии.
- •39. Автокорреляция, ее виды и последствия.
- •40. Методы обнаружения автокорреляции.
- •41.Оценка параметров при наличии автокорреляции.
- •42. Фиктивные переменные в регрессионных моделях.
- •43. Основные типы дискретных зависимых переменных.
- •44. Модели бинарного выбора. Линейная модель вероятности.
- •45. Probit-и logit- модели бинарного выбора. Модели множественного выбора.
- •46. Нелинейная множественная регрессия
- •47. Общие понятия временного ряда. Его составляющие. Типы моделей
- •48. Стационарные временные ряды. Коэффициент автокорреляции. Коррелограмма
- •49. Аналитическое и механическое выравнивание временного ряда
- •50. Применение фиктивных переменных при моделировании сезонных колебаний ряда.
- •51. Тесты Чоу и Гуйарата для обнаружения структурных изменений ряда
- •52.Нестационарные временные ряды.
- •53. Динамические модели. Модели авторегрессии и скользящей средней.
- •54. Модели с распределенным лагом и их характеристики
- •55. Модели Алмон и Койка.
- •56 Модель адаптивных ожиданий.
- •57. Общие сведения о системе одновременных уравнений (соу). Структурная и приведенная форма модели.
- •58. Косвенный мнк для соу.
- •59. Проблемы идентифицируемости соу. Необходимые ,достаточные условия идентифицируемости.
- •60. Двухшаговый метод наименьших квадратов.
- •61. Трехшаговый метод наименьших квадратов.
Числовые характеристики дискретных и непрерывных случайных величин
На ряду с законами распределения для описания СВ испол-ют числа, называемые числовыми характеристиками СВ. Различают числовые харак-ки положения СВ (мат. ожидание, мода, медиана и т.д.) и числовые харак-ки рассеивания (дисперсия, среднее квадрат отклонение, центральные моменты и т д)
Мат ожидание СВ характ-ет среднее ожидаемое значение СВ и определ-ся по формуле:

Мат ожидание обладает след. основными свойствами:
1.М(С)=С
2.М(СХ)=СМ(Х)
3.М(Х
 Y)=М(х)
M(Y)
Y)=М(х)
M(Y)
4. Если Х и Y–независимые величины, то M(XY) = M(X) * M(Y)
Дисперсия СВ D(X) определяется как матем. ожидание квадратов отклонения СВ от своего мат ожидания

Свойства дисперсии:
1.D(C)=0
2.D(CX)=C² D(X)
3.D(X Y)=D(X) + D(Y), если Х,У - независимые
СКО
вычисляется как δ(х)= =δ
=δ
Чтобы оценить разброс в % вводят коэфиц. вариации, определяемый по след. формуле:
V(x) = (δ(x) / lM(X)l ) *100%
Системы случайных величин. Законы распределения и числовые характеристики
Упорядоченный набор Х=(Х1,Х2,…,Хn) СВ Xi-ых i = 1,n называют системой СВ n-мерным случайным вектором.
Компоненты Xi м.б. как дискретными, так и непрерывными СВ. Они также м.б. как зависимыми, так и независимыми. Для описания случайного вектора используют след. понятия:
1) Совместную вероятность для ДСВ
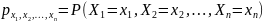
2)совместную функцию распределения как для ДСВ, так и для НСВ
F( )=P(
)=P( )
)
3)совместную плотность распределения для НСВ
f(
)
=
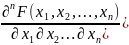
В частном случае, когда n=2, компоненты случайного вектора обозначают (X,Y) и вводят понятие условного закона распределения. Условным законом распределения в одной из равномерн. (одномерном) составляющ. Х или У назыв-ют и закон распределения. При условии, что другая составляющая приняла определенное численное значение.
Например,

Если
X,Y-независимые
СВ, то послед. Формула записывается:
Построение законов распределения случайных векторов представ. собой трудоемкий процесс. И поэтому для анализа связи СВ исп-ют 2 числовые характеристики:
-ковариацию
-коэффициент корреляции
Ковариацией (ковариац. Моментом) двух СВ X, Y назыв-ют математич. ожидание произведения отклонений этих СВ от своих мат ожиданий, т.е.
 =соv(X,Y)=M
((X
– mх)(Y-
mу)
= M(XY)
– mх*mу
=соv(X,Y)=M
((X
– mх)(Y-
mу)
= M(XY)
– mх*mу
Ковариация облад-ет след свойствами:
1.δху=δух
2.δхх=δ²х (дисперсия)
3.если Х,У- независ., то δху=0
4.соv(a + bX, с + dY) = bd cov (X,У)
Ковариации одновременно характер-ет взаимную зависимость Х, У и их рассеивание относительно своих мат. ожиданий. Это создает неудобство при интерпретации этой характеристики, в частности, эта характ-ка имеет другой недост-ок: она зависит от размерности Х,У. Этого недостатка лишен коэффициент корреляции, определяемый по формуле:

В итоге, коэфиц. корреляции уже не зависит от размерности Х,У и характеризует только степень зависимости Х,У.
Св-ва коэф. корреляции:

 =
1
=
1-1 ≤
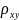 ≤ 1
≤ 1если Х,У-незав., то
 .
Обратное не верно
.
Обратное не верноЕсли | | = 1, то Х = а + bY
Общая
формула:
 ,
если Х,У – зависимые.
,
если Х,У – зависимые.
Для случая, когда случ. вектор явл-ся n-мерным рассм-ют ковариационную матрицу, являющуюся аналогом дисперсии одномерной СВ


Степень зависимости составляющих случайного вектора характер-ет матрица парных коэф-ов корреляции. Корреляционная матрица:

