32. Частные f-критерии и их использование в эконометрике

Не каждый фактор, дополнительно включенный в модель, может существенно увеличить долю объясняемой вариации зависимой переменной. Ввиду корреляции м/у факторами, значимость влияния одного и того же фактора м.б. различной в зависимости от последовательности включения его в модель. Мерой оценки значимости улучшения качества модели, после включения в нее дополнительного фактора , служит частный критерий, который опред-ся по след. формуле:

Здесь: - коэффициент множ-ой детерминации без фактора в модели. – коэффициент множ-ой детерминации с фактором . По таблицам Распределения Фишера наход-ся по уровню значимости и числом степеней свободы .

Если , то включение в модель явл-ся оправданным, т.к. он существенно улучшает качество модели. В противном случае это включение нецелесообразно.

Если р = 2, то исп-ся 2 частных F-критерия:

(1)

По таблице распределения Фишера находим по и

Если , то включение фактора в модель после того, как в нее был включен фактор является целесообразным. Поскольку фактор существенно улучшает качество модели. В противном случае, т.е. если , то включение в модель после того, как в нее был включен фактор нецелесообразно. Параметр при не будет статистически значимым.

Пусть по п наблюдениям построено уравнение регрессии с р факторами. При этом, коэффициент детерминации = . Исключим из рассмотрения k объясняющих переменных, которые показались нам лишними. Получим новую модель Проверяем . Для проверки гипотезы исп-ся след. F-критерий:

. По таблице Фишера: по и .

Если , то отвергается, т.е. коэф множ-ой детерминации существенно различно и исключение факторов из модели недопустимо. Аналогично можно проверить обоснованность дополнительного включения в модель факторов. В этом случае исп-ют F-статистику:

33. Мультиколлинеарность, ее разновидности, последствия и способы выявления

Под мультиколлинеарностью понимают высокую взаимную коррелируемость объясняющих переменных (факторов). Мультиколлинеарность проявляется либо в функциональных, либо в стохастических формах. В 1-ом случае по крайней мере 1 пара из объясняющих переменных, связанный линейной функциональной зависимостью и в этом случае говорят о строгой мультиколлинеарности. В матрице Х в этом случае по крайней мере 2 столбца являются линейно зависимыми. И тем самым нарушается предпосылка 6 (в матрице Х столбцы д.б. независимыми, т.е. ранг матрицы должен = р +1) и . В этом случае матрица Х’Х будет вырожденной, т.е. . И система нормальных уравнений будет неразрешима, т.к. не существует. В итоге вектор b не определяется. Геометрически это можно проиллюстрировать след. образом:

Однако, строгая мультиколлинеарность встречается редко, т.к. ее не сложно избежать на стадии предварительного отбора факторов в модель. Чаще связь между объясняющими переменными выражена в стохастической форме, когда они тесно коррелируют друг с другом. В этом случае говорят о нестрогой мультиколлинеарности. Матрица 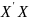хотя и не явл-ся вырожденной, но ее

, а поскольку оценка обратно пропорциональна определителю:

, где - присоединенная матрица к , то при делении на величину 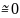получается большая неточность в определении компонентов вектора b. Дисперсии оценок получаются большими, их несмещенные оценки 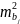также становятся большими. Они имеют большой разброс относительно . В этом случае они не устойчивы, не стабильны как по величине, так и по знаку. И становятся очень чувствительными к незначительному изменению исходных данных.

О тметим следующие основные негативные последствия в мультиколлинеарности:

1. Большие дисперсии оценок параметров приводят к большим отклонениям этих оценок от значения оцениваемых параметров. Увеличивают интервальные оценки, тем самым ухудшая их точность

2. Уменьшаются 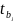(t-статистики) параметров, что приводит к неправильному выводу о статистической незначимости параметра и несущественном влиянии соответствующего фактора на результат у.

3. оценки становятся очень чувствительными к незначительному изменению исходных статистических данных.

4. Становится невозможным определить изолированное влияние отдельных факторов на результирующий показатель.

Точных количественных методов по обнаружению мультиколлинеарности не сущ-ет. Однако, есть несколько эвристических методов по ее выявлению.

1-ый из них связан с исследованием матрицы межфакторной корреляции:

Считается, что если в ней имеются коэф-ты межфакторной корреляции , то это говорит о наличии нестрогой мультиколлинеарности.

2-ой способ заключается в вычислении

Если , то мы имеем строгую мультиколлинеарность

Если , то нестрогая мультиколлинеарность

3-ий способ заключается в вычислении определителя матрицы межфакторной корреляции: .

Если

Если

мультиколлинеарность отсутствует. Для проверки гипотезы исп-ют след. статистику: , которая приблизительно имеет распределение с k = 1/2 (n-1)*n.

Вычисляют . И по таблице - распределение находят: по и k. Если , то Н₀ отвергают с вероятностью ( в пользу альтернативной, т.е. наличие нестрогой мультиколлинеарности.

4-ым способом выявления мультиколлинеарности является исследование коэф-ов множественной детерминации, показывающих зависимость фактора от других объясняющих переменных модели. Например, строят регрессионную модель:

. И на основании этой модели вычисляется - коэффициент множественной корреляции. В результате получаем . Снова проверка гипотез: т.е. фактор не зависит от всех остальных (мультиколлинеарности нет).

, (F-распределение).

По таблице . Если , то отвергается и (нестрогая мультиколлинеарность.