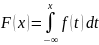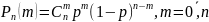- •Случайные события. Вероятность. Теоремы сложения и умножения.
- •Случайные величины. Законы распределения дискретных и непрерывных случайных величин
- •Числовые характеристики дискретных и непрерывных случайных величин
- •Системы случайных величин. Законы распределения и числовые характеристики
- •Генеральная и выборочная совокупность. Выборочные характеристики
- •6. Основные распределения случайных величин, используемые в эконометрике.
- •7. Точечные оценки параметров распределений и требования к ним.
- •8.Интервальные оценки параметров распределений.
- •9. Общая схема статистической проверки гипотез.
- •10. Эконометрика как научная дисциплина. Общее понятие эконометрической модели.
- •11. Парный регрессионный анализ. Спецификация модели. Линейная парная регрессия
- •12. Предпосылки метода наименьших квадратов (мнк)
- •13. Мнк и мнк-оценки параметров парной регрессии. Теорем Гаусса-Маркова
- •14. Коэффициент регрессии и выборочный коэффициент корреляции. Его свойства.
- •15. Оценка точности уравнения парной линейной регрессии в целом
- •16. Оценка статистической значимости параметров линейной регрессии
- •17. Интервальные оценки для коэффициентов парной регрессии
- •18. Доверительная область для линии регрессии.
- •19. Доверительный интервал для прогнозных индивидуальных значений зависимой переменной
- •20. Коэффициент детерминации и средняя ошибка аппроксимации
- •21. Нелинейная парная регрессия. 2 типа нелинейных регрессий.
- •22. Линеаризация нелинейных моделей. Примеры.
- •23. Индексы корреляции и детерминации в нелинейных регрессиях.
- •24. Классическая нормальная линейная модель множественной регрессии.
- •26. Уравнение регрессии в стандартизованном масштабе
- •27. Честные коэффициенты корреляции
- •28. Коэффициенты множественной детерминации и корреляции
- •29. Оценка значимости уравнения в целом и его параметров в отдельности
- •30. Доверительный интервал для коэффициентов множественной регрессии
- •31. Доверительные интервалы для индивидуальных прогнозных значений зависимой переменной
- •32. Частные f-критерии и их использование в эконометрике
- •33. Мультиколлинеарность, ее разновидности, последствия и способы выявления
- •34. Методы устранения мультиколлинеарности
- •35. Гетероскедастичность и ее последствия
- •36. Методы обнаружения гетероскедастичности
- •37. Устранение гетероскедастичности. Взвешенный метод наименьшего квадрата.
- •38. Обобщенная модель множественной регрессии.
- •39. Автокорреляция, ее виды и последствия.
- •40. Методы обнаружения автокорреляции.
- •41.Оценка параметров при наличии автокорреляции.
- •42. Фиктивные переменные в регрессионных моделях.
- •43. Основные типы дискретных зависимых переменных.
- •44. Модели бинарного выбора. Линейная модель вероятности.
- •45. Probit-и logit- модели бинарного выбора. Модели множественного выбора.
- •46. Нелинейная множественная регрессия
- •47. Общие понятия временного ряда. Его составляющие. Типы моделей
- •48. Стационарные временные ряды. Коэффициент автокорреляции. Коррелограмма
- •49. Аналитическое и механическое выравнивание временного ряда
- •50. Применение фиктивных переменных при моделировании сезонных колебаний ряда.
- •51. Тесты Чоу и Гуйарата для обнаружения структурных изменений ряда
- •52.Нестационарные временные ряды.
- •53. Динамические модели. Модели авторегрессии и скользящей средней.
- •54. Модели с распределенным лагом и их характеристики
- •55. Модели Алмон и Койка.
- •56 Модель адаптивных ожиданий.
- •57. Общие сведения о системе одновременных уравнений (соу). Структурная и приведенная форма модели.
- •58. Косвенный мнк для соу.
- •59. Проблемы идентифицируемости соу. Необходимые ,достаточные условия идентифицируемости.
- •60. Двухшаговый метод наименьших квадратов.
- •61. Трехшаговый метод наименьших квадратов.
Случайные события. Вероятность. Теоремы сложения и умножения.
Случайным событием называется любой факт, кот. при осуществлении совокупности условий может произойти либо не произойти (А, В, А1, А2).
События
назыв. несовместимыми,
если появление одного из них исключает
появление других в одном и том же
испытании. Два события А и
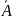 назыв.
противоположными,
если одно из них происходит тогда и
только тогда, когда не происходит другое.
назыв.
противоположными,
если одно из них происходит тогда и
только тогда, когда не происходит другое.
События, кот. нельзя разбить на более простые назыв. элементарными.
Вероятность события – это количественная мера, кот вводится для сравнения событий по степени возможности их проявления в испытании. В частности, классическое определение вероятности вычисляется как отношение числа m элементарных событий, благоприятствующих появлению некоторого события А к числу n всех элементарных событий в условиях данного эксперимента, т.е. Р(А)=m/n
Свойства вероятности:
1)0≤P(A)≤1
2)P(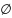 )
= 0 (невозмож. событие); P(Ω)=1
(достоверное событие)
)
= 0 (невозмож. событие); P(Ω)=1
(достоверное событие)
3)P(A)=1- P( )
Событие А и В наз-ся независимыми, если вероятность каждого из них не зависит от того произошло или нет другое событие. Вероятность события А, вычисленную в предположении, что другое событие В уже произошло назыв-ют условной вероятностью и обозначают: Р(А/В) или Рв(А)
Верна след. теорема умножения вероятностей: вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого. Т.е. Р(АВ)=Р(А)*Р(В/А)=Р(В)*Р(А/В)
В частности для независим. событий теорема умножения упрощается: Р(АВ)=Р(А)*Р(В)
Теорема сложения: Вероятность суммы 2-х событии равна сумме вероятностей этих событий - вероятность их произведения, т.е. Р(А+В)=Р(А)+Р(В) - Р(АВ)
В частном случае когда А и В несовместны формула упрощается: Р(А+В)=Р(А)+Р(В)
Случайные величины. Законы распределения дискретных и непрерывных случайных величин
Случайной величиной назыв. величину, кот. в результ испытания примет одно и только одно из своих возможных значений заранее не известное и зависящее от случайных причин (X, Y, Z).
Различают дискретные и непрерывные СВ (случайные величины). Дискретной назыв. такую СВ, кот принимает отдельные изолированные значения с определенными вероятностями.
Непрерывной назыв-ся СВ, кот может принимать любое значение из некоторого конечного или бесконечного чис-го промежутка.
Наиболее полным исчерпывающим описанием СВ является его закон распределения для Дискретной СВ (ДСВ) закон распределения можно задать в таблице, графически или формулой
В 1-ом случае:
х
х1
х2
…
хп
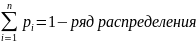
р
р1
р2
…
рп
Во 2-ом случае:
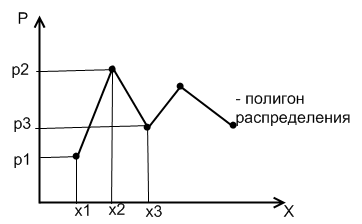
Для непрерывной СВ (НСВ) конкретное значение невозможно. Поэтому не Р(Х = х), а Р(Х < х). Функцией распределения вероятностей СВ наз-ся функция F(x), определяющая вероятноть того, что СВ примет значение < X, т.е. F(x) = Р(Х < х).
Свойства функции распределения:
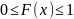
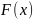 – неубывающая
функция
– неубывающая
функция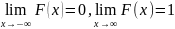
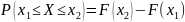
Графически функция распределения для ДСВ и НСВ:
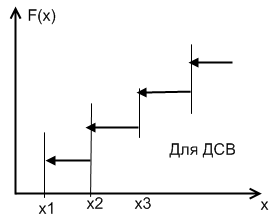
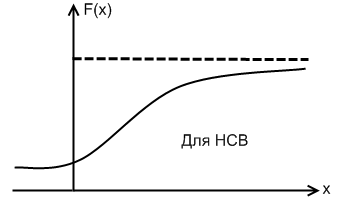
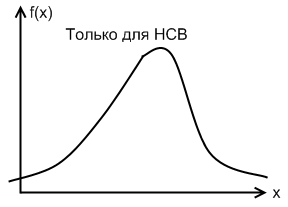
Для НСВ вводят в рассмотрение 2-ой закон распределения вероятностей -плотность распределения вероятностей f(x) = F’(x) = dF(x) / dx. А для ДСВ не сущ-ет, т.к. F’(x) = 0.
Свойства плотности распределения:
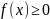 3)
3)
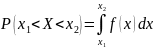
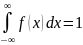 4)
4)