3.2. Напруження в кільці та сфері.
Задача 6. Дослідження пружних напружень в кільці. Розв’язок цієї задачі наведено в п. 2.1.
Спочатку
наведемо розраховані програмою розподіл
радіальних і кільцевих напружень для
двох випадків навантаження при
- рис.3.11.
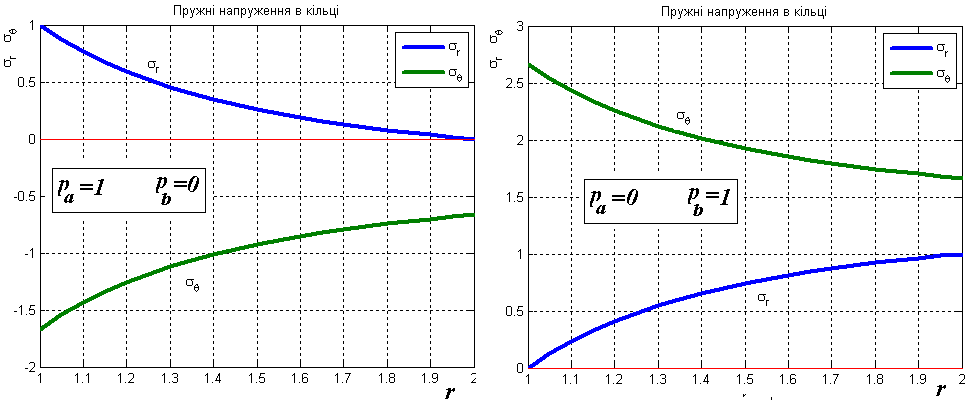
Рис.
3.11. Напруження в пружному кільці.
Зліва
;
справа
.
Для роботи програми необхідно задати (відкорегувати) дані на її початку.
Задамо дані:
a=1; b=2; pa=0; pb=1; nju=0.3;
% Розрахунок
h=(b-a)/20; r=a:h:b;
eps2=(a/b)^2;c=(1-nju)/(1+nju);
A=pb/(1-c*eps2);B=-c*A;
sr=B*a*a./r.^2+A; st=-B*a*a./r.^2+A;
figure
plot(r,sr,r,st,'linewi',3); grid on;hold on; plot(r,r*0,'r','linewi',1);
title('Пружні напруження в кільці');
legend('\sigma_r','\sigma_\theta');
xlabel('r'); ylabel(['\sigma_r',' ','\sigma_\theta']);
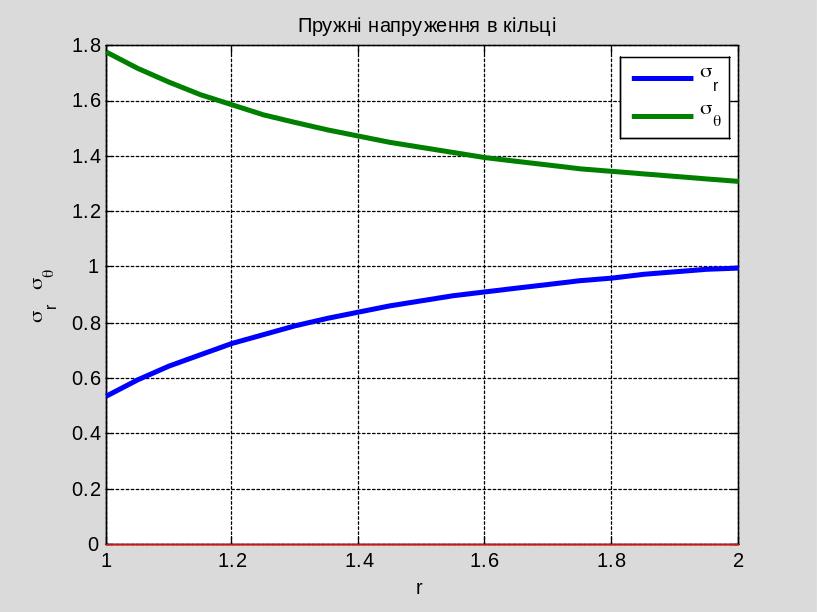
Розглянемо
загальний випадок, коли модуль Юнга та
коефіцієнт Пуассона є змінними величинами
і залежать від радіальної координати,
тобто
.
При
змінних величинах
систему рівнянь необхідно розв’язувати
числово. Позначимо
.
Тоді отримаємо систему рівнянь
(2.12)
Кільцеві напруження знаходяться так
Граничні умови.
Нехай
при
відомі
.
Тоді буде задана
.
Нехай
задано перміщення
.
Враховуючи, що
. Звідси
маємо умову
.
% cd('d:\Maxymovych\Nawchan\Методички 2010\'); systema_rivn_kiljce
nu=0.3; pa=0; pb=1;
a=1; b=3; n=20;
% Вигляд кільця
t=0:pi/60:2*pi;
xa=a*cos(t); ya=a*sin(t);
xb=b*cos(t); yb=b*sin(t);
figure; subplot(1,2,1)
fill(xb,yb,[1 1 1]*0.9); hold on; fill(xa,ya,[1 1 1]*0.98); hold on;
plot(xa,ya,'b',xb,yb,'b','linewi',3);
axis equal;title(['Кільце;' ' p_a=',num2str(pa), '; p_b=',num2str(pb)]); grid on
% Запис рівнянь і граничних умов
ab=(a+b)/2;
funE=@(x)(x+ab)/ab; funN=@(x)0.25*(x/ab);
rivn=@(x,y)[-(1-funN(x))./x.*y(1)+y(2)./x.^2.*funE(x);
(1-funN(x).^2)*y(1)./funE(x)-funN(x).*y(2)./x];
gran = @(ya,yb)[ya(1)-pa;
yb(1)-pb];
%Задання початкового наближення для функції St і U похідної
fun=@(x)[cos(x); sin(x)];
x=a+(b-a)/n*[0:n];
yinit=bvpinit(x,fun);
%---- РозвЯзування задачі ------------------------------
Y1=bvp4c(rivn,gran,yinit);
x1=a+(b-a)/50*[0:50];
y1=deval(Y1,x1);
st=funN(x1).*y1(1,:)+y1(2,:)./x1.*funE(x1);
subplot(1,2,2)
sr=y1(1,:); M=max([sr,st]);co=b/M*0.75;
plot(x1,sr*co,x1,st*co,'r','linewi',3) ;
xlabel('r'); ylabel(['\sigma_r',' ','\sigma_\theta']);
hold on
h=plot(xa,ya,'b',xb,yb,'b','linewi',2);axis equal
grid on; hold on
plot([x(1),x(1)],[sr(1),st(1)]*co,[x(end),x(end)],[sr(end),st(end)]*co,'linewi',2);
text(x(1)+a/4,sr(1)*co*1.,['\sigma_r=',num2str(sr(1),3)],'fontsize',12)
text(x(1)+a/4,st(1)*co*1.,['\sigma_\theta=',num2str(st(1),3)],'fontsize',12)
text(x(end),sr(end)*co-b/10,['\sigma_r=',num2str(sr(end),3)],'fontsize',12)
text(x(end),st(end)*co+b/10,['\sigma_\theta=',num2str(st(end),3)],'fontsize',12)
Температурна задача
Позначимо
,
–
довільне значення. Тоді система рівнянь
запишеться для змінного пружних
характеристик запишеться
Кільцеві напруження знаходяться за формулою
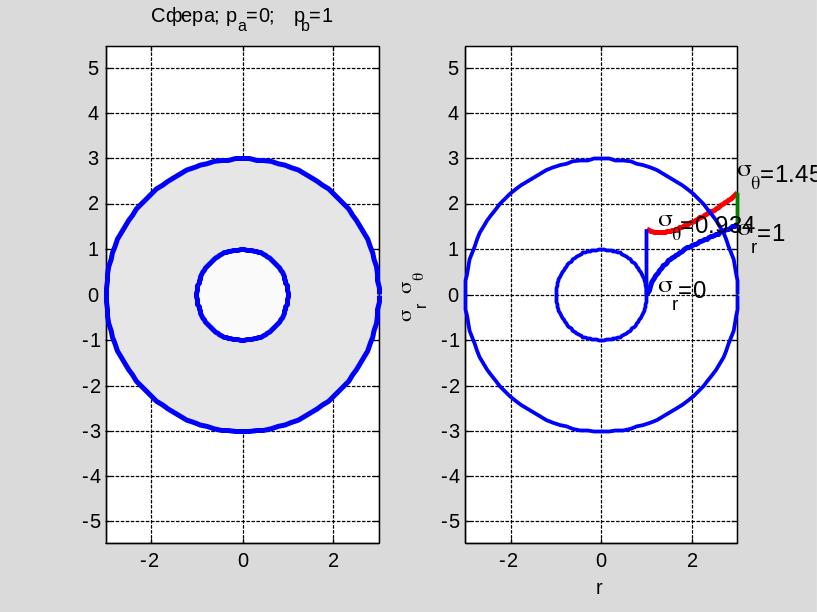
Задача 7. Розглянемо тіло, що має вигляд сфери з порожниною . Приймемо, що до внутрішньої та зовнішньої межі прикладено зусилля
Нехай при відомі . Тоді буде задана .
Нехай задано перміщення . Враховуючи, що
. Звідси
маємо умову
.
Позначимо . Тоді система рівнянь (2.18) запишеться у вигляді
де
.
Кільцеві напруження визначаються за формулою
.
nu=0.3; pa=0; pb=1;
a=1; b=3; n=20;
% Вигляд тіла
t=0:pi/60:2*pi;
xa=a*cos(t); ya=a*sin(t);
xb=b*cos(t); yb=b*sin(t);
figure; subplot(1,2,1)
fill(xb,yb,[1 1 1]*0.9); hold on; fill(xa,ya,[1 1 1]*0.98); hold on;
plot(xa,ya,'b',xb,yb,'b','linewi',3);
axis equal;title(['Сфера;' ' p_a=',num2str(pa), '; p_b=',num2str(pb)]); grid on
% Запис рівнянь і граничних умов
ab=(a+b)/2;
funE=@(x)(x+ab)/ab; funN=@(x)0.25*(x/ab);
a11=@(x)-2*(1-2*funN(x))./(1-funN(x))./x;
a12=@(x) 2*funE(x)./(1-funN(x))./x.^2;
a21=@(x)(1-funN(x)-2*funN(x).^2)./(1-funN(x))./funE(x);
a22=@(x)-2*funN(x)./(1-funN(x))./x;
rivn=@(x,y)[a11(x)*y(1)+a12(x)*y(2);
a21(x)*y(1)+a22(x)*y(2)];
gran = @(ya,yb)[ya(1)-pa;
yb(1)-pb];
%Задання початкового наближення для функції St і U похідної
fun=@(x)[cos(x); sin(x)];
x=a+(b-a)/n*[0:n];
yinit=bvpinit(x,fun);
%---- РозвЯзування задачі ------------------------------
Y1=bvp4c(rivn,gran,yinit);
x1=a+(b-a)/50*[0:50];
y1=deval(Y1,x1); %
st=(funN(x1).*y1(1,:)+y1(2,:).*funE(x1)./x1)./(1-funN(x1));
subplot(1,2,2)
sr=y1(1,:); M=max([sr,st]);co=b/M*0.75;
plot(x1,sr*co,x1,st*co,'r','linewi',3) ;
xlabel('r'); ylabel(['\sigma_r',' ','\sigma_\theta']);
hold on
h=plot(xa,ya,'b',xb,yb,'b','linewi',2);axis equal
grid on; hold on
plot([x(1),x(1)],[sr(1),st(1)]*co,[x(end),x(end)],[sr(end),st(end)]*co,'linewi',2);
text(x(1)+a/4,sr(1)*co*1.,['\sigma_r=',num2str(sr(1),3)],'fontsize',12)
text(x(1)+a/4,st(1)*co*1.,['\sigma_\theta=',num2str(st(1),3)],'fontsize',12)
text(x(end),sr(end)*co-b/10,['\sigma_r=',num2str(sr(end),3)],'fontsize',12)
text(x(end),st(end)*co+b/10,['\sigma_\theta=',num2str(st(end),3)],'fontsize',12)
