Розв’язання

Якщо 3x + 2y = 9, то 3x = –2y + 9 (правило перенесення доданків); (правило ділення).

а) Якщо y = 6, то x =   = –2 · 2 + 3 = –4 + 3 = –1. (–1; 6) — розв’язок рівняння.

б) Якщо y = –9, то x =   = –2 · (–3) + 3 = 6 + 3 = 9. (9; –9) — розв’язок рівняння.

2. Графіки лінійних рівнянь із двома змінними

Графіком лінійного рівняння з двома змінними, в якому хоча б один (один або обидва) з коефіцієнтів при змінних відмінний від нуля, є пряма.

Коротко, графіком будь-якого лінійного рівняння першого степеня є пряма.

Навпаки, кожна пряма координатної площини є графіком деякого лінійного рівняння з двома змінними.

Приклад.

Графіками лінійних рівнянь 5x + 0y = 7; 0x + 4y = 3; 4x + 5y = 2; 4x + 3y = 0 є прямі.

Графіком лінійного рівняння з двома змінними 0x + 0y = 0, в якому всі коефіцієнти при змінних і вільний член дорівнюють нулю, є вся координатна площина.

Коротко, рівнянням координатної площини є рівняння 0x + 0y = 0.

Лінійні рівняння, у яких обидва коефіцієнти дорівнюють нулю, а вільний член відмінний від нуля, тобто рівняння виду 0x + 0y = c, де c  0, не мають графіків.

Приклад.

Лінійні рівняння 0x + 0y = 4; 0x + 0y = –1; 0x + 0y = 0,1 не мають графіків.

Обґрунтування

Розв’язком рівняння 0x + 0y = 0 є будь-які пари чисел. Отже, будь-яка точка координатної площини є точкою графіка цього рівняння.

Рівняння виду 0x + 0y = c, де c  0, не мають розв’язків. Отже, на координатній площині немає точок, які були б точками цього графіка.

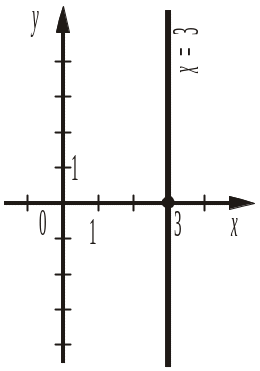
Графіком рівняння x = m на координатній площині є пряма, яка перетинає вісь x у точці з абсцисою m і перпендикулярна до цієї осі (тобто паралельна до осі y).

Обґрунтування

Рівняння x = m можна записати як x + 0y = m, розв’язком якого є усі пари чисел, у яких значення змінної x дорівнює m, а y — будь-яке число. Такі розв’язки зображають на координатній площині точками, у яких абсциса дорівнює m, а ордината — будь-яке число. Усі ці точки належать прямій, перпендикулярній до осі x і яка перетинає її у точці з абсцисою m.

Приклади.

Рис. 13	Рис. 14	Рис. 15	Рис. 16

Щоб побудувати пряму, яка є графіком рівняння першого степеня ax + 0y = c, потрібно:

• подати рівняння у вигляді рівняння першого степеня з однією змінною: ax = c;

• знайти абсцису точки перетину графіка з віссю x: ;

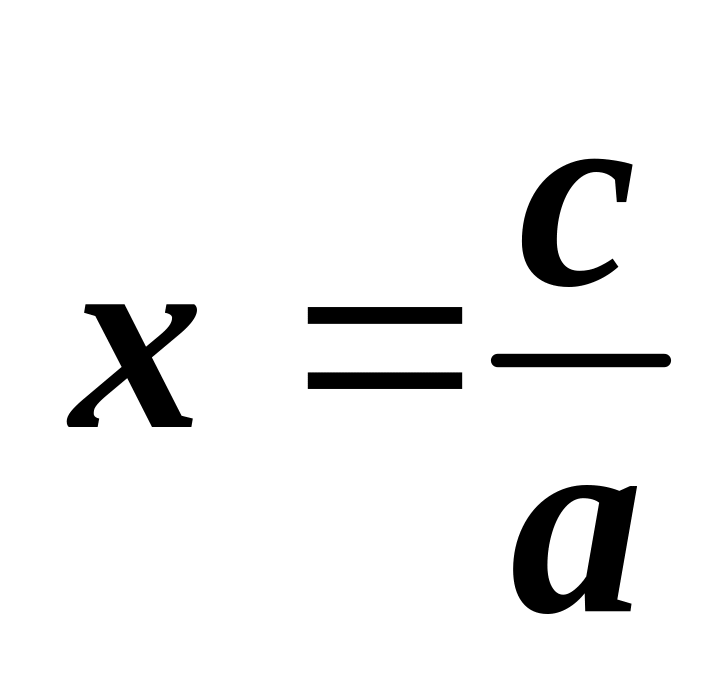• провести через точку 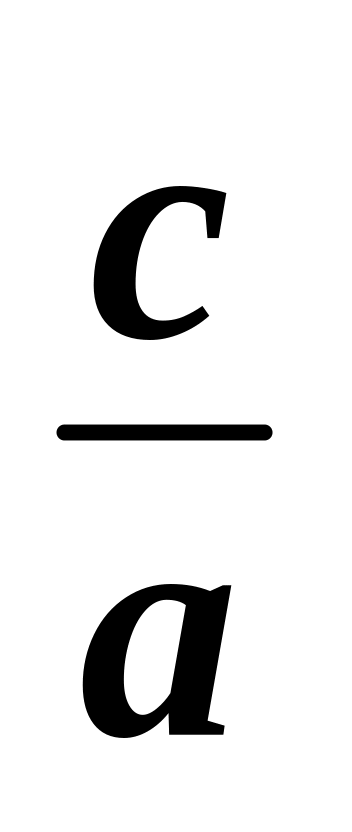осі x пряму, перпендикулярну до неї.

Проведена пряма і є графіком рівняння ax + 0y = c.

П риклад.

Побудувати графік рівняння 2x + 0y = 8.

1) Записуємо дане рівняння як рівняння першого степеня з однією змінною: 2x = 8.

2) Розв’язуємо його: x = 4.

3) Позначаємо на осі x точку з абсцисою 4 і проводимо через неї пряму, перпендикулярну до осі x (рис. 17).

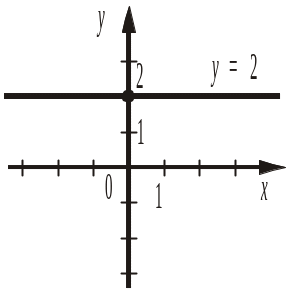
Графіком рівняння y = n на координатній площині є пряма, яка перетинає вісь y у точці з ординатою n і перпендикулярна до цієї осі (тобто паралельна до осі x).

Приклади.

Рис. 18	Рис. 19	Рис. 20	Рис. 21

Щоб побудувати пряму, яка є графіком рівняння першого степеня 0x + by = c, потрібно:

• подати рівняння у вигляді рівняння першого степеня з однією змінною: by = c;

• знайти ординату точки перетину графіка з віссю y: ;

• провести через точку 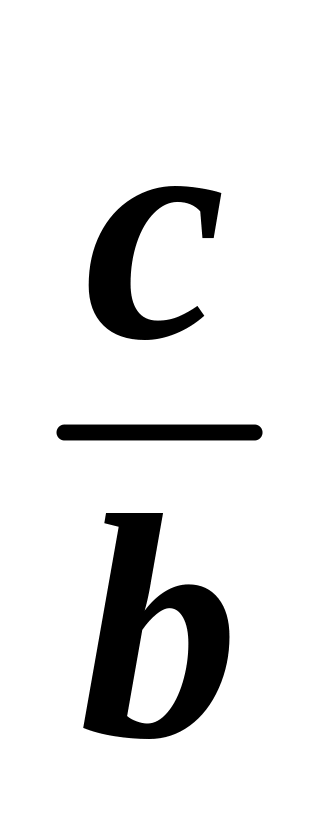осі y пряму, перпендикулярну до неї.

Проведена пряма і є графіком рівняння 0x + by = c.

П риклад.

Побудувати графік рівняння 0x + 2y = 6.

1) Записуємо дане рівняння як рівняння першого степеня з однією змінною: 2y = 6.

2) Розв’язуємо його: y = 3.

3) Позначаємо на осі y точку з ординатою 3 і проводимо через неї пряму, перпендикулярну до осі y (рис. 22).

Щоб побудувати пряму, яка є графіком рівняння першого степеня ax + by = c, потрібно:

• знайти два його розв’язки;

• зобразити розв’язки точками координатної площини;

• провести через ці точки пряму.

Проведена пряма і є графіком рівняння ax + by = c.

Приклади.

1. Побудувати графік рівняння x + y = 4.

1) Знаходимо два розв’язки. Нехай x = 0, тоді 0 + y = 4; y = 4; розв’язок (0; 4); нехай y = 0, тоді x + 0 = 4; x = 4; розв’язок (4; 0).

2) Будуємо на координатній площині точки А(0; 4) і В(4; 0).

3) Проводимо пряму АВ (рис. 23). Дана пряма є графіком рівняння x + y = 4.

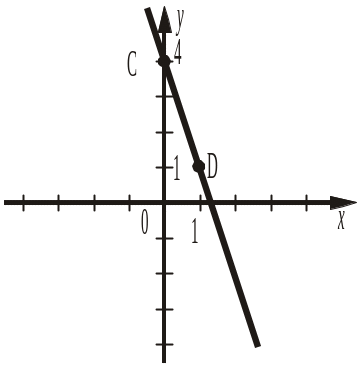
2. Побудувати графік рівняння 3x + y = 4.

1) Виразимо змінну y через змінну x: y = –3x + 4.

2) Знаходимо два розв’язки рівняння. Нехай x = 0, тоді y = –3 · 0 + 4 = 4; y = 4; розв’язок (0; 4); нехай x = 1, тоді y = –3 · 1 + 4 = –3 + 4 = 1; y = 1; розв’язок (1; 1).

2) Будуємо на координатній площині точки C(0; 4) і D(1; 1).

3) Проводимо пряму СD (рис. 24). Дана пряма є графіком рівняння 3x + y = 4.

Рис. 23	Рис. 24

Графіком лінійного рівняння ax + by = 0, де a  0 і b  0, або рівняння виду y = kx є пряма, яка проходить через початок координат.