Статистика
SWP
имеет широкий набор средств для решения
различных статистических задач. Прежде
всего, позволяет вычислить различные
параметры выборок. Среднее арифметическое
(выборочная средняя) вычисляется командой
Compute/Statistics/Mean,
среднее
геометрическое - Compute/Statistics/Geometric
Mean,
cреднее
гармоническое - командой
Compute/Statistics/Harmonic
Mean,
среднее
отклонение
- Compute/Statistics/Mean
Deviation,
среднее
квадратическое
отклонение - Compute/Statistics/Standart
Deviation.
При
этом данные можно ввести в виде списка,
перечислив их через запятую или заполнить
ими матрицу. Для матриц все эти оценки
будут считаться по отдельности для
каждой строки и представлять собой
список. Можно
вновь посчитать оценку для полученного
списка и найти интересующее нас
значение параметра выборки. Элементами
списка или матрицы могут быть не только
числовые данные, но и просто имена
переменных. При этом если первая строка
матрицы состоит из не определенных
ранее буквенных символов, то система
трактует их как названия данных и не
учитывает в расчетах. Например, для
списка значений (15,18,19,16,16), вычисляя
среднее арифметическое, получим
Mean(s)=16,8,
а для матрицы
Mean(s)=
.
Кроме этих параметров можно найти значение квантилей с помощью команды Compute/Statistics/Quantile..., задав после данных значение квантиля в процентах в виде десятичной дроби в диапазоне [0;1]. Также система позволяет вычислить значения моментов различных порядков с помощью пункта Compute/Statistics/Moment... После выбора этого пункта появляется диалоговое окно, где необходимо задать порядок момента в поле Moment number и выбрать число, относительно которого считается момент в поле Moment Origin, выбрав либо пункт About mean для вычисления центрального момента, либо пункт About для вычисления момента относительно другой точки. В последнем случае для этой величины имеется специальное окошко, в которое ее необходимо ввести, например, для вычисления начального момента следует ввести нуль. Ниже приведены примеры вычисления квантилей и моментов:
B=(15,18,19,16,16), 0.6th Quantile(s): 17
Moment number:2, Moment Origin: About Mean
B, Moment(s): 2. 16
Moment number:2, Moment Origin: About 0
B, Moment(s): 284.4
Система
SWP
также позволяет проводить корреляционный
анализ. В справочной системе указано,
что корреляционную матрицу можно
получить, выбрав пункт
Compute/Statistics/Correlation.
При этом если в качестве исходных данных
была введена матрица m*n,
то корреляционная матрица будет содержать
коэффициенты корреляции для каждой
пары столбцов, она будет симметричной
и на ее главной диагонали будут единицы.
Однако, попытки вычислить корреляционную
матрицу на практике успехом не увенчались.
Ковариационная матрица вычисляется
при выборе пункта Compute/Statistics/Covariance.
Элементы корреляционной матрицы можно
получить из соответствующих элементов
ковариационной матрицы делением на
произведение среднеквадратических
отклонений. Например, для матрицы
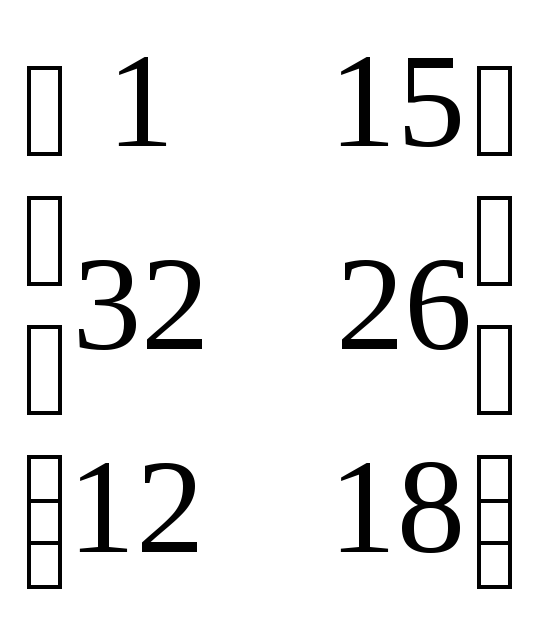были получены следующие результаты:Correlation
matrix:
undecidable
Covariance
matrix:
Standard deviation(s): [15.177, 5.6862]
Для
построения линий регрессии используется
пункт меню Compute/Statistics/Fit
Curve to Data...
При
выборе этого пункта появляется диалоговое
окно, в котором надо задать следующие
параметры: Location
of
dependent
variable
– местонахождение зависимой переменной,
надо выбрать в каком столбце (первом
или последнем) находится зависимая
переменная; после этого следует выбрать
тип регрессии, возможны три варианта.
Первый – это линейная регрессия для
выбранной зависимой переменной плюс
константа, второй – то же самое, но без
константы, и третий – это полиномиальная
регрессия, в этом случае необходимо еще
указать порядок полинома. Для каждого
из этих случаев следует выбрать в
диалоговом окне соответственно пункты
Multiple
Regression/Multiple
Regression
(No
Constant)/Polynomial
of
Degree.
Результат будет получен в виде уравнения,
в котором зависимая переменная будет
выражена через остальные. В противном
случае система не производит никаких
вычислений. Например, для матрицы
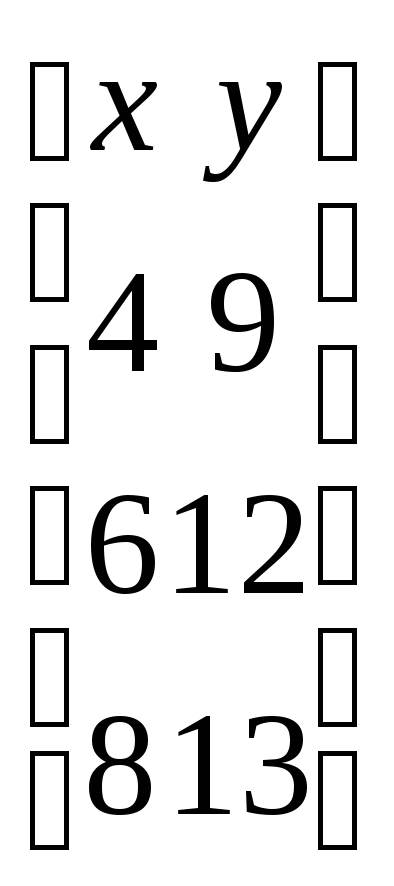
Location of dependent variable:last column
Multiple Regression
был
получен результат
.
Необходимо помнить, что при задании данных в виде матрицы столбцы обязательно должны быть помечены буквенными идентификаторами, то есть первая строка матрицы должна содержать имена переменных.
Наконец, с помощью системы SWP можно получить случайные числа с заданным законом распределения. Для этого выбираем пункт Compute/Statistics/Random Numbers, после чего появится диалоговое окно. В поле с названием How many? следует отметить количество требуемых чисел, затем выбрать закон распределения из списка Distribution. Список содержит следующие законы: бэта, биномиальный, Коши, хи-квадрат, показательный, F-распределение, гамма-распределение, нормальное, Пуассона, Стьюдента, равномерное и Вэйбулла. После выбора закона распределения, система предложит указать параметры, например, число степеней свободы для хи-квадрат или математическое ожидание и среднеквадратическое отклонение для нормального. Примеры:
How many? 10
Distribution: normal
Mean: 5
Standart deviation: 1
5. 8109, 6. 0778, 4. 4986, 5. 5616, 3. 9685, 5. 1515, 5. 859, 4. 8436,
7.2132, 6. 0683
How many? 10
Distribution: uniform
Lower end of range:0
Upper end of range:100
27.765, 96.22, 98.137, 25.519, 89.154, 95.907, 47.533, 97.214, 9. 508, 37. 225
Следует иметь в виду, что статистические возможности SWP уступают возможностям специализированных статистических пакетов, таких, как Statistics или SPSS.