3.2 Вероятность как нормированная мера

Определение 11.

Пусть Ω— некоторое множество иΨ—σ-алгебра его подмножеств. Функцияμ: Ψ → R U {∞}называетсямеройна(Ω, Ψ), если она удовлетворяет условиям:

(M1) Для любого множестваА Ψего мера неотрицательна:μ(А)≥ 0.

(M2) Для любого счетного набора попарно непересекающихся множествА₁, А₂… Ψмера их объединения равна сумме их мер:

(«счетная аддитивность» или «σ-аддитивность»). Иначе говоря, мера есть неотрицательная, счетно-аддитивная функция множеств.

Определение 12.

Пусть Ω— некоторое множество иΨ—σ -алгебра его подмножеств. Мераμ: Ψ → R называетсянормированной, еслиμ(Ω) = 1. Другое название нормированной меры — «вероятность» или «вероятностная мера».

То же самое еще раз и подробно:

Определение 13.

Пусть Ω— пространство элементарных исходов иΨ—σ-алгебра его подмножеств (событий).Вероятностьюиливероятностной меройна(Ω, Ψ), называется функцияP Ψ → R, обладающая свойствами:

(P1) Для любого событияА Ψвыполняется неравенствоP(А)≥ 0;

(P2) Для любого счетного набора попарно несовместных событийА₁, А₂… Ψимеет место равенство

(P3) Вероятность достоверного события равна единице: P(Ω) = 1.

Свойства (P1)–(P3) часто называют «аксиомами вероятности».

Определение 14.

Тройка (Ω, Ψ,Р), в которойΩ— пространство элементарных исходов,Ψ—σ-алгебра его подмножеств иP— вероятностная мера наΨ, называетсявероятностным пространством.

Выпишем свойства вероятности:

0. 

1. Для любого конечного набора попарно несовместимых событий А₁, А₂…  Ψ имеет место равенство

0. 

1. Если , то

2. Если , то

3. 

4. 

5. 

6. 

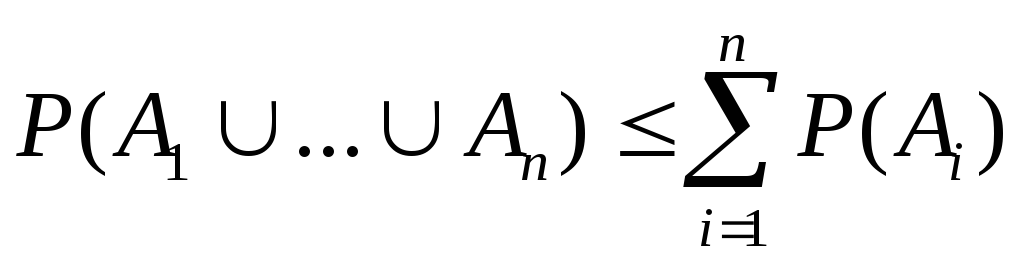
7. (2)

Раздел 4. Условная вероятность, независимость

4.1 Условная вероятность

Пример 13. Кубик подбрасывается один раз. Известно, что выпало более трех очков. Какова при этом вероятность того, что выпало четное число очков?

В данном случае пространство элементарных исходов состоит из трех равновозможных элементарных исходов: Ω = {4, 5, 6}, и событиюA = {выпало четное число очков}благоприятствуют 2 из них:A = {4, 6}. ПоэтомуP(A) = 2/3.

Посмотрим на этот вопрос с точки зрения первоначального эксперимента. Пространство элементарных исходов при одном подбрасывании кубика состоит из шести точек: Ω = {1, 2, 3, 4, 5, 6}. Слова «известно, что выпало более трех очков» означают, что в эксперименте произошло событиеB = {4, 5, 6},. Слова «какова при этом вероятность того, что выпало четное число очков?» означают, что нас интересует, в какой доле случаев при осуществленииBпроисходит иА. Вероятность событияА, вычисленную в предположении, что нечто о результате эксперимента уже известно (событиеBпроизошло), мы будем обозначать черезP(A/B)

Мы хотим вычислить отношение числа исходов, благоприятствующихАвнутриB(то есть благоприятствующих одновременноA иB), к числу исходов, благоприятствующихB.

Определение 15. Условной вероятностью событияА, при условии, что произошло событиеВ, называется число

Будем считать, что условная вероятность определена только в случае, когда P(В) > 0.

Следующее свойство называется "теоремой умножения":

Теорема 6.P(A∩B) = P(B)P(A\B) = P(A)P(B\A),если соответствующие условные вероятности определены (то есть еслиP(В) > 0, P(A) > 0).

Теорема умножения для большего числа событий:

Теорема 7. P(A₁ ∩ A₂ ∩…∩ A_n) = P(A₁) P(A₂\A₁) P(A₃ \A₁ ∩A₂)… P(A_n \A₁∩…∩A_n-1)если соответствующие условные вероятности определены.