5.6 Теорема Пуассона для схемы Бернулли

Предположим, нам нужна вероятность получить не менее десяти успехов в 1000 испытаний схемы Бернулли с вероятностью успеха 0.003. Вероятность этого события равна любому из следующих выражений:

и вычисление даже одного слагаемого в каждом из этих выражений весьма проблематично.

Сформулируем теорему о приближенном вычислении вероятности какого-либо числа успехов в большом числе испытаний схемы Бернулли с маленькой вероятностью успеха. Термин «большое число» должен означать n → ∞. Если при этомp = p_n→ 0,то, очевидно, вероятность получить любое конечное число успехов при растущем числе испытаний стремится к нулю. Необходимо чтобы вероятность успехаp = p_n→ 0одновременно с ростом числа испытаний. Но от испытания к испытанию вероятность успеха меняться не может (см. определение схемы Бернулли).

Поэтому рассмотрим «схему серий»: есть

одно испытание ○ с вероятностью успеха p₁

два испытания ○ , ○ с вероятностью успеха p₂

…

n испытаний ○ , … , ○ с вероятностью успеха p_n

…

Вероятность успеха меняется не внутри одной серии испытаний, а от серии к серии, когда меняется общее число испытаний. Обозначим через v_n число успехов в n-той серии испытаний.

Теорема 17(Теорема Пуассона).

Пусть n → ∞,p_n→ 0так, чтоn p_n→ λ > 0. Тогда для любогоk ≥ 0вероятность получитьkуспехов вn испытаниях схемы Бернулли с вероятностью успехаp_nстремится к величине

(5)

для n → ∞,p_n→ 0 так, чтоn p_n→ λ

Определение 22.Пустьλ > 0— некоторая постоянная. Набор чисел называетсяраспределением Пуассона с параметром λ.

Пользуясь теоремой 17, можно приближенно посчитать вероятность получить не менее десяти успехов в 1000 испытаний схемы Бернулли с вероятностью успеха 0.003, с вычисления которой мы начали. Поскольку n = 1000«велико», аp_n= 0.003 «мало», то, взявλ = n p_n= 3 , можно написать приближенное равенство

(6)

Осталось решить, а достаточно ли n=10³«велико», аp_n= 0.003«мало», чтобы заменить точную вероятностьP(v_n = k) на приближенное значение

Для этого нужно уметь оценивать разницу между этими двумя вероятностями.

Теорема 18(Теорема Пуассона с оценкой погрешности).

Пусть A  {0, 1, …, n}— произвольное множество целых неотрицательных чисел,v_n— число успехов вnиспытаниях схемы Бернулли с вероятностью успехаp, λ = n p. Тогда

Таким образом, теорема 18 предоставляет нам возможность самим решать, достаточно ли n«велико», аp«мало», руководствуясь полученной величиной погрешности.

Какова же погрешность в формуле (6)?

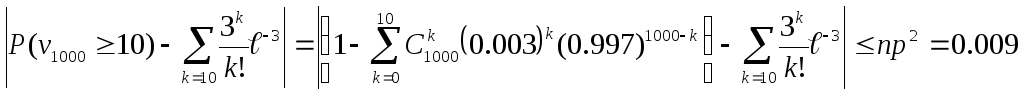
Погрешность не более 0,009 (при вероятности около 0,001). Во всяком случае, можно утверждать, что искомая вероятность никак не больше, чем 0,01=0,001+0,009.

Рассмотрим еще одну формулу приближенного вычисления p_n(m) когдаnвелико. В отличии от предыдущего результата число успеховmв этом случае тоже растет с ростомn, а вероятность успеха постоянна.

Локальная теорема Муавра – Лапласа

Пусть .Предположим, чтои величиныявляются ограниченными. Тогда