Гипергеометрическое распределение

Пример 7.

Из урны, в которойn₁белых иn -n₁чёрных шаров, наудачу, без возвращения вынимаютk шаров,k<n. Термин «наудачу» означает, что появление любого набора изk шаров равно возможно. Найти вероятность того, что будет выбрано ровноk₁белых иk - k₁чёрных шаров.

Заметим, что при k₁ > n₁илиk - k₁ > n - n₁искомая вероятность равна 0, так как соответствующее событие невозможно. Пустьk₁ < n₁иk - k₁ < n - n₁. Результатом эксперимента является набор изkшаров. При этом можно не учитывать или учитывать порядок следования шаров.

1.Выбор без учета порядка. Общее число элементарных исходов есть числоk–элементных подмножеств множества, состоящего изnэлементов, то есть(по теореме 3).

Обозначим через Aсобытие, вероятность которого требуется найти. СобытиюA благоприятствует появление любого набора, содержащегоk₁белых шаров иk - k₁черных.

Число благоприятных исходов равно произведению (по теореме 1) числа способов выбрать k₁белых шаров изn₁и числа способов выбратьk - k₁черных шаров изn - n₁:

Вероятность событияAравна:

2.Выбор с учетом порядка. Общее число элементарных исходов есть число способов разместитьnэлементов наkместах(по теореме 2).

П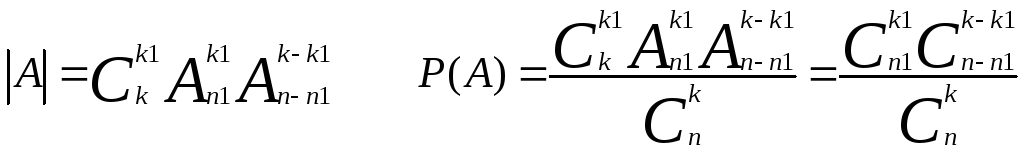ри подсчете числа благоприятных исходов нужно учесть, как число способов выбрать нужное число шаров, так и число способов расположить эти шары средиk. Можно, скажем, посчитать число способов выбратьk₁ мест средиk(равное), затем число способов разместить на этихk₁местахn₁белых шаров (равное— не забывайте про учет порядка!), и затем число способов разместить на оставшихсяk - k₁местахn - n₁черных шаров (равное). Перемножив эти числа, получим:

Врассмотренной задаче мы сопоставили каждому набору изk₁белых иk-k₁черных шаров вероятность получить этот набор при выбореkшаров из урны, содержащейn₁белых иn-n₁черных шаров:

Определение 8. Соответствие или следующий набор вероятностей

Называется гипергеометрическим распределением.

Раздел 2. Геометрическая вероятность

2.1 Что это такое

Рассмотрим какую-нибудь областьΩвR^m,(на прямой, на плоскости, в пространстве). Предположим, что «мера»Ω(длина, площадь, объем, соответственно) конечна. Пусть случайный эксперимент состоит в том, что мы наудачу бросаем в эту область точкуа. Термин «наудачу» здесь означает, что вероятность попадания точки в любую частьА  Ωне зависит от формы или расположенияА внутриΩ, а зависит лишь от «меры» области.

Определение 9. Эксперимент удовлетворяет условиям «геометрического определения вероятности», если его исходыможноизобразить точками некоторой областиΩвR^mтак, что вероятность попадания точки в любуюА  Ωне зависит от формы или расположенияА внутриΩ, а зависит лишь от меры областиА (и, следовательно, пропорциональна этой мере):

«Мерой» мы пока будем называть длину, площадь, объем и т.д.

Если для точки, брошенной в область Ω, выполнены условия геометрического определения вероятности, то говорят, что точкаравномерно распределена в области Ω.

Пример 8. Точка наудачу бросается на отрезок [0,1]. Вероятность точке попасть в точку {0,5} равна нулю, так как мера множества, состоящего из одной точки («длина точки»), есть 0. Вместе с тем попадание в точку {0,5} не является невозможным событием — это один из элементарных исходов эксперимента.