13.2 Неравенства Чебышёва

Все неравенства в этом параграфе принято относить к одному классу, называемому «неравенствами Чебышёва». Следующее неравенство часто называют собственно неравенством Чебышёва, хотя в такой форме оно появилось впервые, видимо, в работах А. А. Маркова (например, Исчисление вероятностей, 1913 г.).

Теорема 27(Неравенство Маркова).

Если , то для любого положительногоx

Доказательство.Введем новую случайную величинуξ_x, называемую «срезкой» с. в.ξна уровнеx:

Для неё и,

1.

2.

Нам потребуется следующее понятие.

Определение 48. ПустьA— некоторое событие. Назовеминдикатором события A случайную величинуI(A), равную единице, если событиеAпроизошло, и нулю, еслиA не произошло.

По определению, I(A)имеет распределение Бернулли с параметромp = P(I(A) = 1) = P(A), и ее математическое ожидание равно вероятности успехаp = P(A).

Случайную величину ξ_хможно представить в виде

Тогда

(11)

Вспомним, что , и оценим снизу согласно (11):

Итак, , что и требовалось доказать.

Следующее неравенство мы будем называть «обобщенным неравенством Чебышёва».

Следствие 12. Пусть функцияgмонотонно возрастает и неотрицательна на[0,]. Если , то для любого положительногох

В 1853 г. И. Бьенеме (I. Bienayme) и в 1866 г., независимо от него, П. Л. Чебышёв прямыми методами доказали следующее неравенство

Следствие 13(Неравенство Чебышёва-Бьенеме). Если , то

В качестве следствия получим так называемое «правило трех сигм», которое формулируют, например, так: вероятность случайной величине отличаться от своего математического ожидания более, чем на три корня из дисперсии, мала. Разумеется, для каждого распределения величина этой вероятности своя: для нормального распределения, например, эта вероятность равна 0,0027 — см. свойство9. Мы получим верную для всех распределений с конечной дисперсией оценку сверху для «вероятности с. в. отличаться от своего математического ожидания более, чем на три корня из дисперсии».

Следствие 14. Если , то

13.3 Законы больших чисел

Определение 49. Говорят, что последовательность с. в.с конечными первыми моментамиудовлетворяет закону больших чисел(ЗБЧ), если

(12)

Законами больших чисел принято называть утверждения об условиях, при которых последовательность с. в. «удовлетворяет закону больших чисел».

Выясним сначала, что означает и когда выполнен ЗБЧ для независимых и одинаково распределенных с.в.

Заметим, что если с. в. одинакого распределены, то математические ожидания у них одинаковы (и равны, например,), поэтому (12) можно записать в виде

Итак, законы больших чисел.

Теорема 28(ЗБЧ в форме Чебышёва).

Для любойпоследовательности независимых и одинаково распределенных случайных величин с конечным вторым моментом имеет место сходимость:

ЗБЧ утверждает, что среднее арифметическое большого числа случайных слагаемых «стабилизируется» с ростом этого числа. Как бы сильно каждая с. в. не отклонялась от своего среднего значения, при суммировании эти отклонения «взаимно гасятся», так что среднее арифметическое приближается к постоянной величине.

В дальнейшем мы увидим, что требование конечности второго момента (или дисперсии) связано исключительно со способом доказательства, и что утверждение остается верным если требовать существования только первого момента.

Доказательство. Обозначим черезсумму первыхn с. в., а их среднее арифметическое через. Тогда

Пусть ε > 0. Воспользуемся неравенством Чебышёва (следствие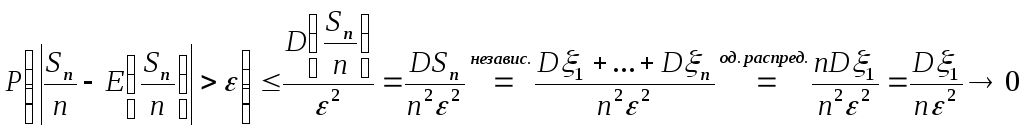13):

(13)

при , поскольку, по условию, конечна.

Следствие 15. Последовательность с. в.с конечными вторыми моментами удовлетворяет ЗБЧ, то есть

при выполнении любого из следующих условий:

а) если , то естьпри;

б) если независимы и, то есть

в) если независимы, одинаково распределены и имеют конечную дисперсию (ЗБЧ Чебышёва).

Теорема 29(ЗБЧ в форме Хинчина).

Для любой последовательности независимых и одинаково распределенных случайных величин с конечным первыммоментом имеет место сходимость:

Более того, в условиях теоремы 29имеет место сходимость «почти наверное». Получим в качестве следствия из ЗБЧ Чебышёва закон больших чисел Я. Бернулли (1713). В отличие от доказанного через полтора столетия ЗБЧ Чебышёва, описывающего предельное поведение среднего арифметического с. в. спроизвольнымираспределениями, ЗБЧ Бернулли — утверждение только длясхемы Бернулли.

Теорема 30(ЗБЧ Бернулли).

Пусть А— событие, которое может произойти в любом изnнезависимых испытаний с одной и той же вероятностьюP(А). Пустьv_n(А)— число осуществлений событияАвnиспытаниях. Тогда

При этом для любого ε > 0