
Теоретическая механика (фундаментальные законы механики). Учебное пособие
.pdf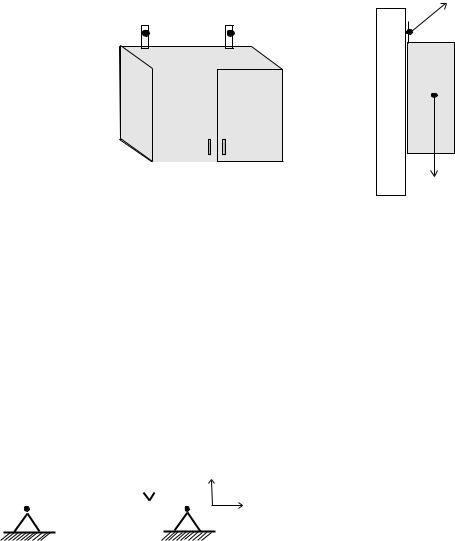
32 |
Глава 1. Законы равновесия тел |
|
|
aa |
R |
|
aaa |
||
|
||
aaa |
|
|
aaa |
|
|
aaa |
|
|
aaa |
|
|
aaa |
|
|
aaa C |
|
|
aaa |
|
|
aaa |
|
|
aaa |
|
|
aaa |
|
|
aaa |
|
|
aaaaaa G |
||
aaa |
|
|
Рис. 1.6. Навесной кухонный шкаф
на расстоянии 25 см от стены. Вычислить силу, действующую на каждый шуруп. Особое внимание обратить на составляющую силы, которая вытягивает шуруп из стены.
1.6.Иллюстративные задачи
Задача 1: шарнирно опертая балка, нагруженная силой. Рассмотрим задачу, изображенную на рис. 1.7.
|
A |
|
P |
j |
В качестве тела A примем саму рассмат- |
|
|
|
|||||
|
|
|
|
|
i |
риваемую балку. Левую опору, закреплен- |
|
|
|
|
|
||
|
|
|
|
|
||
|
B |
|
C |
ную от смещений, примем за тело B. Эта |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
опора препятствует смещениям балки, но |
Рис. 1.7. Нагружение балки силой |
не препятствует поворотам балки вокруг |
|||||
|
|
|
|
|
|
точки соединения балки с опорой. Правую |
опору балки примем за тело C. Эта опора препятствует вертикальным смещениям правого торца балки, но не препятствует горизонтальным смещениям балки и поворотам балки вокруг точки соединения правого конца балки с правой опорой. Наконец, в качестве тела P будем считать некое устройство, воздействие которого на тело A сводится к силе P. Запишем первый закон статики
F(A, Ae) = F(A, B) + F(A, C) + F(A, P) = F(A, B) + F(A, C) − Pj = 0. (1.6.1)
Поскольку правая опора C не препятствует смещению балки вдоль горизонтальной оси, то имеем ограничение
F(A, C) · i = 0 F(A, C) = FCj. |
(1.6.2) |
Уравнение (1.6.1) содержит два неизвестных вектора. Поэтому необходимо использовать дополнительное уравнение, роль которого исполняет второй

1.6. Иллюстративные задачи |
33 |
|
|
закон статики.
MQ(A, Ae) = MQ(A, B) + MQ(A, C) + MQ(A, P) = 0. |
(1.6.3) |
В качестве опорной точки Q выберем точку контакта левой опоры с балкой. С этой же точкой совместим начало в системе отсчета. Тогда имеем RQ = 0. Моменты необходимо вычислять по формуле (1.1.3). В рассматриваемой задаче для каждого из моментов1, входящих в (1.6.3), точки приведения можно выбрать так, чтобы собственно моменты обращались в нулевые. Для момента MQ(A, B) точку приведения выбираем на левой опоре. Для момента MQ(A, C) точку приведения выбираем на правой опоре. Наконец, для момента MQ(A, P) точку приведения выбираем в точке касания устройства, создающего силу P,
сбалкой. В таком случае имеем выражения
MQ(A, B) = 0, MQ(A, C) = l i × F(A, C) = l FC i × j,
MQ(A, P) = ai × (− P j), (1.6.4)
где l — расстояние между опорами, a — расстояние от левой опоры до “точки приложения” силы P.
При вычислении момента MQ(A, C) использовано уравнение (1.6.2). Подставляя выражения (1.6.4) в уравнение (1.6.3), получаем
l FC = a P |
F(A, B) = − |
l − a |
P j, |
F(A, C) = |
a |
P j. |
|
|
|
|
|||||
l |
l |
||||||
Задача 2: балка, опирающаяся на гладкую опору.
Рассмотрим конструкцию, изображенную на |
P |
||||||||
рис. 1.8. Левый конец однородной балки дли- |
|
||||||||
ной 2l шарнирно закреплен в точке O, которую |
C |
||||||||
совместим с началом в системе отсчета. Эту же |
h B |
||||||||
точку O выберем в качестве опорной точки, т.е. |
O a |
||||||||
RQ = RO = 0. Балку считаем телом A. Опору |
|||||||||
|
|||||||||
считаем телом O. Угловую стенку, отстоящую от |
Рис. 1.8. Балка на гладкой |
||||||||
точки O на расстоянии a и имеющую высоту |
опоре |
||||||||
h считаем телом |
B |
. При этом выполнено нера- |
|
||||||
, |
2 |
+ h |
2 |
|
2 |
. Наконец, Землю обозначаем телом E. Балку считаем |
|||
венство a |
|
|
< 4 l |
||||||
идеально гладкой, т.е. трение между балкой и угловой стенкой пренебрегаем. Выпишем первый закон статики и воспользуемся аксиомой аддитивности
F(A, Ae) = F(A, O) + F(A, B) + F(A, E) = F(A, O) + P − mg j = 0, (1.6.5) где m есть масса балки. Пусть единичный вектор e направлен вдоль балки.
1За исключением момента MQ(A, Ae).

34 |
Глава 1. Законы равновесия тел |
|
|
Поскольку балка идеально гладкая, то сила F(A, B) = P удовлетворяет условию
P · e = 0 P = P (i × j) × e,
где вектор (i × j) × e есть вектор единичной нормали к балке, а P есть величина реакции угловой стенки.
Теперь первый закон статики (1.6.5) дает
F(A, O) = mg j − P (i × j) × e. |
(1.6.6) |
Осталось определить величину реакции P. С этой целью выпишем второй закон статики
MO(A, Ae) = MO(A, O) + MO(A, B) + MO(A, E) = 0. |
(1.6.7) |
Чтобы вычислить моменты, входящие в (1.6.7), нужно воспользоваться определением момента (1.1.3). Напомним, что точку приведения для каждого из этих моментов можно выбирать произвольно. Более того, в данной задаче точки приведения можно выбрать так, чтобы собственно моменты обращались в нулевые. Легко получаются выражения
MO(A, O) = RO × F(A, O) = 0, |
MO(A, E) = −mgl e × j = − |
mgal |
||
√ |
|
k, |
||
a2 + h2 |
||||
p p
MO(A, B) = P a2 + h2e × [(i × j) × e] = P a2 + h2 k,
√
где l — расстояние от точки O до центра масс C балки, a2 + h2 — расстояние от точки O до точки контакта балки с угловой стенкой, k = i × j.
Подставляя эти равенства в (1.6.7), получаем уравнения для нахождения реакции P
|
|
P = |
mgal |
|
|
|
|||
|
|
|
. |
|
|
|
|
||
|
a2 + h2 |
|
|
|
|||||
Выражение (1.6.6) принимает вид |
|
j + √a2 |
|
+ h2 i |
|
||||
F(A, O) = mg |
1 − √a2 + h2 a2 |
+ h2 |
+ h2 a2 |
. (1.6.8) |
|||||
|
|
l |
a2 |
|
|
|
l |
ah |
|
Упражнение: проанализировать выражение для реакции в опоре (1.6.8) и объяснить почему вертикальная составляющая реакции меняет знак при некоторых значениях параметров.
Задача 3: консольная балка, нагруженная на конце.
Консольные балки часто встречаются на практике, поэтому умение вычислять силы и моменты в такого рода ситуациях оказывается необходимым. Рассмотрим простую задачу, представленную на рис. 1.9. В качестве тела A

1.6. Иллюстративные задачи |
35 |
|
|
выбираем саму балку. В качестве тела B выбираем заделку на левом конце балки. Наконец, в качестве тела C выбираем подвешенный на левом торце балки груз на нити. Балку считаем невесомой. Первый закон статики в данном случае принимает вид
F(A, Ae) = F(A, B) + F(A, C) = F(A, B) − mgj = 0 F(A, B) = mgj.
O |
l |
mg
Рис. 1.9. Консольная балка
(1.6.9) Таким образом, реакция в заделке определена.
Чтобы определить момент, действующий в заделке, необходимо воспользоваться вторым законом статики
MQ(A, Ae) = MQ(A, B) + MQ(A, C) = 0. (1.6.10)
Опорную точку Q выберем на левом торце балки и там же поместим начало в системе отсчета, т.е. RQ = 0. Тогда получим
MQ(A, B) = RP × F(A, B) + LP(A, B).
Нетрудно убедиться, что при любом выборе точки приведения P собственно момент LP(A, B) отличен от нуля. Выберем точку приведения так, что RP =
RQ = 0. Тогда имеем
MQ(A, B) = LQ(A, B).
Для момента MQ(A, C) точку приведения выберем на правом торце балки. Тогда собственно момент LC(A, C) будет равняться нулю. Получаем
MQ(A, C) = RC × F(A, C) = li × −(mgj) = −mgl i × j.
Используя последние два равенства и второй закон статики (1.6.10), полу-
чаем моментную реакцию в заделке |
|
MQ(A, B) = mgl i × j. |
(1.6.11) |
Задача решена. При этом видим, что воздействие заделки на балку, т.е. реакция заделки, выражается как силой, так моментом. Заметим, однако, что здесь момент выражается как момент силы, т.е. понятие, существовавшее в ньютоновой механике.
Задача 4: нагруженный элемент фермы.
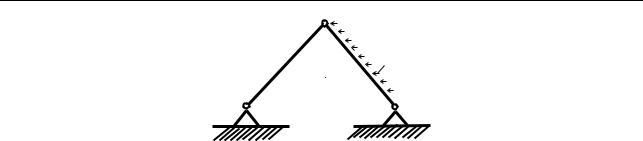
Фермами называют стержневые системы, состоящие из большого числа прямолинейных стержней. Фермы часто встречаются на практике. На рис. 1.10 представлен типичный элемент фермы, состоящий всего из двух стержней, нагруженный горизонтальной силой Qi, приложенной в точке O. Здесь мы пользуемся упрощенной терминологией, которая часто оказывается удобной.

36 |
Глава 1. Законы равновесия тел |
|
|
O
Qi
BC
F G
Рис. 1.10. Элемент фермы
Точнее было бы выразиться следующим образом. Воздействие на элемент фермы является чисто силовым, если в качестве точки приведения выбрать точку O. Решение этой простой задачи включает использование полезного приема, когда уравнения статики приходится записывать не только для всего тела, но и для тел, составляющих рассматриваемое тело. В качестве тела A выбираем конструкцию из соединенных между собой стержней B и C, длина которых одинакова и равна l. Шарнирное соединение O позволяет стержням B и C свободно поворачиваться относительно друг друга. Стержни шарнирно закреплены в точках F и G, расстояние между которыми равно a. Начало системы отсчета разместим в точке F. При вычислении моментов опорную точку выбираем также в точке F и в дальнейшем это обстоятельство не отмечаем. Кроме того, примем обозначение RO = le, где e есть единичный вектор, направленный вдоль левого стержня. Выпишем уравнения статики для тела A, которые имеют вид
F(A, Ae) = F(A, F) + F(A, G) + Q i = 0, |
(1.6.12) |
M(A, Ae) = ai × F(A, G) + l e × Q i = i × (aF(A, G) − lQ e) = 0. |
(1.6.13) |
Получили два векторных уравнения (1.6.12) и (1.6.13) для двух неизвестных векторов F(A, F) и F(A, G). Тем не менее, этих уравнений недостаточно, ибо уравнение (1.6.13) эквивалентно всего одному скалярному уравнению и не позволяет найти проекцию F(A, G) на вектор i. Однако уравнение (1.6.13) позволяет написать равенство
F(A, G) = lQa e + µ i,
где µ есть произвольный скаляр.
Чтобы полностью решить задачу, необходимо разделить все тело на отдельные элементы и уже для них выписать уравнения статики. Подобный прием встречается очень часто. Например, для деформируемых тел приходится записывать уравнения статики для бесконечно малых частей тела.
1.6. Иллюстративные задачи |
37 |
|
|
В данной задаче достаточно записать уравнения статики для стержня B. При этом будем считать, что сила Q i приложена к стержню C бесконечно близко к точке O.
Упражнение: убедиться, что решение задачи не изменится, если силу Q i считать приложенной к кончику стержня B или к шарниру O.
Уравнения статики для стержня B имеют вид
F(B, F) + F(B, C) = 0, le × F(B, C) = 0 F(B, F) = F(A, F) = λe.
Сучетом вышеприведенных равенств уравнение (1.6.12) принимает вид
|
lQ |
|
|
|
|
|
lQ |
|
|
||
λ + |
|
|
e + (λ + Q) i = 0 |
λ = − |
|
, µ = −Q. |
|
||||
a |
a |
|
|||||||||
Используя эти формулы окончательно получаем |
|
|
|||||||||
F(B, F) = − |
lQ |
e, |
F(C, G) = |
lQ |
m, |
l m = l e − a i, |
(1.6.14) |
||||
|
|
||||||||||
|
|
|
a |
|
a |
|
|
|
|
||
где m есть единичный вектор, направленный вдоль стержня C к точке O. Нетрудно убедиться, что усилия в обоих стержнях направлены вдоль стерж-
ней. Собственно, именно это обстоятельство и является главным достоинством ферм, поскольку стержни хорошо работают на растяжение-сжатие. Проиллюстрируем сказанное на примере стержня B.
Прежде всего, необходимо обратить внимание на то, что в уравнения статики для всего тела A входят только внешние воздействия, т.е. сила Q i, а также реакции опор F(A, F) и F(A, G). Знание реакций, конечно, необходимо, но сами по себе они не позволяют судить о силах, передаваемых каждым из стержней. Чтобы найти силы, передаваемые стержнями, или, что то же самое, внутренние усилия в стержнях, будем поступать следующим образом. Мысленно разделим стержень B на две части B1 и B2 так, что B = B1 B2. Через s1 обозначим расстояние от опоры F до конца стержня B1, т.е. s1 — это длина стержня B1. Сила F(B1, B2) моделирует силовое воздействие стержня B2 на стержень B1. Момент MF(B1, B2), вычисленный относительно опорной точки F, моделирует моментное воздействие стержня B2 на стержень B1. Он вычисляется по формуле
MF(B1, B2) = s1e × F(B1, B2) + L(B1, B2),
где в качестве точки приведения выбрана точка s1e. Выпишем уравнения статики для стержня B1
F(B1, Be1) = F(B1, B2) + F(B1, F) = 0,

38 Глава 1. Законы равновесия тел
MF(B1, Be1) = MF(B1, F) + MF(B1, B2) = s1e × F(B1, B2) + L(B1, B2) = 0.
Во втором из этих равенств учтено, что MF(B1, F) = 0, поскольку опора F не создает моментного воздействия на стержень B1. Решая эту систему с учетом равенств (1.6.14), получаем для внутренних воздействий в стержне B следующие выражения
F(B1 |
, B2) = |
lQ |
e, L(B1, B2) = 0. |
|
|||
|
|
a |
|
Итак, стержень B передает только продольное усилие, т.е. усилие, направленное вдоль стержня, и не передает момента. Аналогичные рассуждения с тем же результатом могут быть применены к стержню C. В идеале ферма должна быть спроектирована так, чтобы в ее элементах, т.е. стержнях, возникали бы только продольные усилия. К сожалению, при проектировании реальной фермы проведенные нами рассуждения недостаточны. В этом легко убедиться, если проанализировать полученные выше выражения для внутренних усилий и реакций в опорах. Действительно, из выражений (1.6.14) следует, что при сколь-угодно малой силе Q модули реакций в опорах стремятся к бесконечности при a → ε, 0 < ε << 1. Иными словами, в этом случае элемент фермы разрушится при приложении сколь-угодно малой нагрузки, что, разумеется, не соответствует реальности. Причина кажущегося парадокса выявляется только при более тщательном анализе, который выходит за рамки возможностей данной главы. При решении задачи мы сделали единственное допущение. А именно, мы считали что стержни деформируются столь незначительно, что их можно считать абсолютно твердыми. Остальные рассуждения были строгими. Результат оказался абсурдным при малых a. В реальных фермах этот случай не встречается, но он дает основания для сомнений, которые при расчете ответственных конструкций, например мостов, недопустимы. Строгая постановка задачи включает в себя учет деформируемости стержней, причем все рассуждения необходимо вести в нелинейной постановке. Полученная таким образом задача допускает, как минимум, два решения, одно из которых практически совпадает с найденным выше. Далее необходимо исследовать устойчивость полученных решений. Решение, найденное выше, будет неустойчивым при малых значениях параметра a. Критическое значение a может быть найдено только в результате строгого анализа. Отметим, что при анализе этой задачи стандартные программы компьютерного моделирования окажутся беспомощными и разочаруют тех, кто возлагает слишком большие надежды на компьютер. Последний, разумеется, поможет в расчетах, но предварительный аналитический анализ задачи окажется необходимым элементом всего исследования.
Задача 5: элемент стержневой системы. Немного усложним рассмот-
1.6. Иллюстративные задачи |
39 |
||
|
O |
|
|
B |
C |
q |
|
|
|
||
F |
|
G |
|
Рис. 1.11. Элемент фермы
ренную выше задачу и нагрузим правый стержень распределенной нагрузкой
— см. рис. 1.11. Решение этой задачи почти не отличается от рассмотренной выше. В качестве тела A, как и выше выбираем конструкцию из соединенных между собой стержней B и C. Кроме того, сохраняем все принятые выше обозначения. Стержень C нагружен постоянной горизонтальной нагрузкой интенсивности q. Начало системы отсчета разместим в точке F. При вычислении моментов опорную точку выбираем в точке F. Кроме того, примем обозначение RO = le = ai+lm, где m есть единичный вектор, направленный из точки G в точку O.
Выпишем уравнения статики для тела A. |
|
|
|||
F(A, Ae) = F(A, F) + F(A, G) − qli = 0, |
|
(1.6.15) |
|||
M(A, Ae) = ai × F(A, G) − a i + 2m |
× (ql)i = i × aF(A, G) + |
2 |
m = 0. |
||
|
l |
|
|
ql2 |
|
Последнее равенство переписываем в виде |
|
|
|||
|
|
ql2 |
|
|
|
F(A, G) = − |
|
m + µ i, |
|
(1.6.16) |
|
|
|
||||
|
|
2a |
|
|
|
где µ — произвольный скаляр.
Получили два векторных уравнения (1.6.15) и (1.6.16) для двух неизвестных векторов F(A, F) и F(A, G). Чтобы полностью решить задачу, достаточно дополнительно записать уравнения статики для стержня B
F(B, F) + F(B, C) = 0, le × F(B, C) = 0 |
|
F(B, F) = λe. |
||||||||
Используя последнее выражение и равенство |
(1.6.16), уравнение (1.6.15) |
|||||||||
|
|
|||||||||
переписываем в виде |
λ − 2a m = 0. |
|||||||||
l + µ − ql i + |
||||||||||
|
λ a |
|
|
ql2 |
|
|
||||
Отсюда следует, что |
|
|
|
|
|
|
||||
|
|
λ = |
ql2 |
, |
µ = |
ql |
. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2a |
2 |
|
|
|
|||
40 |
Глава 1. Законы равновесия тел |
|
|
|
|||||
|
|
|
|
|
|
|
|
||
|
Таким образом, для реакций в опорах F и G получаем выражения |
|
|||||||
|
F(A, F) = |
ql2 |
e, |
F(A, G) = − |
ql2 |
m + |
ql |
i. |
(1.6.17) |
|
|
|
2 |
||||||
|
|
2a |
|
2a |
|
|
|||
В отличие от предыдущей задачи здесь усилие в правом стержне уже не является постоянным. Чтобы найти закон изменения усилия в стержне C, следует воспользоваться следующим приемом. Положение каждой точки стержня C будем задавать вектором
R(s) = a i + s m, 0 ≤ s ≤ l, |
(1.6.18) |
где s есть расстояние, отсчитываемое от точки G до рассматриваемой точки стержня. В качестве тела C1 рассмотрим часть стержня C, заключенную между точкой G и точкой с координатой s. Оставшуюся часть стержня C обозначим символом C2. Таким образом, имеем C = C1 C2. Выпишем два закона статики
для тела C1
F(C1, Ce1) = F(C1, G) + F(C1, C2) − qsi = 0,
MG(C1, Ce1) = sm × F(C1, C2) + L(C1, C2) − (s/2)m × (qs)i = 0,
где F(C1, C2) и L(C1, C2) суть сила и момент, с которыми тело C2 действует на тело C1, т.е. это сила и момент, действующие в сечении стержня C с
координатой s. |
|
|
|
|
|
Решая последние два уравнения, находим |
|
m × i. |
|||
F(C1, C2) = q |
s − 2 i + |
2a m, L(C1, C2) = − qs |
2 |
||
|
|
l |
ql2 |
(s − l) |
|
Видим, что, в отличие от предыдущей задачи, стержень C передает не только силу, но и момент, причем сила не направлена вдоль стержня. Стержневые системы, в которых стержни работают не только на растяжение-сжатие, но и на изгиб, не принято называть фермами.
Читателю рекомендуется самостоятельно воспроизвести все рассуждения двух последних задач и тщательно обдумать возникающие в них различия.
1.7.Равновесие нерастяжимой нити с закрепленными концами
До сих пор законы статики применялись к абсолютно твердым телам. В этом пункте мы рассмотрим тела иного типа, которые могут менять свою форму при приложении нагрузки. Основное внимание здесь следует обратить на тот факт, что сами по себе законы статики неизменны, хотя форма
1.7. Равновесие нерастяжимой нити с закрепленными концами |
41 |
|
|
их реализации будет существенно другой. Ниже будет рассмотрена задача о равновесии гибкой нерастяжимой нити с закрепленными концами. Эта задача интересна во многих отношениях. Во-первых, она важна с практической точки. Например, известна проблема прочности проводов линий высоковольтных передач. В зимних условиях эти провода нередко покрываются льдом. Кроме того, на них часто действует ветровая нагрузка. В результате провода могут разорваться, что ведет к большим материальным затратам на ремонт. Можно привести много других примеров. Во-вторых, она важна с исторической и научной точки зрения. Впервые задача о равновесии нерастяжимой нити была рассмотрена Якобом Бернулли в конце XVII века. Я. Бернулли показал (1691), что уравнения равновесия нити выражаются посредством обыкновенных дифференциальных уравнений. Это были первые дифференциальные уравнения с обыкновенными производными в истории науки. Можно достаточно убедительно показать, что именно в механике зарождались почти все разделы математики. Поэтому именно механика являлась и является поставщиком объектов и идей для математики, но не наоборот, как это многие “механики”, к сожалению, думают. Последнее обстоятельство и явилось одной из главных причин стагнации фундаментальных основ механики в последние полтора столетия, ибо путь от математики — есть путь в никуда. Математика есть язык для выражения физических идей, которые сами по себе лежат далеко за пределами
математики. |
|
|
|
|
|
Вернемся, однако, к задаче о равновесии нерастяжимой нити. |
|
|
|||
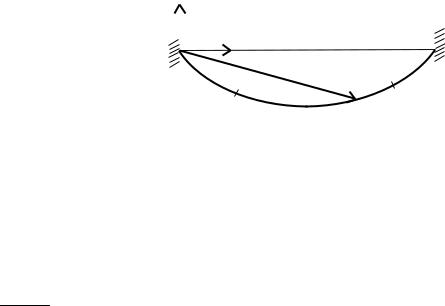
Рассмотрим тонкую нить (канат), |
|
j |
|
|
|
|
|
|
|||
закрепленную своими концами (рис. 1.12). |
i |
|
|
||
Длина нити равна l, а расстояние меж- |
|
O |
B |
|
|
|
|
|
|||
|
|
R(s) |
|
|
|
ду опорами равно a < l. Нить нагруже- |
|
|
|
|
|
|
|
s2 |
|||
|
|
||||
на собственным весом. Требуется най- |
|
s1 |
|||
|
|
|
|||
ти силу натяжения в нити и форму, ко- |
|
|
|
|
|
торую она приобретает под действием |
Рис. 1.12. Равновесная форма гибкой |
||||
сил тяжести. Начало в системе отсчета |
|
|
нити |
|
|
|
|
|
|
|
|
и опорную точку выберем на левом конце нити. Форму нити будем определять заданием вектора R(s), где параметр s : 0 ≤ s ≤ l есть расстояние, отсчитываемое вдоль нити, от левого конца нити. Вектор R(s) заранее неизвестен и подлежит определению. Введем вектор единичной касательной t к кривой R(s)
t(s) = |
dR(s) |
, |
|dR| = ds |
|t(s)| = 1. |
(1.7.1) |
ds |
Второе из уравнений (1.6.8) есть условие нерастяжимости нити. Нить будем считать однородной. Массу dm бесконечно малой части нити ds вычисляем по формуле dm = ρds, где ρ = const называется погонной плотностью массы
