Понятие рыночного портфеля ценных бумаг. Основное уравнение равновесного рынка
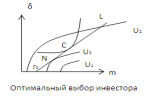
Если конкурентный рынок пребывает в равновесии, то спрос всех инвесторов по каждому активу совпадает с совокупным предложением этого актива. Соответственно каждый инвестор комплектует портфель только из долей оптимального рискового портфеля C и безрискового актива чтобы максимизировать свою уровневую доходность U. Точка N, выбранная не безразличным к риску инвестором, определяется точкой касания подходящей кривой безразличия U0 и прямой эффективных фондовых портфелей L. Точка N дает максимум полезности. (U1 неосуществима, U2 невыгодна). Выбор точки N задает пропорции деления капитала между безрисковым активом и портфелем С.
Рыночный портфель— портфель, состоящий из всех активов, доступных инвестору, причем вес каждого актива в портфеле совпадает с его долей по рынку в целом, т.е. с отношением общей рыночной стоимости этого актива к общей стоимости всех активов (т.е. рынка в целом).
Рыночный портфель отражает полученный в теории вывод, что все инвесторы разделяют свой капитал между двумя фондами: безрисковым и рыночным портфелем. При этом выбор пропорции, т.е. конкретной точки на прямолинейном участке эффективной траектории, определяется отношением к риску индивидуального инвестора.
Заметим, что данный вывод не охватывает все возможные случаи в зависимости от допустимости продаж без покрытия (short sale) и величины требуемой доходности mp. Например, при запрете подобных продаж и mp> mc эффективные портфели перейдут на криволинейный участок траектории с нулевой долей вложения в безрисковую компоненту.
Портфель рынка отражает ту же структуру, что и оптимальный (касательный) портфель, вычисленный на основе вероятностных характеристик ценных бумаг, а сам рынок имеет свойства, присущие этому оптимальному портфелю.
Модель
оценки капитальных активов
(capitalassetspricingmodel
– CAPM).
Описывает
равновесную взаимосвязь между ожидаемым
доходом
бумаги j
и ее вкладом
в риск рыночного портфеля (основное
уравнение равновесного рынка)
где коэффициент пропорциональности
называется бета вклада i-ой бумаги относительно оптимального (рыночного портфеля) (числовое значение определяет вклад данной бумаги в дисперсию (риск) рыночного портфеля). Превышение ожидаемой эффективности какой-либо рисковой бумаги или портфеля ценных бумаг над эффективностью безрискового вклада называется премией за риск.
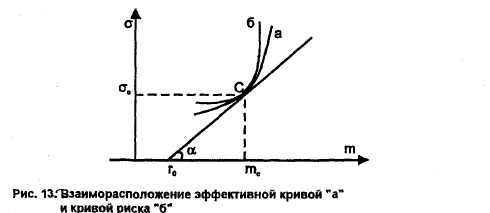
Общий, рыночный и диверсифицируемый риски финансовых активов.
Общий риск актива A , будь то ценной бумаги или портфеля, можно разделить на две части: обусловленную влиянием рыночного портфеля (конъюнктуры рынка ценных бумаг) и ту, что не зависит от рынка и связана с изменением прочих факторов:
где
– риск рыночного портфеля,
– «бета» актива А,
– рыночный (или систематический) риск
актива А,
– индивидуальный (или несистематический)
риск актива А.
Разделение риска вытекает из формулы разложения дисперсии случайной доходности актива А по влиянию доходности рыночного портфеля Rc.
D(R)=DM(R/X)+MD(R/X) (где DM(R/X) характеризует ту часть флуктуации переменного результата R, которая вызвана влияние фактора Х. Средняя условная дисперсия MD(R/X)характеризует ту часть общей дисперсии переменной R, которая вызвана совокупностью всех остальных факторов, кроме влияния переменной Х). За счет диверсификации вложения можно уменьшить индивидуальный риск, вплоть до получения сильно диверсифицированного актива, не имеющего этого риска (σA2=0) и доходность которого зависит только от рыночных ситуаций.
Рыночный портфель содержит все торгуемые на рынке бумаги, т.е. предельно диверсифицирован, и по структуре тождественен касательному портфелю C. Его риск отвечает минимальному значению критерия оптимизационной задачи и, следовательно, неуменьшаем. Согласно модели CAPM, инвесторы вознаграждаются за рыночный риск, но их нерыночный (несистематический) риск не компенсируется