54. Предикативные факторные регрессионные модели, выявление и коррекция ошибок спецификации

Предикативные модел-ие не то, что объясняет действительность, а предсказывает (предикативные модели - это модели предсказательного, прогностического характера, напр. факторные регрессионные модели, модели нейронные, деревья решений). Нейронные сети – совокупность методов поиска скрытых закономерностей в массивах данных в процессе «обучения» на примерах и ряд других методов (нейрон - простейший элемент, который выполняет вычисления и преобразование входа в выход на основе весовых коэффициентов).

Факторная регрессионная модель – статистическая зависимость 1ой переменной (зависимой) от 1ой или нескольких независимых (объясняющих) переменных. Объектно-пространственные выборки (кроссекционные данные): . Значение j-го признака, характеризующее состояние i-го объекта на фиксируемый момент времени. Общ-ий вид: y=f(Х)+ε (f(Х) неслучайная сост-щая процесса; ε–случ-ая сост-я). Если единственный аргумент – время, то модель ВР (y=f(t)+ε)

Условия клас-ой линейной модели множественной регрессии (усл-ия Гауса-Маркова): M[ε]=0 и 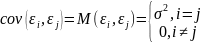(ε ≈N(0,σ²))

Случайная компонента – случ-ная величина, через кот-ую прояв-ся влияние неучтенных факторов.

Уравнение регрессии по генеральной выборке:

Уравнение регрессии по выборочным данным:

Конкретное значение: 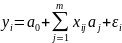, – вектор-столбец оцененных значений параметров

Критерий (д/МНК): 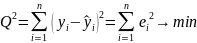(минимизируем квадрат суммы ошибок). Св-а оценк МНК: 1. Несмещенность (М(а_j)=α_j V j=1;m); 2. Состоятельность ( ) – при большом кол-ве наблюдений дисперсия оценки параметра в пределе стремится к 0. 3. Эффективность: оценка а_j=а* параметра α_j эф-на, если она имеет минимальную дисперсию, среди всех возможных оценок данного параметра.

1. Спецификация модели – представление понимания исследователями логики развития объекта изучения в форме математической модели, пригодной для дальнейших эмпирических исследований (выбор (анализ) состава независимых переменных модели и вида функций f(x), также анализ исх-ых данных с помощью тестов). 2. Идентификация параметров функции (а_j). Принцип максимального правдоподобия: наилучшим описанием явления явл-ся то, кот-ое дает наиб-ю вероятность получения в результате измерений именно тех значений, которые и будут фактически получены.(метод макс-го правд-ия и МНК д/норм-го распр-ия))

Ошибки спецификации в узком смысле – нарушения, связанные с выбором объясняющих переменных (из-за неправильной спецификации матрицы Х); 1. Игнорирование существенной переменной; 2. Вкл-ие в модель незначимой переменной, не влияющей на РП. Более широкая предполагает: 3. Ошибку в опр-ии форм зависимостей между факторами, а также оценивание ложной регрессии; 4. Параметры не укладываются в отведённые им интервалы;. 5. Мультиколлинеарность переменных (связь в матрице Х); 6. Гетероскедастичность в остатках; 7. Наличие автокорреляции остатков.

Эти ошибки обычно приводят к смещённости, несостоятельности и неэффективности оценок модели. Обнаружение ошибок: -логический анализ; -корреляционный анализ, -дисперсионный анализ; -исследовия остатков моделей (и графические, на соответствие условиям Гауса-Маркова и тп); -оценку гипотез. При этом наличие ошибок 5, 6 и 7-го видов ставит под сомнение вообще возможность испол. стандартных методов оценивания параметров регрессий. Корректировка ошибок спецификации – непременное условие повышения априорных прогностических свойств модели. При выявлении описанных ошибок необходимо уточнить спецификацию, если это не помогает, необходимо использовать специальные методы.

Мультиколлинеарность: ; R_j² – коэф-т детерминации регрессии j-ой переменной по оставшимся (m-1). Чем VIF больше 1, тем с большей вероятностью мультиколлинеарность присутствует. Методы устранения: -методы смещения параметров; -«очистка» от мультикол-ти в рамках выбранного метода, напр. МНК («Все возможные регрессии» и «Пошаговый отбор переменных»).

Гетероскедастичность: графический анализ (ось ординат e_t, абсцисс–Ŷ), если вариация остатков растет с увеличением Ŷнарушение предпосылки МНК D[ε_t]=σ². Тест ранговой корреляции Спирмэна: 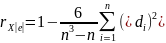, n – число ранжированных объектов; d_i– разность рангов переменой Х и абсолютной ошибки i-го наблюдения. Н0: – статистика подчинена нормальному закону распределения Стьюдента

Оценка значимости: t^табл (n-2;α); t^расч> t^табл→H₀ отвергается: есть гетероскедостичность. Если есть гетероск-сть, то уточняем спецификацию, используем специальные методы оценки: обобщенный МНК (оценки не обладают св-ом эффективности) и метод взвешенных МНК(корректируем исходную статистику на стандартное отклонение S_i, строим регрессию на полученных данных)

Автокорреляция: критерий Дарбина-Уотсона: ; DW[0;4]. Для статистики DW критических границ для заданного уровня значимости, числа наблюдений n и числа независимых переменных k: d_L и d_U.

Методы устранения: -спец-ые поправочные процедуры (напр, итеративная процедура Кохрана-Оркатта и тд); -уточнение спецификации (возможно выпал существенный фактор или вид функции f(x) неправильный); -ввод фактора времени.

57-58. Прогнозирование на основе экспертного оценивания. Специфика оценки качества экспертного прогноза: способы измерения и возможности влияния на него.

Экспертное оценивание – формализованная кач-ая или кол-ая оценка экспертами характеристик объектов. При след-их ситуациях: 1. Отсутствие статистических данных; 2. Отсутствие методологии (новое явление); 3. Высокая нестабильность системы; 4. Длительность периода либо слишком короткая (чрезвычайная ситуация) либо долгосрочное прогнозирование.

Важнейший фактор качества – эксперт. Требования: 1. Компетентность общественно признана; 2. Оценки транзитивны и устойчивы во времени (стабильность); 3. Дополнительная инфа улучшает качество оценок; 4. При прочих равных более предпочтительны эксперты, дающие малую дисперсию на тестовых испытаниях.

КОМПЕТЕНТНОСТЬ ЭКСПЕРТОВ. Задачи делятся: высокой информационной емкости – в содержательном контексте (важно качество каждого эксперта (космос)); низкой инф-ной емкости (все оценки одинаковы (мнения экспертов равноценны, напр., косметика), можно решать как в мат.стате).

ЧИСЛО ЭКСПЕРТОВ 1) неравенство Чебышева n_min>=σ²/(1-p)*ε², σ - тестовое значение дисперсии оценок экспертов, р- вероятность того что средняя оценка ≥ истина, ε – предельная (априори) ошибка экспертов. !!!добавить коэффициенты, а надо ли

Кач-во экспертного оценивания зависит от: -кач-ва экспертов (априорная оценка); -апостериорное – как судить о кач-ве экспертизы, если она уже сделана (но событие еще не наступило). Стандартные критерии оценки качества: полезность, достоверность, издержки на составление прогноза не претерпевают изменений, а НАДЕЖНОСТЬ и ИНФОРМАТИВНОСТЬ (полнота отчета, зависит от шкалы, лучшая - интервальная) зависят от выбранных методов. Интегральные измерители априорной надежности экспертных прогнозов – характеритики групповой устойчивости и согласованности. УСТОЙЧИВОСТЬ – независимость итоговой оценки от кач-го или кол-го состава членов группы (вероятность неизменения итогового результата от величины группы экспертов). СОГЛАСОВАННОСТЬ – степень качественного совпадения мнений экспертов. Группы характеристик согласованности: -коэф-ты согласия (конкордации); -меры расстояния; -коэф-ты ассоциативности; вероятностные коэф-ты сходства (энтропийный коэф-т согласия). Коэф-ты согласия зависят от шкал: 1. Интервальная (корреляции, ковариации); 2. Порядковая (Кендалл и Спирмэн бывают: парные (конкордации), множественные (дисперсионный к-т конкордации (множественный к-т конкордации Кендалла)); 3. Номинальная (к-т ассоциации). ОБЩИЙ СОСТАВ ЗАДАЧ оценки надежности:-обработка входящей инфы; -оценка согласованности экспертов (как по отдельному фактору, так и по набору в целом), выделение экспертов со схожими оценками (экспертные ядра); -при большом расхождении в мнениях оценка проблем ( а) выявить принципы; б) решение о дальнейшей стратегии экспертизы), дополнительное уточнение состава группы экспертов.