
- •Математические основы моделирования. Численные методы.
- •1. Классификация экономико-математических моделей.
- •3. По способу использования:
- •3. Математические схемы моделирования систем: стохастические схемы формализованного описания систем.
- •4. Численные методы Монте-Карло: розыгрыш дискретной случайной величины; розыгрыш непрерывной случайной величины.
- •Для чтения (если очень углубляться). §1. Розыгрыш значений дискретной случайной величины.
- •§2. Получение значений непрерывных случайных величин.
- •Раздел 2. Экономико-математическое моделирование.
- •2.1 Моделирование микроэкономических процессов и систем.
- •Направления применения экономико-математических методов в планировании и управлении производством.
- •Эвристические методы решения задач производственного планирования.
- •Задача объемного планирования.
- •Объемно-календарное планирование.
- •Календарное планирование.
- •Оперативное планирование.
- •7. Ресурсные методы оптимизации в сетевом планировании и управлении.
- •8. Модели объемного и объемно - календарного планирования.
- •1Этап. Получение первого прогнозного значения объемной характеристики
- •9. Модели оперативного планирования и построения графиков производства.
- •12. Расчет временных параметров сети и оптимизация сети по времени.
- •2.2 Моделирование макроэкономических процессов и систем.
- •13. Моделирование валового внутреннего продукта с помощью производственных функций: их типы, характеристики и методика построения.
- •14. Постановка задачи оптимизации выпуска в долгосрочном периоде (изокванта, изокоста, предельный продукт).
- •15. Модели межотраслевого баланса (моб): понятие, методы расчета и свойства прямых, косвенных и полных затрат; области применения.
- •2 Схемы анализа выпуска:
- •16. Постановка и обоснование задачи оптимального (стационарного) технологического и экономического роста в модели расширяющейся экономики фон. Неймана.
- •21. Синтез оптимальной траектории модели Харрода-Домара с переменной нормой накопления.
- •22. Синтез оптимальной траектории Солоу с переменной нормой накопления.
- •23. Принцип оптимальности Беллмана и принцип оптимальности Понтрягина.
- •24. Системный анализ и моделирование социально-экокономических процессов.
- •25. Системный подход к организации и ее особенности как сложной кибернетической системы.
- •2 6. Исследование систем и процессов на основе имитационного моделирования.
- •27. Парадигмы современного имитационного моделирования.
- •28. Метод системной динамики и его программная реализация в виде системы Any Logic. Имитационные модели рынка в системе Any Logic.
- •29. Дискретно-событийный подход имитационного моделирования.
- •30. Концепция баз данных: определение бд, принципы организации.
- •32. Проектирование бд: жизненный цикл бд, схема, подходы к проектированию.
- •Анализ и проектирование.
- •Реализация и функционирование.
- •33. Распределенная база данных: определение, стратегии распределения. Архитектура систем управления распределенными базами данных.
- •34. Концепция баз знаний: понятие, общая характеристика моделей представления знаний.
- •35. Тенденции развития корпоративных информационных систем.
- •36. Главные функции и возможности модулей финансовой подсистемы Oracle e-Business Suite.
- •37. Настройка и функционал модулей финансовой подсистемы Oracle е-Business Suite (Кредиторы, Дебиторы, Основные средства, Главная книга).
- •38. Настройка и функционал Книги материального учета - Oracle InventorV.
- •39. Интеграция программных модулей финансовой подсистемы Oracle e-Business Suite.
- •40. Теория поведения потребителя.
- •41. Теория издержек.
- •42. Особенности применения моделей рынка: совершенной конкуренции, монополии.
- •43. Характеристики отраслевой экономической среды с позиций модели конкуренции в отрасли.
- •44. Теория фирмы. Основные формы поведения фирмы на товарном рынке.
- •45. Анализ финансовой обеспеченности инвестиционных решений.
- •46. Прогнозирование финансово-экономической деятельности хозяйствующих субъектов.
- •47. Назначение ндс и методика его расчета.
- •48. Записать корреспонденцию счетов по следующим хозяйственным операциям.
- •49. Примеры атипичного применения бухгалтерского учета.
- •50. Как и зачем используется балансовый метод в бухгалтерском учете.
- •51. Вариантность при организации применения бухгалтерского учета.
- •52. Экономико-математическая постановка оптимизации бухучета.
- •Раздел 5. Методы социально-экономического прогнозирования
- •53. Выявление и прогноз динамики временных рядов на основе методологии Бокса-Дженкинса.
- •54. Предикативные факторные регрессионные модели, выявление и коррекция ошибок спецификации
- •1) Коэф. Корреляции Спирмэна (парный для стандартизированной ранжировки):
- •60. Адаптивное прогнозирование: принципы, методы, оценка качества механизмов и прогнозов.
- •61. Специфика моделирования многомерных динамических рядов. Тестирование на коинтегрированность.
- •Раздел 6. Теория риска и моделирование рисковых ситуаций
- •Формализация общей постановки задачи принятия решений, логические элементы ее составляющие и основные типы математических моделей процесса выбора решений.
- •Многокритериальный подход к принятию решений в условиях определенности с учетом наличия информации о системе предпочтений лица принимающего решение.
- •66. Понятие риска, классификация риска и основные методы оценки риска.
- •68. Модели многокритериального выбора в условиях нечеткой постановки задачи принятия решений.
- •71. Методология нового институционализма, его возможности и пределы.
- •72. Институты и правила в институциональной экономической теории..
- •73. Трансакционные издержки и институты.
- •74. Основные понятия и методы начисления процентов и дисконтирования процентов
- •Методы анализа потоков платежей
- •Показатели доходности и оценки курсов ценных бумаг
- •Методы кредитных расчетов
- •Методы оценки инвестиционных проектов
- •Задача об оптимальном портфеле ценных бумаг. Модели Марковица и Тобина
- •Понятие рыночного портфеля ценных бумаг. Основное уравнение равновесного рынка
- •Общий, рыночный и диверсифицируемый риски финансовых активов.
Для чтения (если очень углубляться). §1. Розыгрыш значений дискретной случайной величины.
Пусть
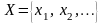 - множество значений дискретной случайной
величины
- множество значений дискретной случайной
величины
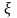 ,
,
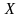 - конечное или счетное множество,
- конечное или счетное множество,
 (3)
(3)
 Стандартный
метод розыгрыша
заключается в следующем. Отметим на
интервале
Стандартный
метод розыгрыша
заключается в следующем. Отметим на
интервале
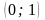 точки
точки
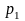 ,
,
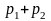 ,
,
 ,
,
 ,
.
Получив значение
,
.
Получив значение
 ,
смотрим: если
,
смотрим: если
 ,
то полагаем
,
то полагаем
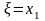 если
если
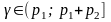 ,
то полагаем
,
то полагаем
 ,
и т.д., т.е. если
,
и т.д., т.е. если
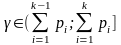 ,
то
,
то
 (
(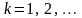 ) (4)
) (4)
Алгоритм (4) дает значение распределения (3). Действительно, т.к. , то
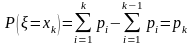 .
.
На рис. 1 приведена блок-схема розыгрыша одного значения случайной величины с распределением (3).
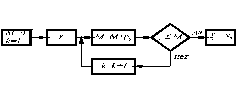 Рис.1.
Рис.1.
Некоторое
неудобство стандартного метода
заключается в необходимости хранить в
памяти все
и
 .
В случае целочисленных значений
.
В случае целочисленных значений
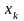 (например,
(например,
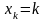 )
предложенный выше алгоритм можно
усовершенствовать. Допустим, что нам
известна последовательность
)
предложенный выше алгоритм можно
усовершенствовать. Допустим, что нам
известна последовательность
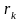 ,
таких, что
,
таких, что
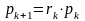 .
.
Например,
для биномиального распределения с
параметрами
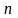 и
и
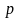 (пишем
(пишем
 )
)
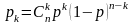 ,
следовательно,
,
следовательно,

Для
распределения Пуассона с параметром
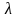 (пишем
(пишем
 )
)
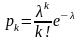 (
(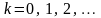 ),
следовательно,
),
следовательно,
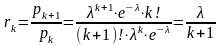 (
).
(
).
В случае
геометрического распределения,
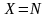 ,
,
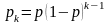 ,
поэтому
,
поэтому
 (
).
(
).
В этом
случае нужно запомнить
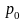 и формулу для
.
Блок-схема алгоритма розыгрыша одного
значения приведена на рис. 2.
и формулу для
.
Блок-схема алгоритма розыгрыша одного
значения приведена на рис. 2.
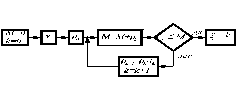
Рис. 2.
§2. Получение значений непрерывных случайных величин.
Стандартный
метод розыгрыша.
Пусть требуется разыграть случайную
величину
,
имеющую функцию распределения
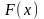 ,
и
.
Функция распределения
,
и
.
Функция распределения
 случайной величины
случайной величины
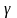 имеет вид
имеет вид

Покажем, что решение уравнения
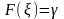 (6)
(6)
- требуемое значение случайной величины .
 .
.
Таким
образом, для получения значений случайной
величины
надо для каждого значения
решить уравнение (6). Если
 строго возрастает, то получаем моделирующую
формулу
строго возрастает, то получаем моделирующую
формулу
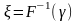
(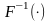 -
функция, обратная к
).
-
функция, обратная к
).
В качестве примеров получим моделирующие формулы для некоторых стандартных распределений.
1.
 :
:
 при
при
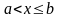 ,
уравнение (6) принимает вид
,
уравнение (6) принимает вид
 ,
следовательно получаем моделирующую
формулу
,
следовательно получаем моделирующую
формулу
 . (7)
. (7)
2.
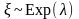 (
имеет показательное распределение с
параметром
);
(
имеет показательное распределение с
параметром
);
 при
при
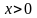 .
Следовательно,
.
Следовательно,
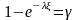 ,
,
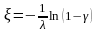 .
Но так как
.
Но так как
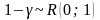 ,
то окончательно получаем моделирующую
формулу
,
то окончательно получаем моделирующую
формулу
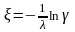 (8)
(8)
3.
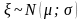 (
имеет нормальное распределение с
параметрами
(
имеет нормальное распределение с
параметрами
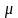 и
и
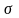 ).
).
 ;
уравнение (6) принимает вид
;
уравнение (6) принимает вид
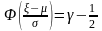 .
.
Таким образом, надо решить уравнение
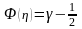 (9)
(9)
и затем
положить
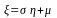 .
Так как уравнение (9) (с помощью таблиц)
можно решить лишь приближенно с большой
погрешностью, то для моделирования
нормального распределения обычно
поступают иначе.
.
Так как уравнение (9) (с помощью таблиц)
можно решить лишь приближенно с большой
погрешностью, то для моделирования
нормального распределения обычно
поступают иначе.
Пусть
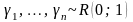 ,
,
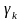 независимы. Так как
независимы. Так как
 ,
,
 ,
то
,
то
 ,
,
 .
Согласно центральной предельной теореме
сумма
.
Согласно центральной предельной теореме
сумма
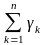 асимптотически нормальна, т.е.
асимптотически нормальна, т.е.
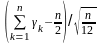 по распределению сходится к
по распределению сходится к
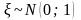 .
Поэтому полагают
.
Поэтому полагают
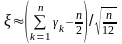 .
Для удобства расчетов берут
.
Для удобства расчетов берут
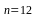 или
или
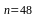 (в случае, если нужна большая точность),
поэтому
(в случае, если нужна большая точность),
поэтому
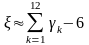
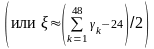 . (10)
. (10)
Для
моделирования
следует положить 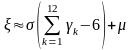
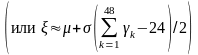
Раздел 2. Экономико-математическое моделирование.
2.1 Моделирование микроэкономических процессов и систем.
Направления применения экономико-математических методов в планировании и управлении производством.
Важнейшие экономико-математические методы, применяющиеся для решения преимущественно плановых и других экономических задач. В таблице изображено, с помощью каких методов могут решаться присущие каждому из направлений задачи (Прогнозирование, объемное планирование, календарное планирование, планирование перевозок, балансовые расчеты, размещения производства, статистика, управление запасами, раскрои, составление, массовое обслуживание и конфликтные ситуации).
Линейное программ-ие – линейное преобразование переменных в системах линейных ур-ий. Сюда следует отнести: симплекс-метод, распределительный метод, метод разрешающих множителей и т.д.
Дискретное программ-ие представлено двумя классами методов: локализационный и комбинаторный. К локал. относятся методы линейного целочисленного программ-ия. К комбин. – метод ветвей и границ, испол. для построения графиков производства и т.п.
Матем. статистика испол. для корреляционного, регрессионного и дисперсионного анализов экон-их явлений и процессов. Корреляционный анализ применяется для установления тесноты связи между двумя и более стохастически независимыми явлениями или процессами. Регрессионный анализ устанавливает зависимость СВ от неслучайного аргумента. Д. а. испол. для установления зависимости результатов наблюдений от одного или нескольких факторов в целях выявления важнейших. Методы математической статистики используются также для прогностических экономических расчетов.
Динамическое программ-ие применяется для планирования и анализа экономических процессов во времени. Динамическое программ-ие представляется в виде многошагового вычислительного процесса с последовательной оптим. целевой функции. Сюда следует отнести и имитационное модел-ие.
Теория игр представляется рядом методов, испол. для определения стратегии поведения конфликтующих сторон. Методы можно разделить на два класса – точные и приближенные (итеративные). Условно точная игра может реализоваться на основе линейного программ-ия. Реализация игры основана на аналитическом осмыслении стратегии на каждом шаге с целью совершенств.поведения на последующих шагах.
Теория массового обслуживания включает большой класс экономических задач, где на основе теории вероятностей оцениваются мощность или количество. При этом многие задачи управления запасами формализуются как задачи м. о. и алгоритмически представляются как эвристические модели.
Параметрическое программ-ие явл. разновидностью линейного программ-ия, где, коэфф-ты при переменных линейного функционала, или коэфф-ты при переменных системы линейных ур-ий, или те и другие коэфф-ты зависят от некоторого параметра. К этому направлению может быть отнесен динамический матричный метод решения материальных балансов.
Стохастическое программ-ие делится на статистическое и динамическое. В стат. задачах исследуемые параметры являются СВ на определенном этапе. В динам.задачах имеют дело со случайными последовательностями. Динам.задачи являются предметом так называемого Марковского программ-ия.
Нелинейное программ-ие относится к наименее изученному, применительно к эконом-им явл. и процессам, матем. направлению. Большинство изученных численных методов нелинейного программ-ия посвящено решению задач квадратичного программ-ия на основе симплекс-метода.
Теория графов – направление матем., где на основе определенной символики представляется формальное описание взаимосвязанности и взаимообусловленности множества работ, ресурсов, затрат и т.п. Наибольшее практическое применение получил так называемый сетевой график (сетевой метод). На основе этой формализации с помощью эвристических или матем. методов осуществл. исследование выделенного множества на предмет установления оптим. времени производства работ, оптим. распредел. запасов и т.п. Одним из методов формализ-ого исслед-ия явл. эвристические алгоритмы систем ПЕРТ (сеть общего вида) и ДЕРЕВО, а также линейное и нелинейное программ-ие на базе симплекс-метода.
