4. Численные методы Монте-Карло: розыгрыш дискретной случайной величины; розыгрыш непрерывной случайной величины.
МСИ (метод Монте-Карло) применяют при моделировании случайных процессов, которые невозможно или трудно описать аналитически. Алгоритм метода статистических испытаний: - разыгрывается случайное явление с помощью некоторой процедуры, которая даёт случайный результат, - проводится большое количество реализаций, - полученные результаты обрабатываются методами теории вероятностей и рассчитываются оценки искомых величин. Метод статистических испытаний - это метод математического моделирования СВ, где каждый случайный фактор моделируется с помощью розыгрыша. Недостаток метода - необходимость проведения большого количества испытаний, чтобы получить результат с заданной точностью. При статистическом моделировании систем на ЭВМ имитация любых случайных процессов сводится к генерированию равномерно распределенных на [0;1] СЧ и их последующему функциональному преобразованию. Для генерации такой СВ используют генераторы СЧ. Выделяют 3 способа генерации: аппаратный (физический); табличный (файловый); алгоритмический (программный) - на рекуррентных формулах..
Розыгрыш дискретной СВ. Дискретная СВ ξ с распределением: построчно (x1 … xn); (p1…pn),(1), где pi=P{ξ=xi }. Для того чтобы вычислить значения этой величины, разделим интервал 0≤η≤1 на интервалы Δi такие, что длина |Δi|=pi. Тогда СВ. ξ, определенная формулой ξ =xi , когда ηϵΔi,(2) имеет заданное распределение вероятностей (1).
Для практической реализации формулы (2) удобно в накопителе расположить подряд значения x1,…,xn и p, p1+p2, p1+p2+p3,…,1. Для того, чтобы вычислить очередное значение ξ, находим очередное η. Затем сравниваем η с p1. Если η<p1, то ξ=x1; если η≥p1, то сравниваем η с p1+p2. Если η<p1+p2, то ξ=x2; если η≥p1+p2, то сравниваем η с p1+p2+p3, и т.д.
Розыгрыш непрерывных СВ на основе поиска обратной функции распределения. Для формирования возможных значений СВ с заданным законом распределения исходным материалом служат базовые последовательности СЧ {xi}, имеющие равномерное распределение в интервале(0;1).
Пример.
Непрерывная СВ ξ называется равномерно
распределенной в интервале (a,b),
если она определена в интервале и ее
функция плотности имеет вид p(x):
система{1/(b-a),
xϵ[a,b];
0, xϵ(-∞,a)ᴗ(b,+∞)}.
Непрерывная СВ η
задается интегральной функцией
распределения Fη(y)=
,
где fη(y)
- плотность распределения.
Для получения непрерывной СВ с заданным законом распределения можно воспользоваться методом обратной функции. Метод обратной функции состоит в следующем. Если ξ - равномерно распределенная на интервале (0;1) СВ., то искомая СВ. η получается с помощью преобразования
η=F-1η(ξ),где
F-1η
- функция, обратная Fη.
Другими словами, взаимно однозначная
монотонная функция η=F-1η(ξ),
полученная решением относительно η
уравнения Fη(y)=ξ,
преобразует равномерно распределенную
на интервале (0;1) величину ξ в η
с требуемой плотностью fη(y).
Если СВ. η
имеет плотность распределения fη(y),
то распределение СВ ξ=
является
равномерным в интервале (0;1). Поэтому
чтобы получить число, принадлежащее
последовательности СЧ {yi},
имеющих функцию плотности fη(y),
необходимо разрешить относительно
уравнение
.
Пример.
Получим СЧ yi
с показательным законом распределения
fη(y)=λe-λy.Пусть
xi
– СЧ, имеющее равномерное распределение
(0;1). Тогда
.
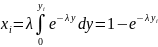Разрешив это уравнение относительно
yi,
получим yi=
-ln(1-xi)/λ.
Если СВ ξ имеет равномерное распределение
в интервале (0;1), то и СВ 1- ξ также имеет
равномерное распределение в интервале
(0;1). Поэтому можно записать yi=-lnxi/λ.
Для определения площади под графиком функции можно использовать следующий стохастический алгоритм:
ограничим функцию прямоугольником (n-мерным параллелепипедом в случае многих измерений), площадь которого Spar можно легко вычислить;
«набросаем» в этот прямоугольник (параллелепипед) некоторое количество точек (N штук), координаты которых будем выбирать случайным образом;
определим число точек (K штук), которые попадут под график функции;
площадь области, ограниченной функцией и осями координат, S даётся выражением
Для малого числа измерений интегрируемой функции производительность Монте-Карло интегрирования гораздо ниже, чем производительность детерминированных методов. Тем не менее, в некоторых случаях, когда функция задана неявно, а необходимо определить область, заданную в виде сложных неравенств, стохастический метод может оказаться более предпочтительным