14. Постановка задачи оптимизации выпуска в долгосрочном периоде (изокванта, изокоста, предельный продукт).

Длительный период – промежуток времени (протяженный), в течение кот-го фирма могла изменить все используемые факторы производства (=>все факторы производства переменные). Также выделяют понятие очень длительный период – меняются не только факторы, но и сама технология (в теории фирмы интерпретируется как изменение ПФ).

В микроэк-их ПФ K и L обозначают капитал и труд в рамках отдельной фирмы, Y – выпуск продукции в натуральном выражении.

И зокванта (линия постоянного выпуска Y=Y₀,) множество точек на координатной плоскости с осями K и L таких, что выпуск одинаковый F(K;L)= Y₀.

Св-ва изокванты: - Изокванты различных уровней не пересекаются.- Изокванты, расположенные дальше от нуля, соответствуют большему объему выпуска. - Изокванта – это убывающая выпуклая вниз функция зависимости K(L).

И зокоста (линия постоянных издержек уровня С=С₀) – показывает набор комбинаций экономических ресурсов, которые фирма может приобрести с учетом рыночных цен на ресурсы при полном использовании своего бюджета:

Текущие затраты:

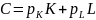
– цена использования капитала (расходы на содержание и эксплуатацию ед-цы осн-го средства; – цена ед-цы труда (зарплата 1го работника).

Предприятие обладает ограниченными денежными средствами I (эти средства она тратит для покрытия текущих затрат): C=I

Задача оптимизации выпуска:(в постановке задачи ≤, но решается как равенство)

Y = F(K;L)→max

Задача имеет смысл только в длительном периоде (т.к. фирма имеет возможность изменить и труд и капитал).

Функция Лагранжа:

Необходимо решить систему:

: отношение предельной эффективности ресурса ( к цене ресурса – предельный продукт данного ресурса.

Т.о., в ситуации максимального выпуска продукции предельные продукты всех ресурсов равны друг другу и равны множителю Лагранжа (это утверждение в т. фирмы аналогично 2ому закону Госсена в т. потребления). Множитель Лагранжа в т. фирмы как и в т. потребления означает предельная полезность денег. Он показывает насколько возрастет выпуск продукции если объем имеющихся денежных средств I увеличится на малую единицу.

K ^* и L^* - найденные оптимальные знания. Им соответствует опт-ое зн-ие выпуска Y^* (Y^* отвечает некоторая изокванта) и (получаем уравнение изокосты: , K и L - переменные)

Т.о. графически точка оптимума в задаче на максимизацию выпуска продукции фирмы есть точка касания изокостой (прямая) изокванты (кривая).

15. Модели межотраслевого баланса (моб): понятие, методы расчета и свойства прямых, косвенных и полных затрат; области применения.

Межотраслевой баланс (МОБ, метод «затраты-выпуск») — экономико-математическая балансовая модель, характеризующая межотраслевые производственные взаимосвязи в экономике страны. Характеризует связи между выпуском продукции в одной отрасли и затратами, расходованием продукции всех участвующих отраслей, необходимым для обеспечения этого выпуска. Межотраслевой баланс составляется в денежной и натуральной формах.

Межотраслевой баланс представлен в виде системы линейных уравнений. Межотраслевой баланс (МОБ) представляет собой таблицу, в которой отражен процесс формирования и использования совокупного общественного продукта в отраслевом разрезе. Таблица показывает структуру затрат на производство каждого продукта и структуру его распределения в экономике. По столбцам отражается стоимостный состав валового выпуска отраслей экономики по элементам промежуточного потребления и добавленной стоимости. По строкам отражаются направления использования ресурсов каждой отрасли.

К основным задачам межотраслевого баланса относятся:

• характеристика воспроизводственных процессов в экономике по материально-вещественному составу в детальном отраслевом разрезе;

• отражение процесса производства и распределения продукции, созданной в сфере материального производства и услуг;

• детализация счетов товаров и услуг, производства, образования доходов и операций с капиталом на уровне отраслевых групп продуктов и услуг;

• выявление роли факторов производства и их эффективное использование для экономического развития.

Структура межотраслевого баланса производства и распределения продукции приведена в табл. 1. Каждая отрасль фигурирует в балансе и как производящая и как потребляющая.

Таблица 3.1 - Общая структура межотраслевого баланса

1. Первый квадрант – это таблица межотраслевых связей. Величина x_ij равна объему продукции i-й отрасли, использованной в качестве материальных затрат j-й отраслью в ее производстве. Сумма элементов i-й строки представляет промежуточный продукт i-й отрасли, который поступает в дальнейшее производственное использование. Сумма элементов j-го столбца представляет материальные издержки j-й отрасли.

2. Второй квадрант содержит конечную продукцию отраслей. Под конечной продукцией понимается часть продукции, выходящая за пределы текущего производственного потребления. Она используется на личное и общественное потребление, пополнение запасов, накопление, возмещение потерь, экспорт за минусом импорта. Второй квадрант характеризует отраслевую структуру национального дохода.

3. Третий квадрант характеризует национальный доход со стороны его стоимостного состава. Сумма чистого дохода (прибыли) отраслей и оплаты труда называется чистой продукцией или добавленной стоимостью. Сумма амортизации и добавленной стоимости обозначается Z_j и называется условно-чистой продукцией Z_j = c_j + v_j + m_j, j=1,2,…,n.

4. Четвертый квадрант находится на пересечении столбца конечной продукции и строк третьего квадранта. При его подробном раскрытии он отражает конечное распределение национального дохода на доходы населения, предприятий и государства и показывается направления его использования на потребление и накопление.

Валовая продукция состоит из промежуточного и конечного продукта. Суммируя показатели таблицы по строкам, получим (2). С другой стороны, валовая продукция включает материальные издержки и условно-чистую продукцию, поэтому, суммируя столбцы таблицы МОБ, получим (3). Сложим n уравнений системы (2): и системы 3: . Первые части последних двух равенств одинаковы, значит, одинаковы и левые, отсюда , т.е. суммарный конечный продукт народного хозяйства равен суммарной условно-чистой продукции.

Анализ таблиц размерности 41х41 для 1919 и 1929г. Показал, что хотя межотраслевые поставки x_ij изменяются от года к году, относительные величины (5) меняются незначительно, являются устойчивыми. Коэффициенты a_ij называются коэффициентами прямых материальных затрат. Величина a_ij показывает, какое количество продукции i-й отрасли необходимо, чтобы i-я отрасль провела единицу валовой продукции.

Устойчивость коэффициентов прямых материальных затрат дает возможность, составит отчетный баланс о работе экономики за какой-либо год и рассчитав коэффициенты a_ij, использовать их для целей планирования или для прогнозирования развития экономики в будущем.

Коэффициенты a_ij определяются сложившейся технологией производства, поэтому их называют технологическими коэффициентами. Они образуют технологическую матрицу А размерностью n*n.

С использованием коэффициентов прямых материальных затрат из (5) можно выразить величины межотраслевых поставок и получим, что AX+Y=X (7). Данная система называется экономико-математической моделью межотраслевого баланса или моделью «затраты-выпуск» (моделью Леонтьева).

Используя модель «затраты-выпуск» можно решать две основные задачи:

1. Пусть известна валовая продукция отраслей, т.е. вектор Х и требуется найти конечную продукцию, т.е. вектор Y. Конечная продукция будет равна Y=X-AX.

2. Задана конечная продукция отраслей, т.е. вектор Y, требуется найти валовую продукцию X, выпуск которой обеспечит заданный уровень конечной продукции. Данная задача возникает при планировании работы отраслей для достижения необходимых целей, выраженных в объемах конечной продукции. Для решения этой задачи перепишем систему в виде X-AX=Y или (E-A)X=Y. Откуда находим: X=(E-A)^-1Y=BY. Элементы матрицы В называются коэффициентами полных материальных затрат, а сама матрица – матрицей полных материальных затрат.

В зависимости от цели и объекта исследования межотраслевые балансы классифицируются по следующим признакам:

• единицы измерения (натуральные, натурально-стоимостные, ценностные);

• объект анализа (народнохозяйственные, районные, межрайонные, внутриотраслевые межпродуктовые);

• период анализа (статические, динамические);

• цель исследования (отчётные, плановые).