Вопрос 5.3. Системы линейных алгебраических уравнений.

Определение 5.2. Системой линейных алгебраических уравнений называется система вида

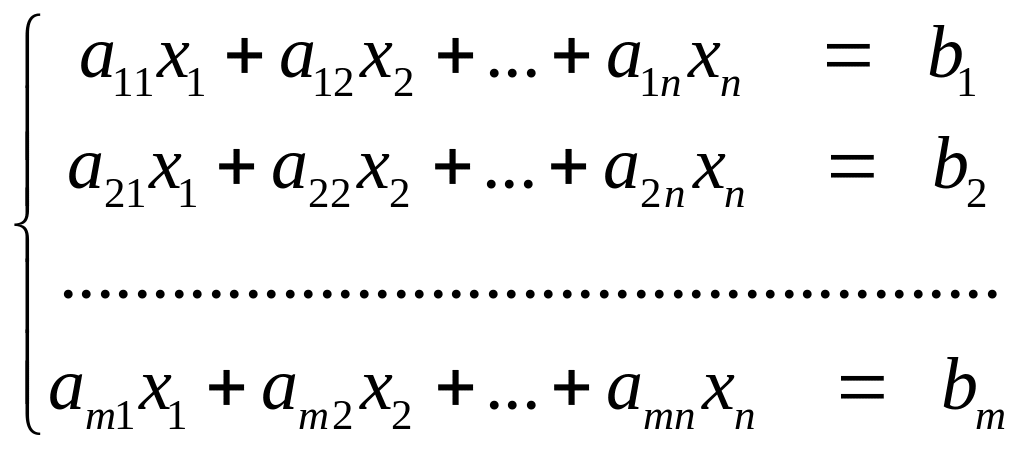
Числа называются коэффициентами системы уравнений. Числа называются правыми частями системы уравнения. Величины называются неизвестными, их число может не равняться числу уравнений.

Определение 5.3. Решением системы называются любые числа , которые при подстановке в систему уравнений обращают каждое уравнение в верное числовое равенство.

Определение 5.4. Матрицей коэффициентов системы линейных алгебраических уравнений называется матрица

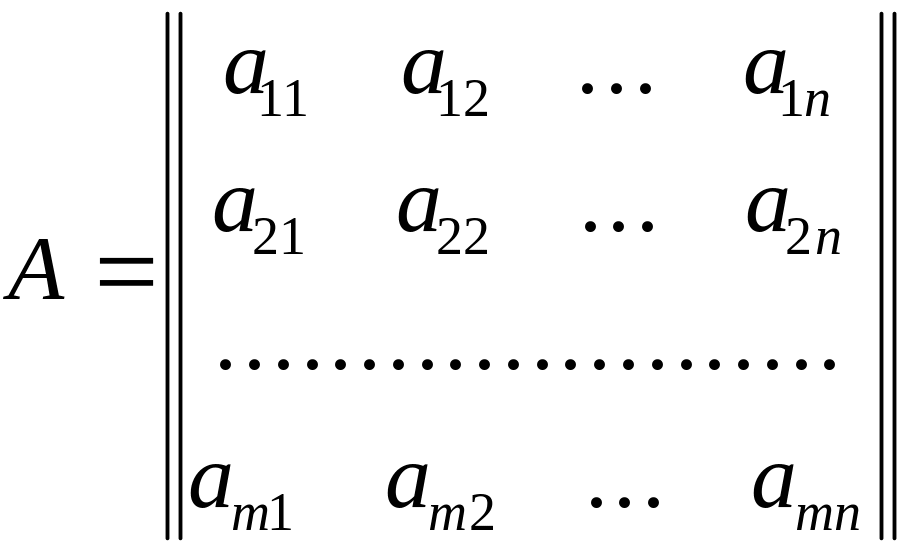
Определение 5.5. Столбцом неизвестных и столбцом правых частей называются соответственно следующие матрицы

Используя матричное исчисление, систему линейных уравнений можно записать в виде одного матричного уравнения

.

Определение 5.6. Система линейных уравнений называется однородной, если все ее правые части равны нулю и неоднородной в противном случае.

Определение 5.7. Система линейных уравнений называется совместной, если она имеет хотя бы одно решение.

Определение 5.8. Система линейных уравнений называется несовместной, если она не имеет решений.

Определение 5.9. Совместная система линейных уравнений называется определенной, если она имеет ровно одно решение.

Определение 5.10. Совместная система линейных уравнений называется неопределенной, если она имеет несколько решений.

Вопрос 5.4. Матричный способ решения систем линейных алгебраических уравнений.

Выше отмечалось, что систему линейных уравнений можно записать в виде одного матричного уравнения .

Пусть A квадратная матрица и ее определитель отличен от нуля. Тогда существует обратная к A матрица. Умножим матричное уравнение на обратную матрицу слева

или

Таким образом, чтобы получить решение системы матричным способом, нужно, обратную к матрице коэффициентов, матрицу умножить слева на столбец правых частей.

Теперь можно сделать такой вывод: система линейных уравнений, матрица коэффициентов которой имеет отличный от нуля определитель, имеет ровно одно решение.

Пример 5.3. Решить систему уравнений

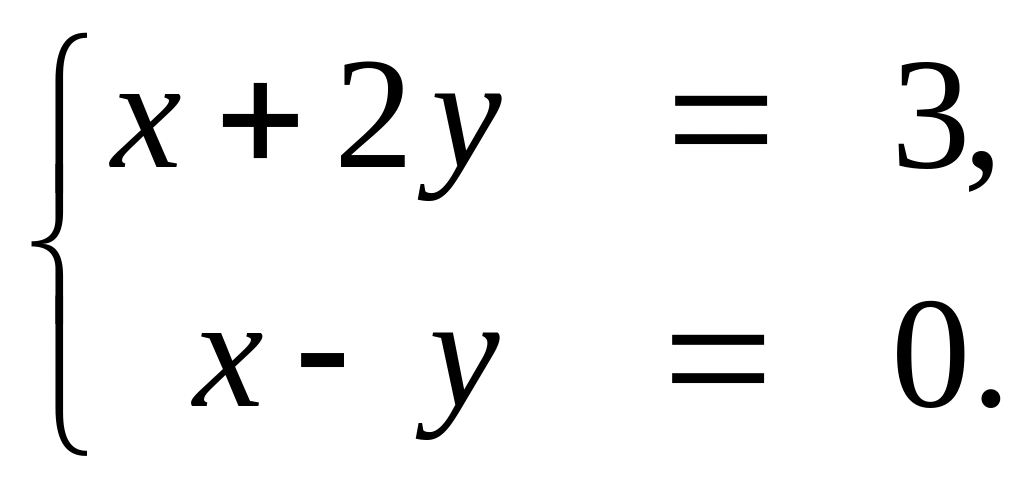
Составим матрицы

.

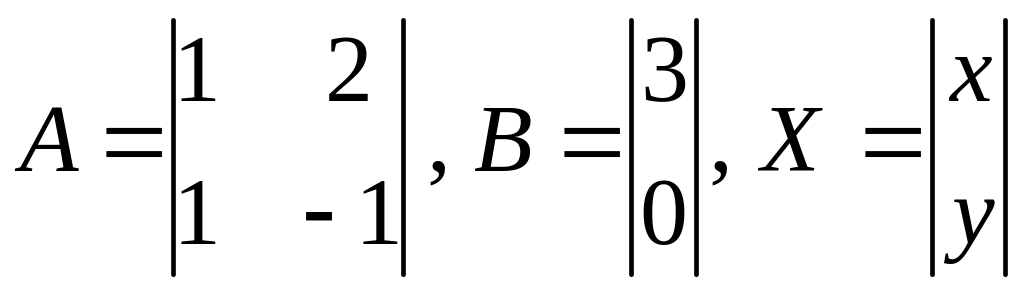Вычислим определитель , затем обратную матрицу

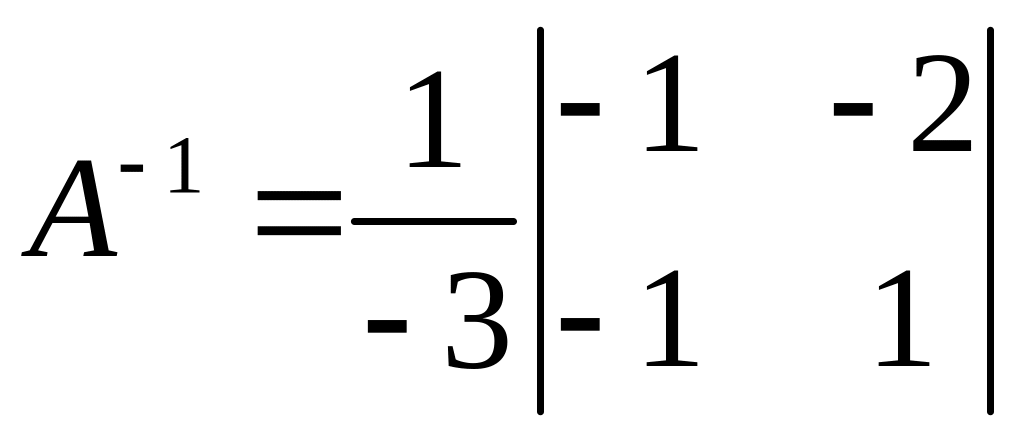
Тогда получим

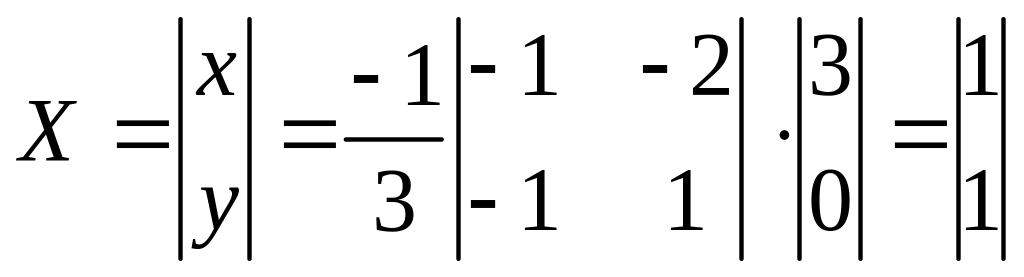или x=1, y=1

Конец примера.

ЛЕКЦИЯ № 6. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.

Вопрос 6.1. Правило Крамера.

Пусть дана система линейных алгебраических уравнений, матрица коэффициентов которой является квадратной и несобственной

.

Тогда, как известно из предыдущей лекции, решение системы дается матричной формулой

.

Будем для простоты рассматривать систему с тремя неизвестными. Тогда

.

Перемножая матрицы, получим

.

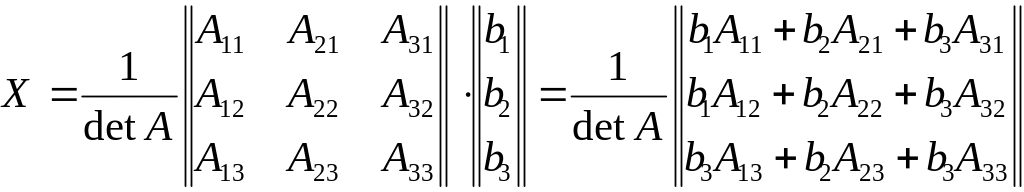Обозначим главный определитель системы через . Так как по теореме Лапласа

,

,

.

Отсюда 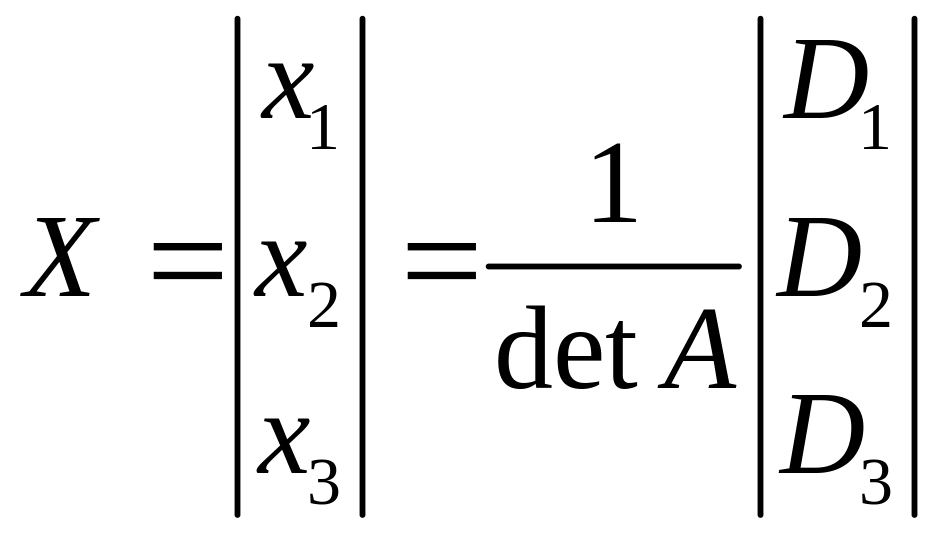или .

Пример 6.1. Решить по правилу Крамера систему уравнений

Вычислим главный определитель системы

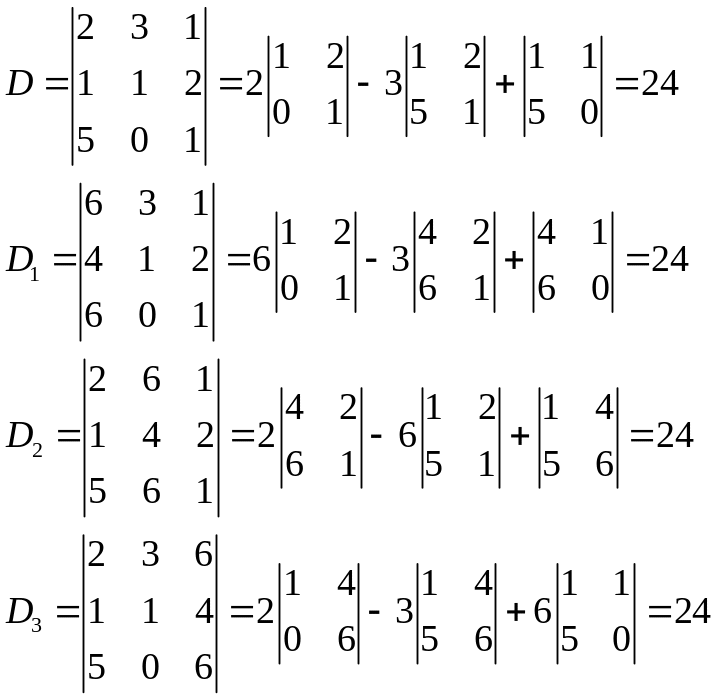
Отсюда получаем

.

Конец примера.