Государственное образовательное учреждение

Высшего профессионального образования

Кубанский государственный технологический университет

(КубГТУ)

Кафедра общей математики

И.В. Терещенко И.В., А.В. Братчиков

М А Т Е М А Т И К А

Часть 4

Конспект лекций для студентов заочной формы обучения факультета Нефти, Газа и Энергетики всех специальностей

Краснодар

2006

УДК:

Математика. Часть 4:

Конспект лекций/И.В. Терещенко, А.В. Братчиков; Кубан. гос. технол. ун-т.-Краснодар : Издательство КубГТУ, 2006.-96с.

ISBN………..

Рассмотрены основные вопросы курса математики по разделам «Теория функций комплексного переменного», «Операционное исчисление», «Уравнения математической физики», «Теория вероятности и математическая статистика», изучаемые в четвертом семестре.

Предназначено для студентов заочной формы обучения факультета Нефти, Газа и Энергетики всех специальностей.

Ил. 10. Библиог.: 21 назв.

Рецензенты: канд. тех. наук, Доцент Л.М. Данович;

д-р тех. наук, профессор Г.Т. Вартумян

© Кубанский государственный технологический университет, 2006

С О Д Е Р Ж А Н И Е

ЛЕКЦИЯ № 1. Функции комплексной переменной. ……………..…6

Вопрос 1.1. Основные определения и понятия.

Вопрос 1.2. Однозначные и многозначные функции. Ветви многозначных функций.

Вопрос 1.3. Предел и непрерывность.

Вопрос 1.4. Производная. Условия Коши-Римана.

ЛЕКЦИЯ № 2. Функции комплексной переменной. .……...………12

Вопрос 2.1. Гармонические и аналитические функции.

Вопрос 2.2. Геометрический смысл модуля и аргумента производной аналитической функции.

Вопрос 2.3. Конформные отображения.

Вопрос 2.4. Интегрирование по комплексной переменной. Регулярность первообразной.

ЛЕКЦИЯ № 3. Функции комплексной переменной.  16

Вопрос 3.1. Теорема Коши. Интегральная формула Коши.

Вопрос 3.2. Формулы для производных. Теорема Морера.

Вопрос 3.3. Ряды Тейлора и Лорана.

Вопрос 3.4. Ряды Лорана.

ЛЕКЦИЯ № 4. Функции комплексной переменной. ………….…...22

Вопрос 4.1. Изолированные особые точки, их классификация.

Вопрос 4.2. Вычеты, их вычисление.

Вопрос 4.3. Основная теорема о вычетах.

ЛЕКЦИЯ N 5. Операционное исчисление. ………………...26

Вопрос 5.1. Преобразование Лапласа, его свойства. Оригинал и изображение.

Вопрос 5.2. Основные теоремы операционного исчисления.

ЛЕКЦИЯ № 6. Операционное исчисление. ………………….30

Вопрос 6.1. Таблица оригиналов и изображений.

Вопрос 6.2. Основные теоремы операционного исчисления.

Вопрос 6.3. Свертка оригиналов. Теорема Бореля.

Вопрос 6.4. Способы восстановления оригинала по изображению и нахождения изображения от оригинала.

ЛЕКЦИЯ № 7. Операционное исчисление. ………………….30

Вопрос 7.1. Решение дифференциальных уравнений и систем операционным методом.

Вопрос 7.2. Интеграл Дюамеля.

Список литературы ………………………………………………………97

Лекция № 1. Функции комплексной переменной.

Вопрос 1.1. Основные определения и понятия.

Комплексные числа были рассмотрены в первой части конспекта лекций. Множество всех комплексных чисел будем обозначать символом C и каждое комплексное число z будем рассматривать геометрически как точку z плоскости. Эту плоскость будем называть комплексной плоскостью, и обозначать той же буквой C. Комплексная плоскость является метрическим пространством, в котором определена евклидова метрика, то есть расстояние между точками:

.

Наличие метрики позволяет рассмотреть теперь ряд геометрических и топологических понятий таких, как окрестность точки, внутренняя точка множества, предельная точка множества, открытое множество и т.д. Начнем с важнейших определений.

Определение 1.1.1. Открытым кругом радиуса r с центром в точке называется множество точек z комплексной области, удаленных от точки на расстояние меньшее r.

Конец определения.

Из определения следует, что точки открытого круга удовлетворяют неравенству . Открытый круг радиуса r с центром в точке будем обозначать символом .

Определение 1.1.2. ‑ окрестностью точки называется открытый круг радиуса с центром в точке .

Конец определения.

‑ окрестность точки будем обозначать символом . Геометрически она является кругом, у которого удалены точки, лежащие на расстоянии от точки .

Определение 1.1.3. Проколотым открытым кругом радиуса r с центром в точке называется множество точек комплексной области, удаленных от точки на расстояние меньшее r.

Конец определения.

Другими словами, точки проколотого открытого круга радиуса r с центром в точке удовлетворяют неравенству . Проколотый открытый круг радиуса r с центром в точке будем обозначать символом . Геометрически он является кругом, у которого удалены как точки, лежащие на расстоянии r от точки , так и сама точка .

Определение 1.1.4. Проколотой ‑ окрестностью точки называется проколотый открытый круг радиуса с центром в точке комплексной области.

Конец определения.

Из определения следует, что точки ‑ окрестности удовлетворяют неравенству . Проколотую ‑ окрестность точки будем обозначать символом .

Пусть D некоторое множество точек комплексной области.

Определение 1.1.5. Точка называется внутренней точкой множества D, если существует ‑ окрестность этой точки, целиком состоящая из точек множества D ( ).

Конец определения.

Определение 1.1.6. Точка комплексной плоскости C называется граничной точкой множества D, если в любой ‑ окрестности этой точки найдутся как точки принадлежащие множеству D, так и не принадлежащие этому множеству.

Конец определения.

Отметим особо, что сама граничная точка может быть точкой множества D, но может и не принадлежать этому множеству ( или ).

Определение 1.1.7. Точка комплексной плоскости C называется предельной точкой множества D, если в любой проколотой ‑ окрестности этой точки найдутся точки принадлежащие множеству D.

Конец определения.

Отметим, во-первых, что сама предельная точка может быть точкой множества D, но может и не принадлежать этому множеству ( или ), во-вторых, каждая проколотая окрестность точки может содержать кроме точек множества D точки, ему не принадлежащие.

Как следует из определения, любая внутренняя точка множества D является одновременно предельной точкой этого множества.

Определение 1.1.8. Точка называется изолированной точкой множества D, если существует проколотая ‑ окрестность этой точки, ни одна точка которой не принадлежит множеству D ( ).

Конец определения.

Из определения следует, что любая изолированная точка множества D является граничной точкой множества. Предельная точка множества D не может быть изолированной точкой множества.

Определение 1.1.9. Точка называется внешней точкой множества D (или внешней по отношению к множеству D), если существует ‑ окрестность этой точки, ни одна точка которой не принадлежит множеству D ( ).

Конец определения.

Замечание 1.1.1. По определению граничными точками множества D могут быть только предельные, не внутренние точки множества D, или изолированные точки множества D. В свою очередь, предельными точками множества D могут быть только внутренние точки этого множества D, либо граничные, но не изолированные точки множества D. Конечное множество точек не имеет предельных точек. Оно состоит целиком из изолированных точек.

Определение 1.1.10. Множество D называется открытым, если все его точки внутренние. Пустое множество комплексных точек по определению считается открытым множеством.

Конец определения.

Примером открытого множества D является открытый круг с центром в точке и радиусом r

.

Геометрически это утверждение очевидно. Однако в виду важности этого примера открытого множества приведем его доказательство.

Лемма 1.1.1. Открытый круг является открытым множеством.

Доказательство. Пусть произвольная точка открытого круга , удаленная от точки на расстояние . Рассмотрим  ‑ окрестность точки с радиусом . Покажем, что . Возьмем произвольную точку . Тогда

.

Следовательно, открытый круг . Поэтому произвольная точка является внутренней точкой и открытый круг является открытым множеством.

Конец доказательства.

‑ окрестность точки , как открытый круг радиуса , так же является открытым множеством. Все множество комплексных чисел C, очевидно, является открытым множеством. Тем же способом, каким была доказана лемма 1.1.1, не трудно доказать, что проколотый круг и проколотая ‑ окрестность , открытое кольцо являются примерами открытых множеств. Открытыми так же будут полуплоскости , , и , полосы и .

Определение 1.1.11. Всякое открытое множество V комплексных чисел, для которого точка является внутренней, называется окрестностью точки и обозначается .

Конец определения.

Таким образом, всякая окрестность точки должна содержать некоторую ‑ окрестность этой точки, то есть .

Определение 1.1.12. Всякое множество V комплексных чисел, которое содержит некоторую проколотую окрестность точки и не содержит саму точку , называется проколотой окрестностью точки и обозначается .

Конец определения.

Теорема 1.1.1. Система всех открытых множеств комплексной плоскости обладает следующими свойствами:

(1) и C являются открытыми множествами;

(2) объединение любого множества открытых множеств открыто;

(3) пересечение конечного множества открытых множеств открыто.

Доказательство. Утверждение (1) доказываемой теоремы очевидно. Перейдем теперь к утверждению (2).

Пусть z произвольная точка такая, что . Тогда точка z принадлежит одному из множеств семейства , например . Так как множество открыто, то точка z ‑ внутренняя точка множества . Тогда существует ‑ окрестность точки z такая, что . Поэтому . Следовательно, точка z внутренняя точка множества и это множество открыто.

Перейдем теперь к доказательству утверждения (3). Пусть z произвольная точка такая, что . Тогда для всех . Следовательно, z внутренняя точка множества . Поэтому существует открытый шар радиуса , принадлежащий . Пусть . Тогда для всех . Поэтому, 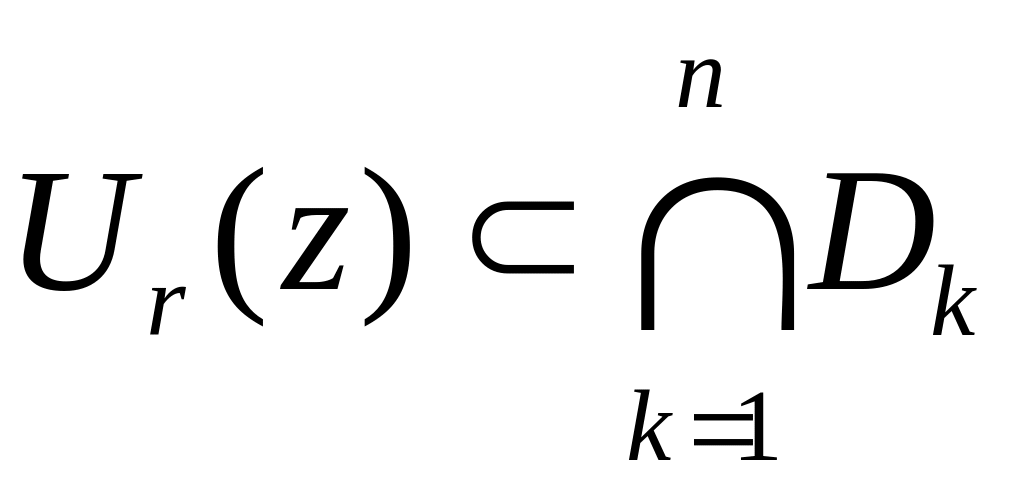и множество открыто.

Конец доказательства

Определение 1.1.11. Если на каком угодно множестве X задана система подмножеств, обладающая свойствами (1) – (3), то эту систему называют топологией в X, а отдельные множества этой системы – открытыми множествами в этой топологии. Множество X вместе с некоторой топологией называется топологическим пространством.

Конец определения.

Из определения следует, что множество комплексных чисел C вместе системой открытых множеств относительно метрики является топологическим пространством. Оно обладает еще и очевидным свойством отделимости.

Теорема 1.1.2 (Аксиома отделимости Хаусдорфа). Если и различные точки комплексной плоскости, то существуют такие окрестности и этих точек, что их пересечение пусто .

Доказательство. Рассмотрим две ‑ окрестности и такие, что , где , . Так как точки и внутренние, то можно окружить

Конец доказательства.

Определение 1.1.11. Множество всех внутренних точек множества D называется внутренней частью или внутренним ядром множества D и обозначается (от французского слова intérieur – внутренняя часть чего-либо).

Конец определения.

Если D – открытое множество, то . Очевидно, что если M открытое множество и , то . Таким образом, внутреннее ядро «самое большое» открытое множество, содержащееся во множестве D.

Определение 1.1.12. Множество всех граничных точек множества D называется границей и обозначается .

Конец определения.

Граница множества может содержать, а может и не содержать точки из множества D.

Определение 1.1.12. Множество D, содержащее все свои предельные точки или у которого они отсутствуют, называется замкнутым множеством.

Конец определения.

Определение 1.1.13. Множество всех предельных точек множества D будем обозначать .

Конец определения.

Определение 1.1.14. Множество, получающееся присоединением к множеству D всех своих предельных точек, называется замыканием множества D и обозначается .

Конец определения.

Как следует из определения замыкание . Его можно получить, объединяя множество D с множеством его предельных точек . Поэтому замыкание является всегда замкнутым множеством.

Примером замкнутого множества D является замкнутый круг с центром в точке и радиусом r

.

Пустое множество комплексных чисел или все множество комплексных чисел C не имеют предельных точек, по этому они по определению являются замкнутыми множествами так же, как и открытыми! Замкнутым множеством будет полоса и квадрат .

Теорема 1.1.1. Если к множеству D добавить все его граничные точки, то получим замыкание . Иными словами, .

Доказательство. Так как изолированные граничные точки множества D, если они существуют, всегда входят в D, то добавлять можно только те граничные точки, которые являются предельными, следовательно .

Конец доказательства.

Теорема 1.1.2. Граница любого множества комплексных точек D является замкнутым множеством, то есть .

Доказательство. Предположим противное, пусть . Это означает, что существует точка z из замыкания такая, что (то есть точка z не является граничной точкой множества D, но зато является граничной точкой границы множества D). Взяв любую проколотую ‑ окрестность точки z получим, что она содержит, так как точка z – граничная точка множества , некоторую точку . Точка y, будучи граничной точкой множества D, должна в любой своей ‑ окрестности содержать как точки из множества D, так и точки не принадлежащие D. Выбрав число достаточно малым, получим, что . Тогда в любой проколотой окрестности точки z существуют как точки из множества D, так и точки ему не принадлежащие, следовательно, точка z является граничной точкой множества D. Однако по предположению точка z не является граничной точкой множества D. Из полученного противоречия следует, что .

Конец доказательства.

Из теорем 1.1.1 и 1.1.2. следует, что граница границы – это сама граница .

Определение 1.1.15. Множество D, которое можно поместить в открытый круг конечного радиуса r, называется ограниченным множеством.

Конец определения.

Примером ограниченного замкнутого множества D является замкнутый круг с центром в точке и радиусом r

.

Определение 1.1.16. Дополнением множества D будем называть множество всех точек комплексной плоскости C, не принадлежащих D.

Конец определения.

Дополнение множества D будем обозначать символом . Из определения следует, что дополнение равно разности множеств и, следовательно, множество D и его дополнение не имеют общих точек . Очевидно так же, что дополнение от дополнения множества D есть само множество D. То есть .

Теорема 1.1.3. Если множество D открыто, то его дополнение замкнуто.

Доказательство. Дополнение либо не имеет предельные точки, либо их имеет. В первом случае является замкнутым множеством по определению. Пусть теперь у дополнения есть предельные точки. Если все предельные точки принадлежат дополнению, то по определению множество замкнуто. Пусть у дополнения найдется хоть одна предельная точка z, ему не принадлежащая. Так как множества D и не имеют общих точек, то . Точка z, как предельная точка множества , в каждой своей ‑ окрестности содержит точки множества . Но, как точка открытого множества D, она является внутренней точкой этого множества и должна иметь некоторую ‑ окрестность, целиком состоящую из точек множества D. Из полученного противоречия следует, что все предельные точки дополнения принадлежат . Следовательно, если множество D открытое, то дополнение ‑ замкнутое множество.

Пусть теперь дополнение ‑ замкнутое множество. Тогда по доказанному выше его дополнение, то есть ‑ открытое множество

Конец доказательства.

Теорема 1.1.4. Если дополнение множества D замкнуто, то множество D открыто.

Доказательство. Пусть z точка из множества D. Если точка z изолированная точка множества D, то в каждой проколотой окрестности этой точки найдутся точки, не принадлежащие D, то есть точки из дополнения . Тогда точка z – предельная точка множества . В силу замкнутости все такие точки принадлежат дополнению , а не множеству D. Из полученного противоречия следует, что у множества D нет изолированных точек. Если z граничная не изолированная точка множества D, то точка z – предельная точка не только для множества D, но и для дополнения . Но все предельные точки дополнения принадлежат ему, так как оно замкнуто. Следовательно, точки множества D могут быть только внутренними, а само множество D является открытым.

Конец доказательства.

Теорема 1.1.5. Если множество D замкнуто, то его дополнение открыто.

Доказательство. Дополнение замкнуто. Тогда по теореме 1.1.4. множество открыто.

Конец доказательства.

Теорема 1.1.6. Если дополнение множества D открыто, то множество D замкнуто.

Доказательство. Из теоремы 1.1.3. следует, что множество , как дополнение открытого множества замкнуто.

Конец доказательства.

Лемма 1.1.1 (Теорема де Моргана). Пусть ‑ конечное или бесконечное семейство множеств . Тогда

и .

Доказательство. Пусть , тогда и при всех .Следовательно, при всех , так что . Итак . Обратно, пусть . Тогда для всех и, следовательно, и . Тогда . Поэтому и . Пусть теперь . Тогда или .

Конец доказательства.

Теорема 1.1.9. Пересечение конечного или бесконечного числа замкнутых множеств является замкнутым множеством. Более того, пересечение любого семейства замкнутых множеств замкнуто.

Доказательство. Если множества семейства замкнуты, то множества семейства открыты, тогда множество открыто, а множество замкнуто. По теореме де Моргана , то есть пересечение замкнуто.

Конец доказательства.

Теорема 1.1.10. Объединение конечного числа замкнутых множеств является замкнутым множеством.

Доказательство. По теореме де Моргана . Множества открыты, тогда пересечение открыто, а дополнение замкнуто. Следовательно, замкнутое множество.

Конец доказательства.

Определение. 1.1.12. Функцией , заданной на некотором множестве вещественных чисел D и принимающей комплексные значения z на множестве E, называется правило или закон, согласно которому каждому вещественному числу ставится в соответствие комплексное число . Множества E и D называются соответственно областью значения и область определения функции .

Конец определения.

Функцию можно переписать в алгебраическом виде

,

где функции и вещественные. И, наоборот, пара вещественных функций и задает функцию .

Пусть функция определена в некоторой окрестности точки .

Определение 1.1.13. Комплексное число A называется пределом функции в точке , если для любого сколь угодно малого положительного вещественного числа найдется положительное вещественное число , такое, что из неравенства следует неравенство .

Конец определения.

Предел функции будем обозначать символом . Очевидна следующая теорема.

Теорема 1.1.2. Если , то для существования предела необходимо и достаточно одновременное существование пределов и .

Доказательство.

Необходимость. Пусть . Тогда для любого из неравенства следует неравенство . Но так как

,

,

то отсюда следует, что и .

Достаточность. Пусть существуют пределы и . Тогда для любого из неравенства следуют неравенства и . Но так как

,

то отсюда следует, что .

Конец доказательства.

Определение 1.1.14. Комплексное число A называется правым пределом (или пределом справа) функции в точке , если для любого сколь угодно малого положительного вещественного числа найдется положительное вещественное число , такое, что из неравенства следует неравенство .

Конец определения.

Правый предел функции будем обозначать символом . Так же часто используются обозначения , , или .

Определение 1.1.15. Комплексное число A называется левым пределом (или пределом слева) функции в точке , если для любого сколь угодно малого положительного вещественного числа найдется положительное вещественное число , такое, что из неравенства следует неравенство .

Конец определения.

Левый предел функции будем обозначать символом . Так же часто используются обозначения , , или .

Очевидна следующая теорема, доказываемая аналогично теореме 1.1.2.

Теорема 1.1.3. Если , то для существования правого предела (левого предела ) необходимо и достаточно одновременное существование правых пределов и (левых пределов и ).

Определение 1.1.13. Путем Г называется непрерывное отображение отрезка действительной оси во множество комплексных чисел.

Конец определения.

Из определения следует, что путь – это функция , принимающая комплексные значения z, и имеющая вещественный аргумент t, принимающий значения из отрезка .