Вопрос 3.2. Показательная форма комплексного числа. Формула Эйлера.

Показательная форма комплексного числа основана на формуле Эйлера

, (25)

где e=2,71828182845904523546... иррациональное число. Формула (25) будет доказана в разделе «Функции комплексного переменного» и здесь приводится без доказательства. Используя формулу (25) и тригонометрическую форму получим

. (26)

Формула (26) называется показательной формой комплексного числа. В этой форме удобно выполнять умножение и деление комплексных чисел

, (27)

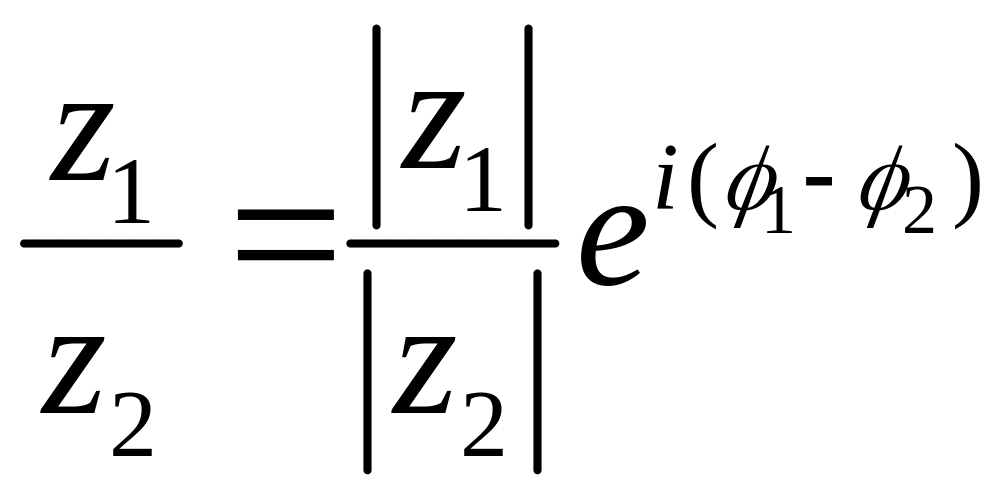. (28)

Вопрос 3.3. Корень целой степени из комплексного числа.

Определение 3.3. Корнем, целой степени n из комплексного числа z называется комплексное число w такое, что

(1)

Теорема 3.1. Существует ровно n различных корней из комплексного числа , значения которых даются формулой

(2)

(3)

Доказательство. Пусть комплексные числа w и z представлены в показательной форме

и

Тогда, подставляя в формулу (1), получим

Но равенство двух комплексных чисел означает, что равны их модули, а аргументы различаются на число кратное 2

, (4)

, k ‑ целое число. (5)

Отсюда получим

(6)

, k ‑ целое число. (7)

Если , то по формуле (7) получаются аргументы, отличающиеся друг от друга на число не кратное 2. Следовательно, имеется n аргументов, отвечающих разным значениям корня n-й степени из комплексного числа. Если или то новый аргумент будет отличаться от одного из аргументов с на число, кратное , то есть вновь получим один из n различных корней числа z. То же верно и для целого .

Конец доказательства.

Пример 3.1. Вычислить корень квадратный из отрицательного вещественного числа D.

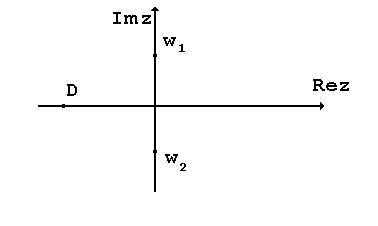
Рис. 1.

Если D<0, то, как видно из рис. 1, arg D=. Тогда получаем два значения квадратного корня

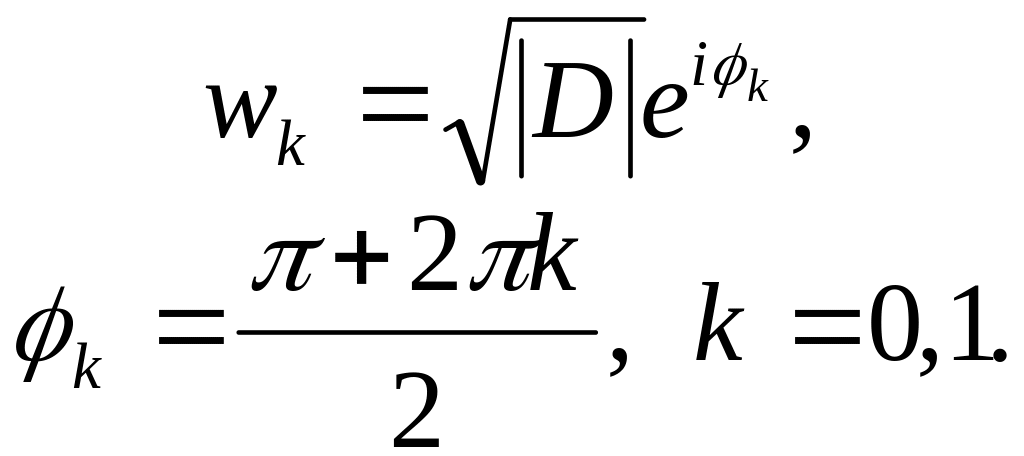
Эти корни можно переписать в виде

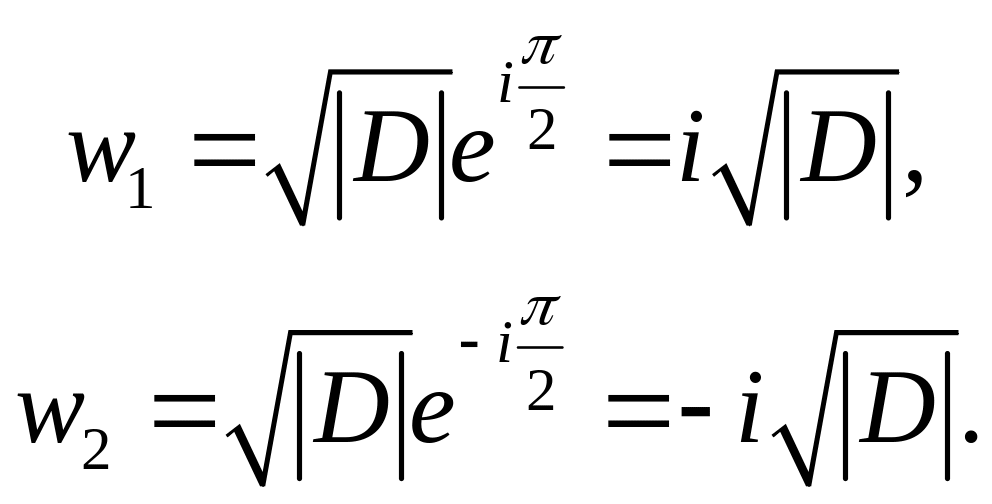
Пример 2. Корни квадратного уравнения с отрицательным дискриминантом D.

Пусть дискриминант квадратного уравнения

отрицателен. Если выделить полный квадрат, то получим для квадратного корня обычную формулу

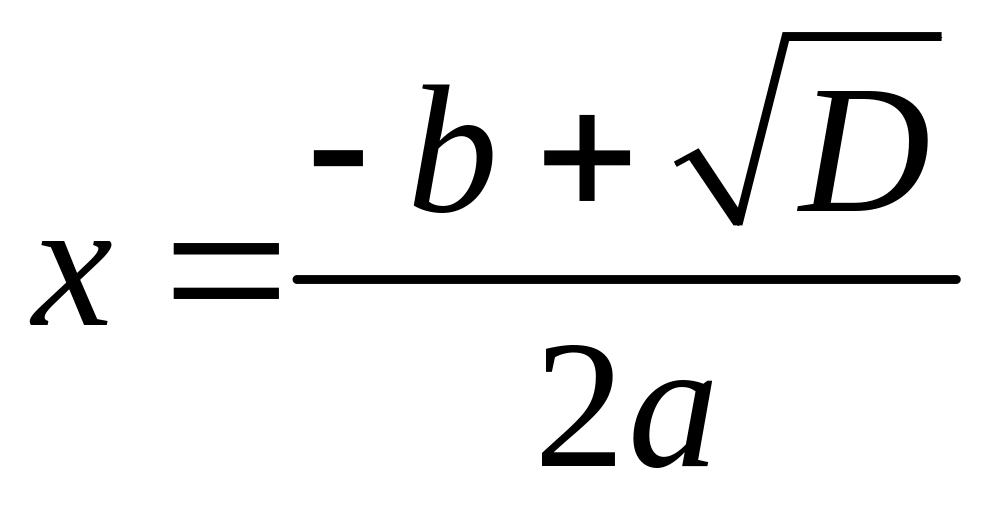
Если , то мы должны извлекать квадратный корень с комплексными значениями. Используя результат примера 1, получим

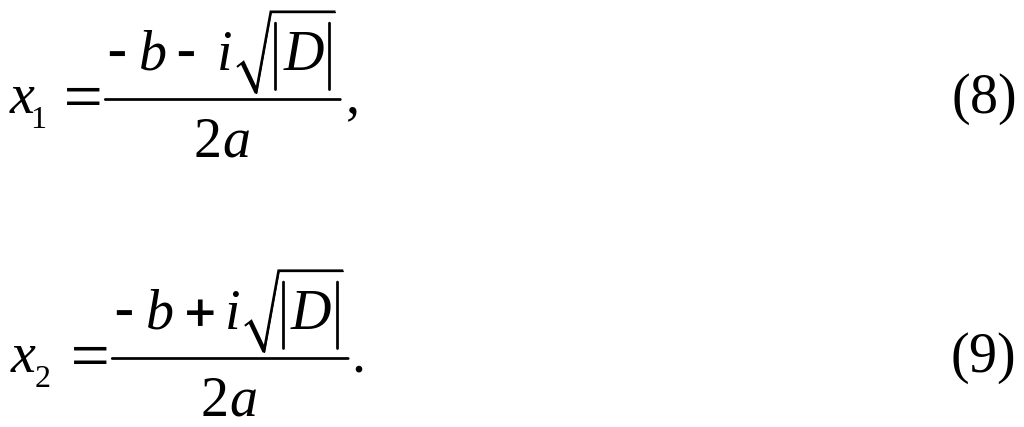
Лекция № 4. Матричное исчисление. Определители.

Вопрос 4.1. Матрицы и действия над ними.

Опредление 4.1. Матрицей размера называется прямоугольная таблица чисел, состоящая из m строк и n столбцов

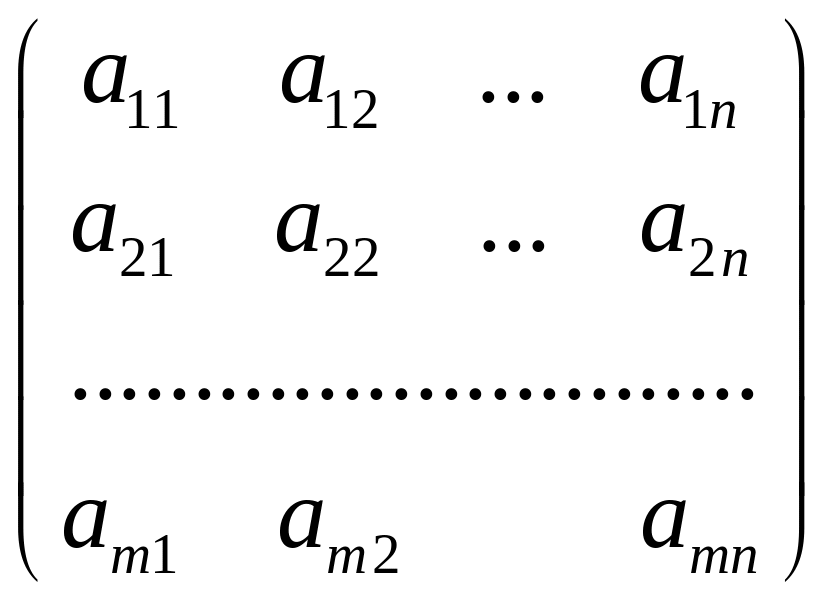
Числа, составляющие таблицу, называются элементами матрицы. Матрицы обозначаются большими латинскими буквами A, B, C ... , а их элементы ‑ малыми латинскими буквами a, b, c ....

Каждый элемент матрицы нумеруется двумя числами, которые называются индексами или указателями:

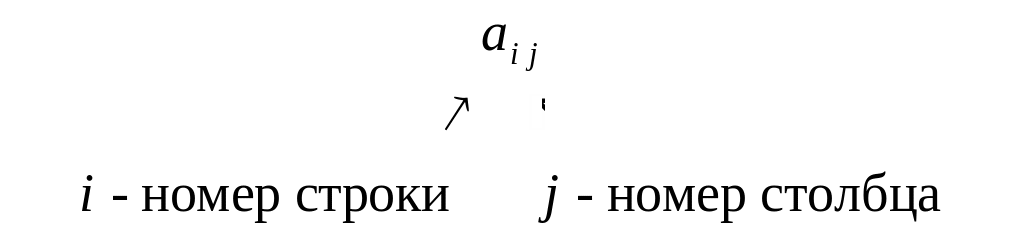
первый индекс указывает на номер строки, а второй ‑ на номер столбца. Если элементы матрицы состоят из вещественных или комплексных чисел, то матрица называется соответственно вещественной или комплексной.

Нулевая матрица ‑ матрица, состоящая из нулевых элементов, обозначается 0.

Квадратная матрица ‑ матрица размера .

Треугольная матрица ‑ квадратная матрица, у которой все элементы, расположенные ниже или выше главной диагонали, равны нулю.

Диагональная матрица ‑ квадратная матрица, у которой все элементы, расположенные вне главной диагонали равны нулю.

Единичная матрица ‑ диагональная матрица, диагональные элементы которой равны единице.

Над матрицами определены следующие действия: сложение, вычитание, умножение на число и на матрицу.

Опредление 4.2. Матрица C есть сумма матриц A и B, если все три матрицы одинакового размера и

Тогда пишут . Сложение матриц подчиняется двум законам

‑ коммутативный закон сложения,

‑ ассоциативный закон сложения.

Доказательство. Пусть и . Тогда и

.

Опредление 4.3. Матрица C есть разность матриц A и B, если все три матрицы одинакового размера и

Тогда пишут .

Опредление 4.4. Матрица C есть произведение числа  на матрицу A, если обе матрицы одинакового размера и

Тогда пишут . Легко доказать следующие равенства

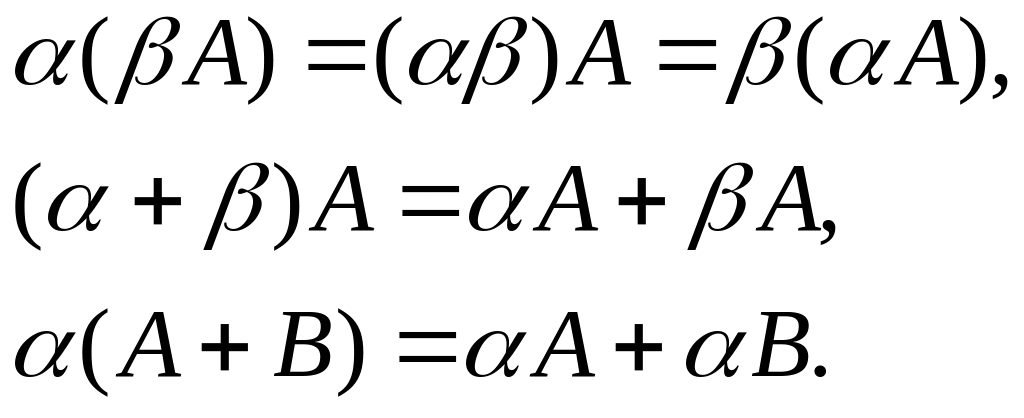
Доказательство.

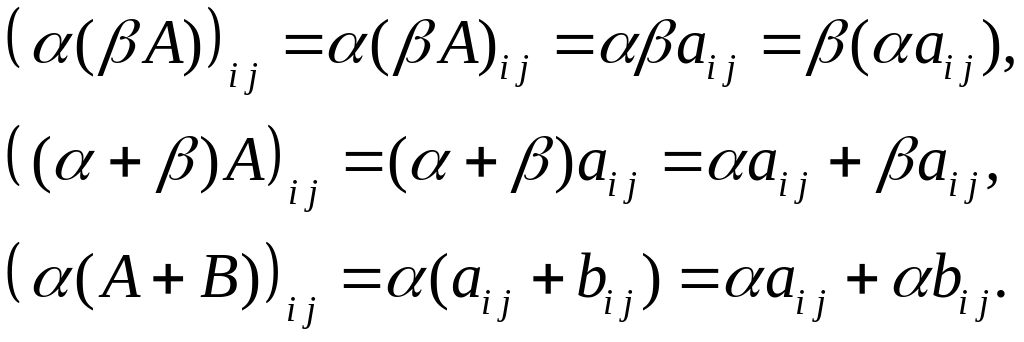
Конец доказательства.

Пример 4.1. Вычислить матричное выражение , где

.

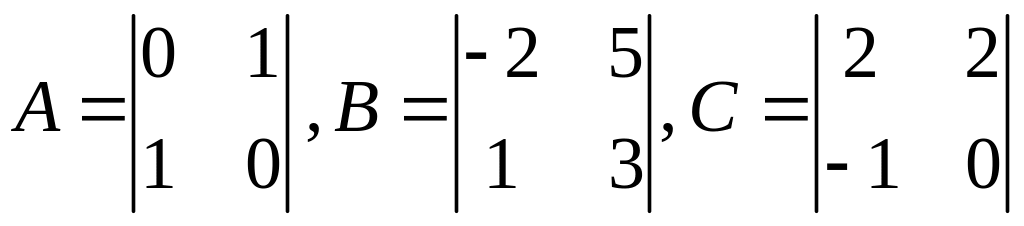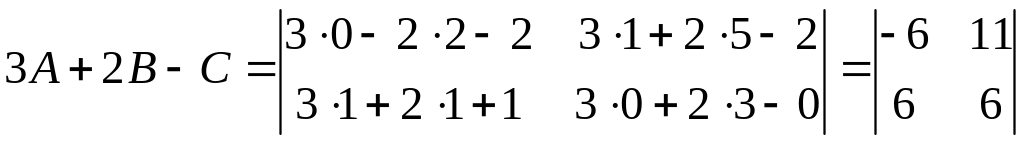
Конец примера.

Для дальнейшего изложения нам потребуется знак суммирования для сокращенного обозначения суммы чисел

.

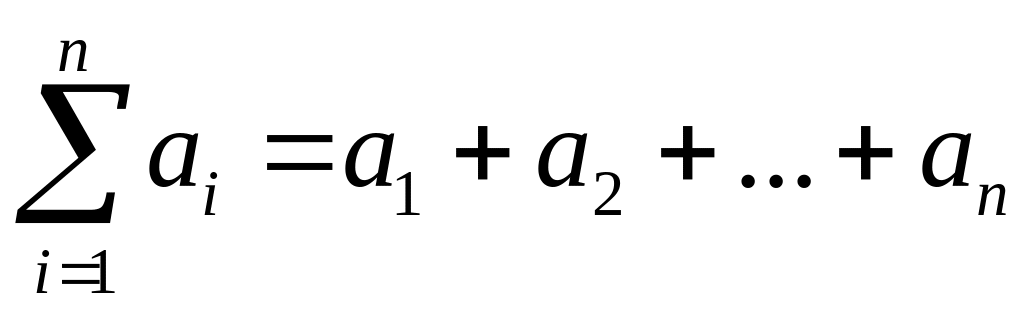Докажем следующие свойства операции суммирования, основанные на переместительном, сочетаельном и распределительном законах сложения и умножения, то есть на возможности как угодно переставлять слагаемые и выносить общие множители за скобки:

1) ,

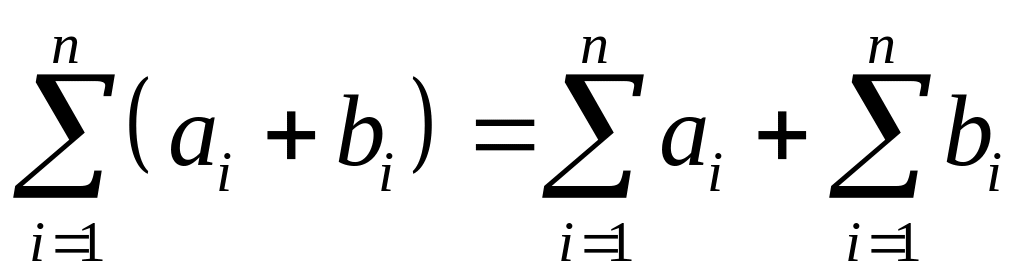2) ,

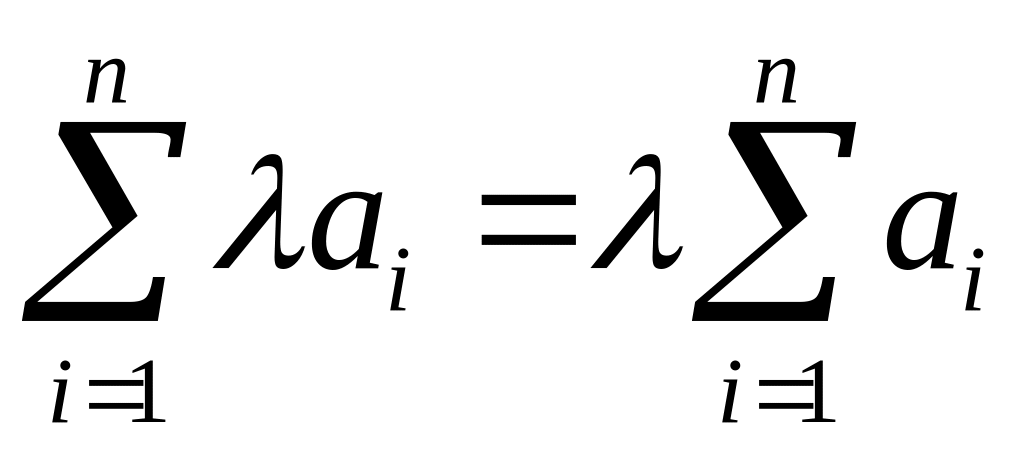3) .

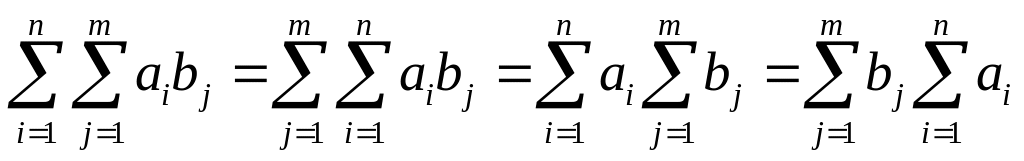Доказательство.

1)

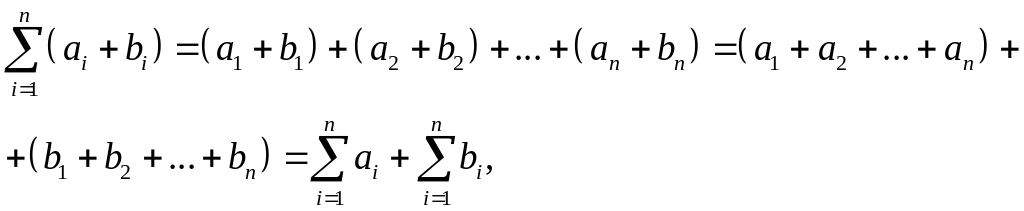
2)

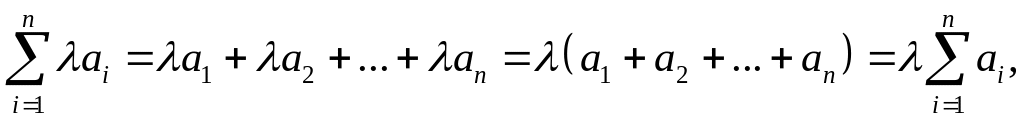
3)

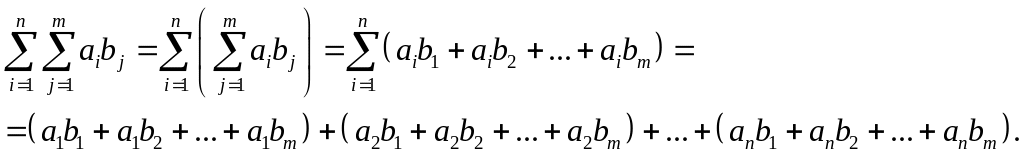
Сгрупперуем теперь слогаемые, собирая сначала члены, содержащие общие множители

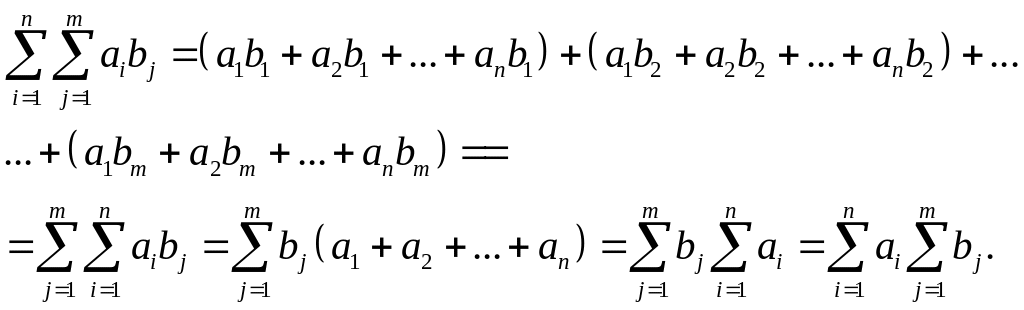
Опредление 4.5. Матрица C размером называется произведением матриц A и B, если две последние имеют согласованные размеры и соответственно и

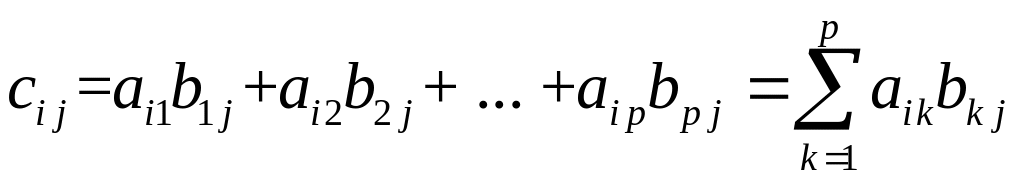(4.1)

Тогда пишут . В формуле (4.1) используются элементы i строки матрицы A и элементы j столбца матрицы B, то есть строки первой матрицы "перемножаются" на столбцы второй матрицы. Из определения произведения матриц следует, что перемножать можно матрицы, у которых число столбцов первой матрицы равно числу строк второй матрицы.

Матричное умножение подчиняется следующим законам:

1)  ‑ ассоциативный закон произведения,

2)  ‑ дистрибутивный закон умножения относительно сложения.

Доказательство.

1) Пусть даны матрицы A, B и С соответственно размеров , и . Тогда

.

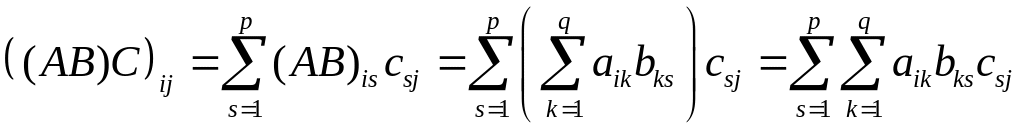Поменяв местами порядок суммирования, получим

,

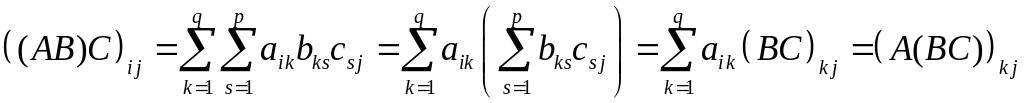откуда следует равенство .

2) Пусть даны матрицы A, B и С соответственно размеров , и . Тогда

.

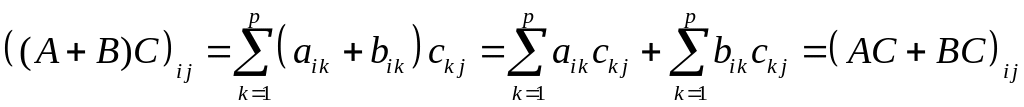Конец доказательства.

Внимание! Матричное произведение не коммутативно, то есть матричные множители нельзя в общем случае менять местами.

Опредление 4.6. Квадратные матрицы и одинакового размера называются коммутирующими, если .

Опредление 4.7. Коммутатором квадратных матриц и одинакового размера называется разность .

Очевидно, что если коммутатор , то матрицы и коммутируют и обратно, если матрицы и коммутирующиеся, то их коммутатор равен нулю .

Пример 4.2. Вычислить произведения AB и BA, есл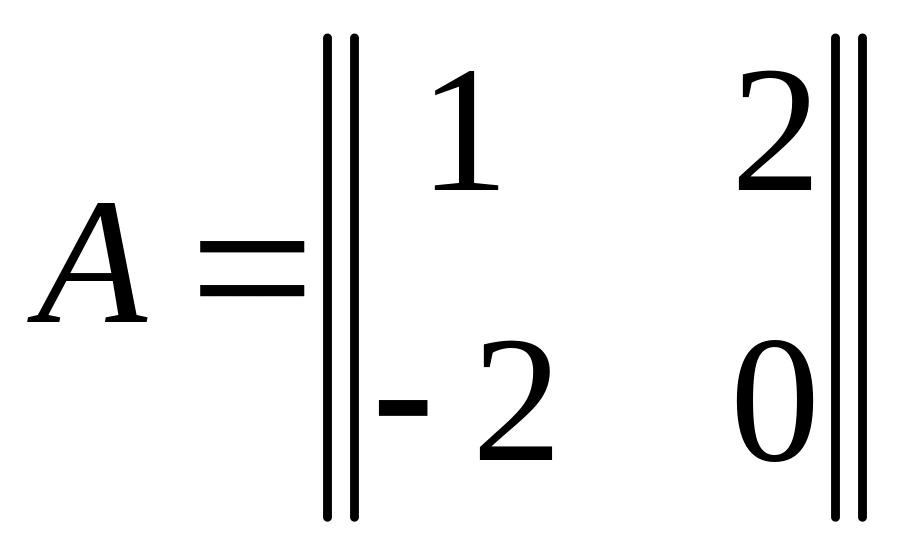и

и .

,

,

.

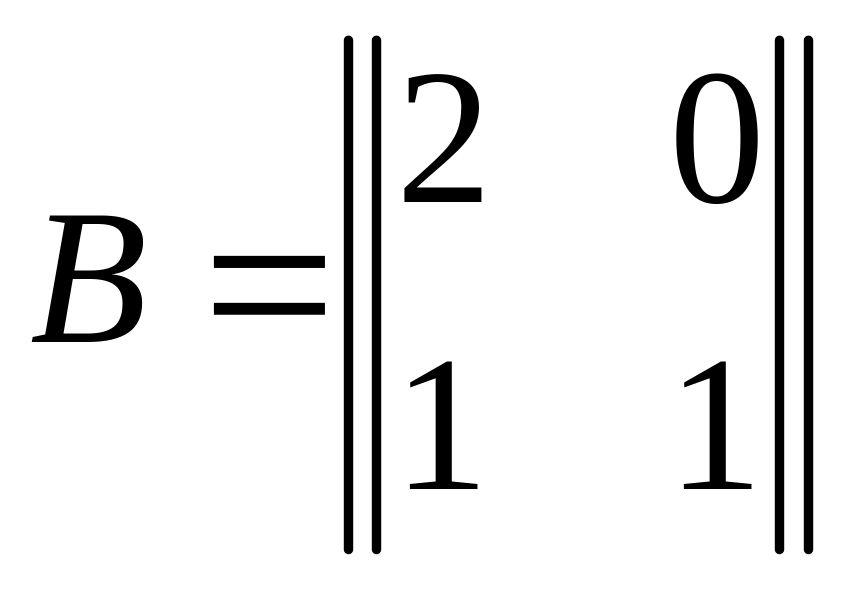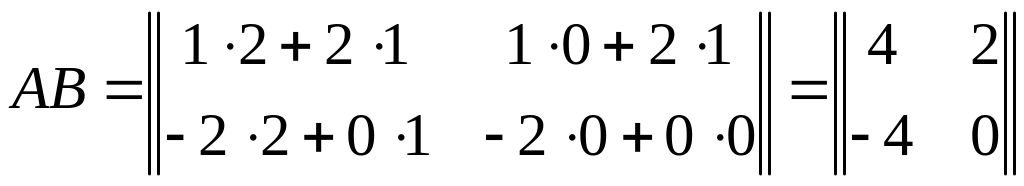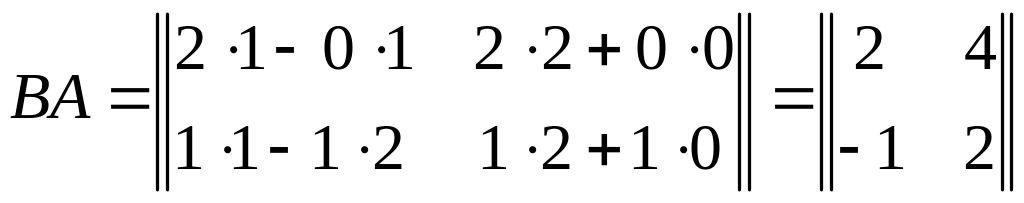Конец примера.

Опредление 4.8. Транспонированием матрицы называется операция замены строк на столбцы. Будем обозначать символом транспонированную матрицу A. Тогда элементы этих матриц связаны равенством

.

Если матрица квадратная, то транспонирование сводится к вращению матрицы на 180 градусов относительно главной диагонали. Операция транспонирования обладает следующими свойствами

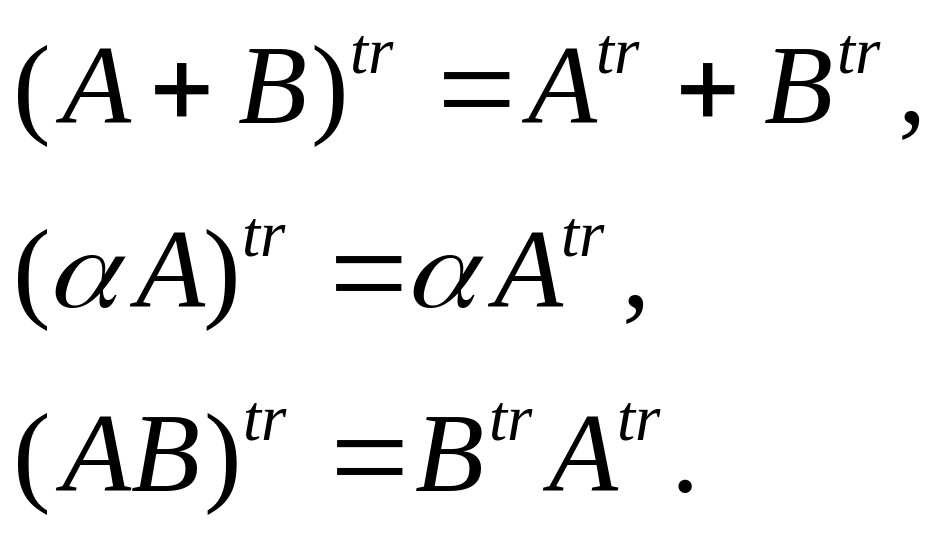
Доказательство.

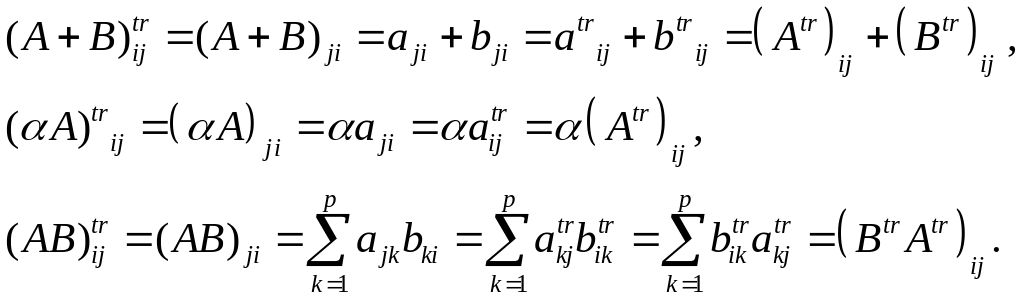
Конец доказательства.

Опредление 4.9. Матрица называется сопряженной (реже эрмитово сопряженной) к матрице A, если она получена из матрицы A путем транспонирования и комплексного сопряжения ее элементов

.

Операция сопряжения обладает следующими свойствами

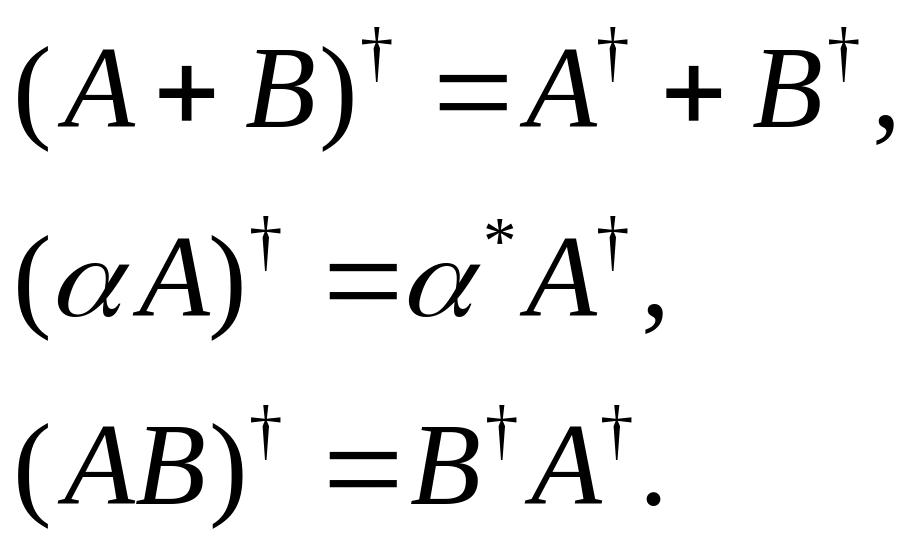
Доказательство.

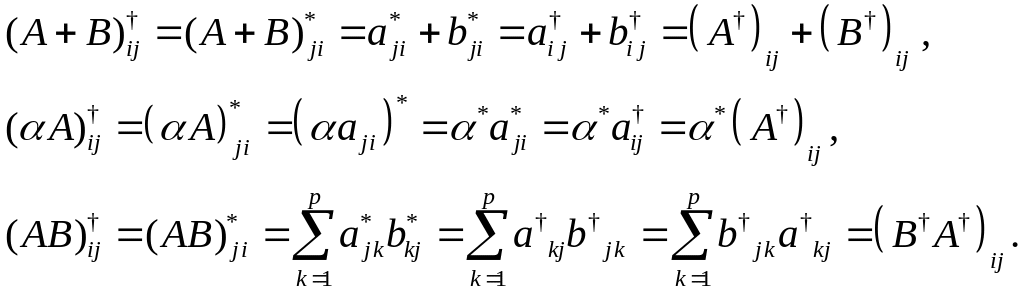
Конец доказательства.

Опредление 4.10.  Квадратная вещественная матрица A называется симметричной, если она равна своей транспонированной .

Из определения следует, что у симметричной матрицы элементы, расположенные симметрично относительно главной диагонали равны .

Опредление 4.11.  Квадратная комплексная матрица A называется самосопряженной (реже эрмитовой), если она равна своей сопряженной .

Из определения следует, что у самосопряженной матрицы элементы, расположенные симметрично относительно главной диагонали комплексно сопряжены , а элементы, стоящие на главной диагонали, вещественны .