Вопрос 2.2. Алгебраическая форма комплексного числа.

Рассмотрим комплексные числа с . Легко убедиться, что справедливы равенства

Определим теперь операции вычитания и деления комплексных чисел

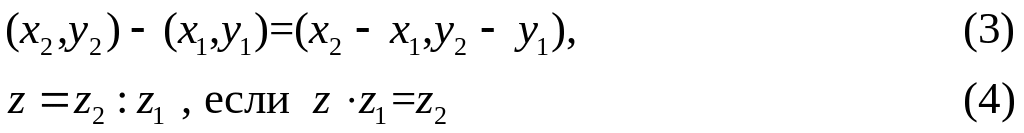
Для комплексных чисел с мнимой частью формула (3) принимает вид

Рассмотрим теперь формулу (4). Пусть , тогда или , отсюда . Откуда . Поэтому .

Из рассмотренного ясно, что действия над комплексными числами соответствуют действиями над вещественными числами x, и поэтому можно отождествить вещественные числа с комплексными числами . Будем в дальнейшем писать вместо пары число x.

Далее, комплексное число можно записать в виде произведения

Число называется мнимой единицей и обозначается

. (8)

Теперь формулу (7) можно переписать

(9)

Пусть теперь дано произвольное комплексное число , тогда

.

Используя формулы (6) и (9), получим

. (10)

Формула (10) является алгебраической формой представления комплексного числа. В этой форме легко выполнять алгебраические действия над комплексными числами по обычным правилам алгебры вещественных чисел, с учетом равенства

, (11)

которое получается умножением по правилу умножения комплексных чисел.

Пример 2.2. Вычислить выражение .

Раскроем скобки , следовательно, .

Конец примера.

Введем новую операцию комплексного сопряжения

, (12)

которая заключается в изменении знака мнимой части на противоположный. Используется и другое обозначение

.

Несложно доказать следующие равенства

, (13)

, (14)

, (15)

, (16)

Покажем, как с помощью операции комплексного сопряжения можно выполнить деление комплексных чисел. Сначала докажем, что при делении комплексного числа на вещественное число, нужно на последнее поделить отдельно вещественную и мнимую части

.

Пусть , тогда, по определению операции деления

Отсюда,

поэтому

.

Пусть теперь нужно выполнить деление .

Умножим числитель и знаменатель на число комплексно сопряженное знаменателю

Теперь знаменатель стал вещественным и нужно выполнить деление вещественной и мнимой частей, как описано выше.

Пример 2.3. Выполнить деление

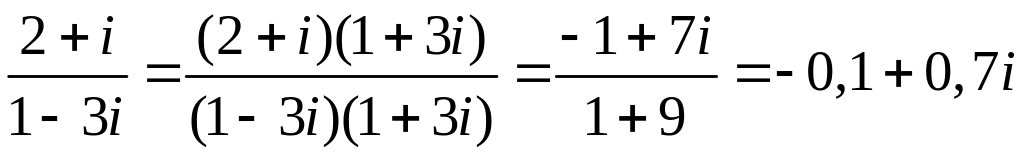
Конец примера.

ЛЕКЦИЯ № 3. КОМПЛЕКСНЫЕ ЧИСЛА.

Вопрос 3.1. Тригонометрическая форма комплексного числа.

Комплексным числам можно дать геометрическую интерпретацию, если рассматривать каждое комплексное число как точку плоскости (или вектор) с координатами (см. рис. 1).

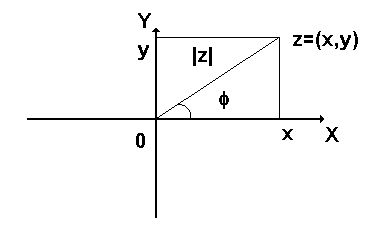
Рис. 1. Геометрическая интерпретация комплексного числа.

Расстояние от начала системы координат до точки, соответствующей комплексному числу , называется модулем комплексного числа и обозначается

(17)

Определение 3.1. Угол между осью X и радиус-вектором, соединяющим точку , называется аргументом комплексного числа. Очевидно, угол  удовлетворяет системе уравнений

Более точно, аргументом комплексного числа называется величина, удовлетворяющая системе (18) ‑ (19). Как видно из системы (18) ‑ (19), если есть аргумент числа z, то и , где n целое число, является аргументом того же самого числа. Для однозначности аргумент выбирают в пределах

(20)

и обозначают . Тогда любое комплексное число можно представить в тригонометрической форме

(21)

Комплексное число можно представить в тригонометрической форме , однако аргумент одназначно определить не возможно.

Пример 3.1. Представить число в тригонометрической форме.

Вычислим модуль

.

Найдем аргумент из системы уравнений

Поделим второе уравнение на первое, получим

откуда

или

Системе уравнений удовлетворяет значение . Следовательно, тригонометрическая форма имеет вид

.

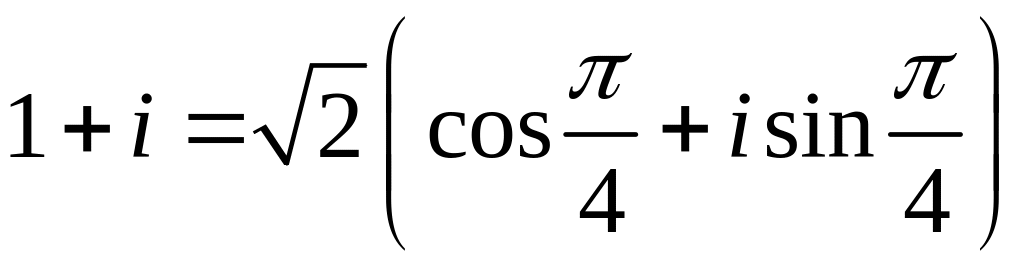Конец примера.

В тригонометрической форме удобно выполнять умножение и деление, так как справедливы равенства

,………………(22)

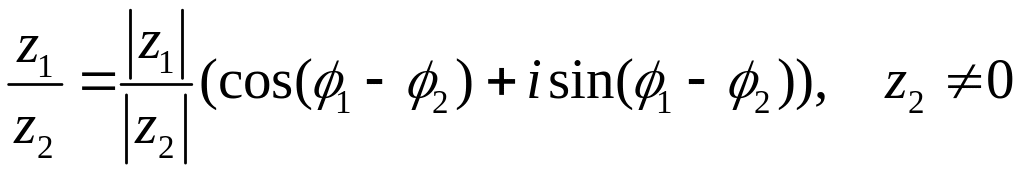. (23)

Докажем эти формулы.

Доказательство. Пусть и . Тогда

.

Для комплексного числа , обратным будет комплексное число

.

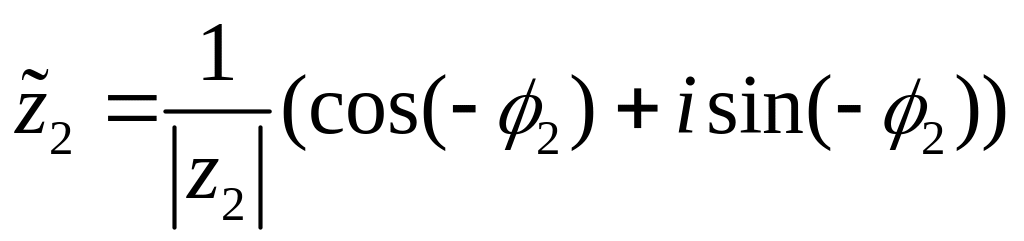Действительно,

.

Поэтому,

.

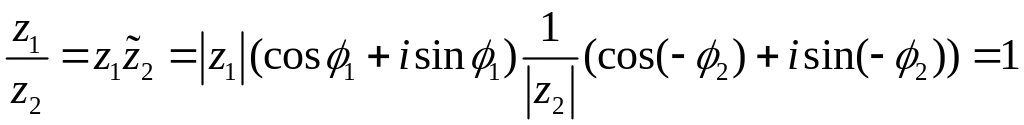
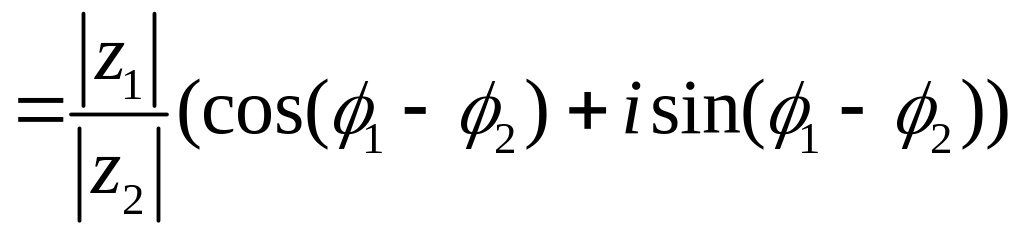Конец доказательства.

Из формулы (22) следует формула Муавра

, (24)

где n целое число.

Доказательство. Для натурального n докажем формулу Муавра по индукции. Для формула, очевидно, верна. Пусть формула верна для некоторого натурального числа . Докажем, что тогда она верна и для натурального числа .

.

Для целого отрицательного n получаем

.

Конец доказательства.

Используя формулу Муавра, легко получить некоторые тригонометрические формулы, например

но

откуда, сравнивая отдельно действительные и мнимые части, получим известные формулы

.