Вопрос 17.2. Бесконечно малые и бесконечно большие функции.
Определение
17.3. Функция
называется бесконечно малой в окрестности
точки b
(в том числе
,
,
),
если
Определение 17.4. Функция называется бесконечно большой в окрестности точки b (в том числе , , ), если
Теорема 17.3.
Если функция
бесконечно малая в окрестности точки
b,
то
бесконечно большая в окрестности точки
b.
Теорема 17.4. Если функция бесконечно большая в окрестности точки b, то бесконечно малая в окрестности точки b.
Докажите эти теоремы самостоятельно.
Пример 17.2.
Функция x
бесконечно малая в окрестности
,
функция
бесконечно большая в окрестности
.
Теорема 17.5.
Если A
есть предел функции
в точке b,
то
,
где
бесконечно
малая функция, то есть
Доказательство.
Положим
,
тогда
.
Конец доказательства.
Вопрос 17.3. Сравнение функций. O-символика.
Определение
17.4. Пусть
и
две бесконечно малые функции в окрестности
точки b.
Функция
имеет более высокий порядок малости,
чем
,
если
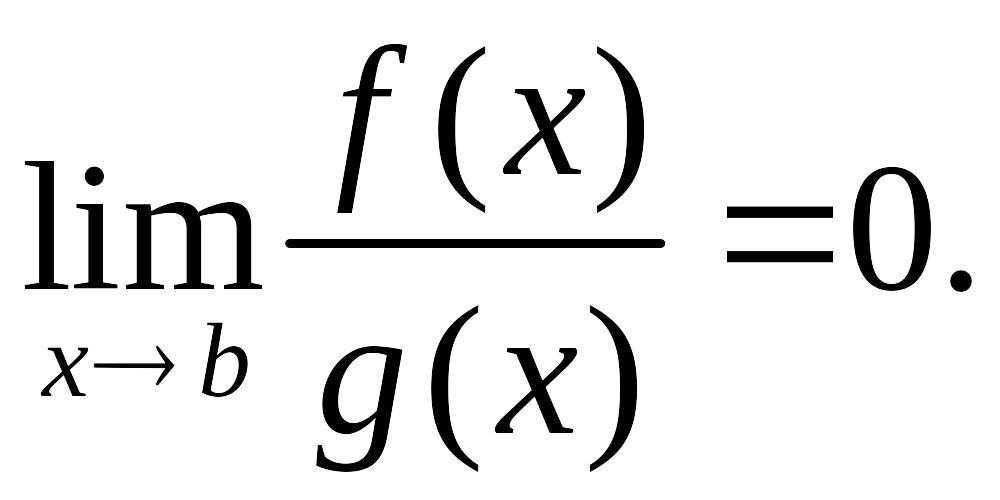
В этом случае
пишут
.
Определение 17.5. Пусть и две бесконечно малые функции в окрестности точки b. Функция имеет одинаковый порядок малости с , если
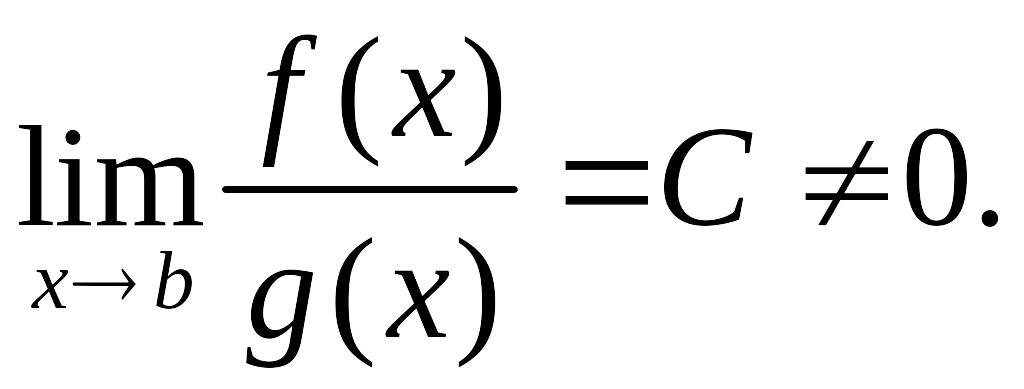
В этом случае
пишут
.
Определение
17.6. Две
функции
и
называются асимптотически равными или
эквивалентными при
,
если
.
Эквивалентные функции будем обозначать знаком ~ .
Пример 17.3.
Пусть
,
.
Так как
то
.
Конец примера.
Теорема 17.6.
Если
при xb,
то
если
последний предел существует или равен
бесконечности.
Доказательство. Так как
,
то
поскольку
Конец доказательства.
Замечание. Теорема утверждает, что можно при вычислении пределов заменять множители эквивалентными им функциями. Слагаемые менять нельзя.
Пример 17.4.
Вычислить
где
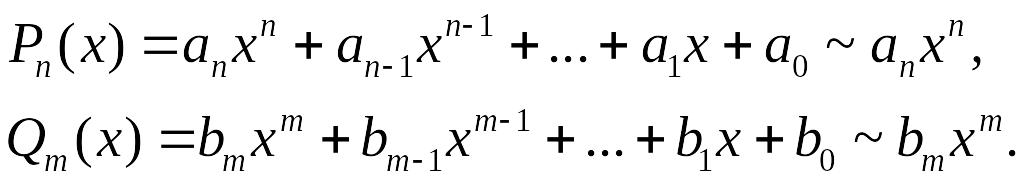
Конец примера.
Вопрос 17.4. 1-й и 2-й замечательный пределы.
Следующие два предельных перехода называются соответственно 1-м и 2-м замечательными пределами
где e=2,718281828459045... ‑ иррациональное число. Доказательство этих пределов опускается.
1-й замечательный предел можно так же представить в виде
.
Докажите это самостоятельно. 2-й замечательный предел можно представить в одном из трех видов
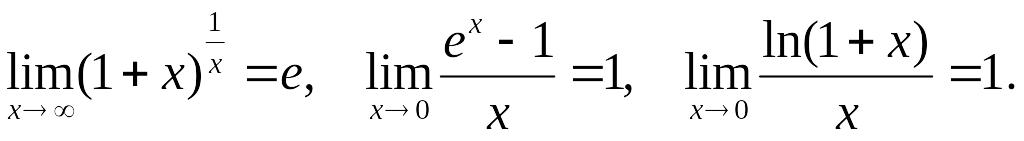
Пример 17.5. Вычислить предел.
.
При вычислении предела воспользовались эквивалентностью функций
.
Конец примера.
Лекция № 18. Функции одной переменной.
Вопрос 18.1. Точки разрыва.
Определение 18.1. Точка a называется точкой разрыва функции , если эта точка не является точкой непрерывности функции .
Точки разрыва делятся на два рода (см. рис. 1):
1) точки разрыва первого рода ‑ это точки, в которых существуют одновременно левый и правый предел функции; среди точек разрыва первого рода выделяют точки устранимого разрыва, в которых левый предел равен правому;
2) точки разрыва второго рода ‑ это точки разрыва, в которых один из односторонних пределов не существует или равен бесконечности;
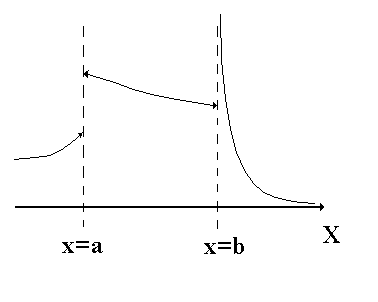
Рис. 1. Точки
разрыва:
‑
первого рода,
‑ второго
рода.
Пример 18.1.
1) 
есть точка устранимого разрыва, поскольку
;
2)
есть точка разрыва 2-го рода, так как
,
3)
,
эта функция принимает значение 1, если
,
значение
,
если
,
значение 0, если
;
эта точка является точкой разрыва 1-го
рода, так как
,
.
Конец примера.