Лекция № 14. Числовые последовательности.

Вопрос 14.1. Основные определения теории числовых последовательностей.

Определение 14.1. Пусть X и Y два множества произвольной природы. Функцией на множестве X, принимающей значения из множества Y, называется правило или закон f, по которому каждому элементу x из множества X ставится в соответствие некоторый элемент y из Y. Множество X называется областью определения функции, а множество Y называется областью изменения функции f.

Определение 14.2. Пусть ‑ множество натуральных чисел, или множество вещественных или комплексных чисел. Тогда функция натурального аргумента называется числовой последовательностью.

Если натуральному числу n соответствует число u, то мы будем называть это число n-м членом последовательности и писать , а саму последовательность будем задавать списком:

или кратко .

Над последовательностями определены операции сложения, вычитания, умножения, деления и умножения на число. Если даны три последовательности

то можно определить операции так

сложение

вычитание

умножение

деление

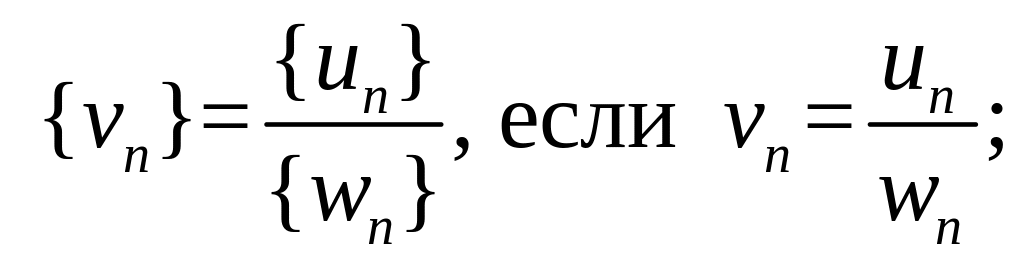
умножение на число

Определение 14.3. Числовая последовательность называется ограниченной, если существует число , такое, что для всех n.

Для вещественной последовательности можно определить ограниченность сверху и снизу.

Последовательность ограничена сверху, если существует число M такое, что для любого n выполняется неравенство .

Последовательность ограничена снизу, если существует число M такое, что для любого n выполняется неравенство .

Для вещественных последовательностей вводится понятие монотонности:

монотонно возрастающая последовательность ‑ ,

монотонно убывающая последовательность ‑ ,

монотонно неубывающая последовательность ‑ ,

монотонно невозрастающая последовательность ‑ .

Пример 14.1. Последовательность является монотонно убывающей и ограниченной .

Конец примера.

Вопрос 14.2. Предел числовой последовательности.

Начнем с примера. Пусть дана последовательность с n-м членом 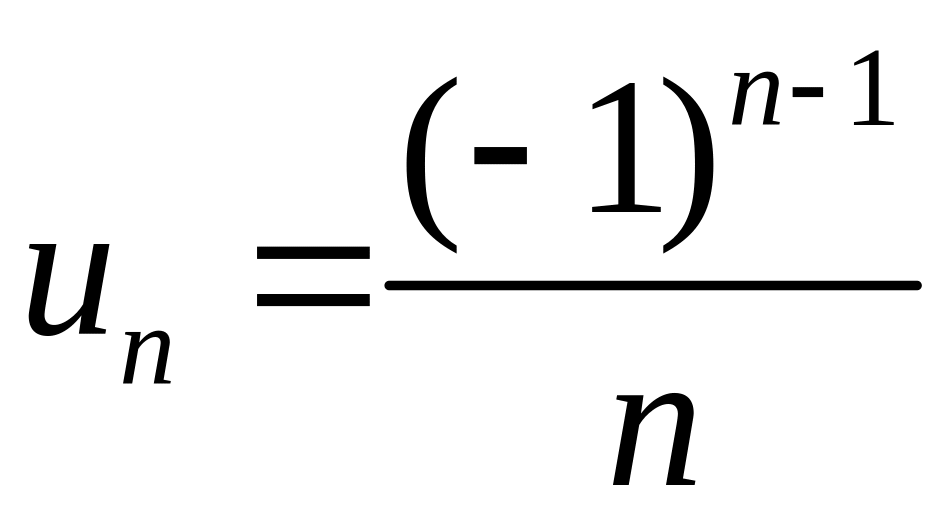. На числовой оси члены последовательности располагаются так

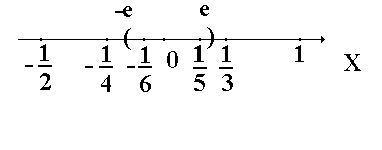
Мы видим, что члены последовательности сгущаются около точки 0, так что внутри любого сколь угодно малого отрезка содержится бесконечно большое число членов последовательности, а вне его ‑ лишь конечное число членов последовательности.

Определение 14.4. Число u называется пределом последовательности , если для любого существует число , такое что из неравенства следует выполнение неравенства . Этот записывают так:

.

Если последовательность комплексная, то означает модуль комплексного числа.

Пример 14.2. Пусть дана последовательность .

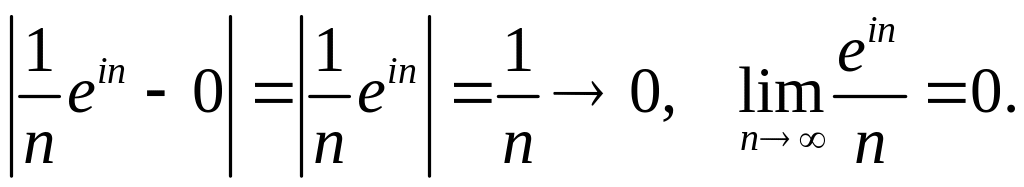
Определение 14.5. Если последовательность имеет предел, то она называется сходящейся, если нет ‑ то расходящейся.

Для расходящейся последовательности, как это следует из определения 14.4, вне -окрестности любой точки a, то есть вне множества , лежит бесконечно много членов последовательности.

Определение 14.6. Если последовательность имеет конечный предел, то она называется сходящейся, в противном случае ‑ расходящейся.

Перечислим свойства сходящихся последовательностей:

1) Сходящаяся последовательность имеет всегда один предел и ограничена.

2) Предел сходящейся последовательности, n-й член которой принимает постоянное значение, равен этой константе:

, если для всех n.

3) Сумма или разность двух сходящихся последовательностей является сходящейся последовательностью, причем предел суммы или разности сходящихся последовательностей равен сумме или разности их пределов

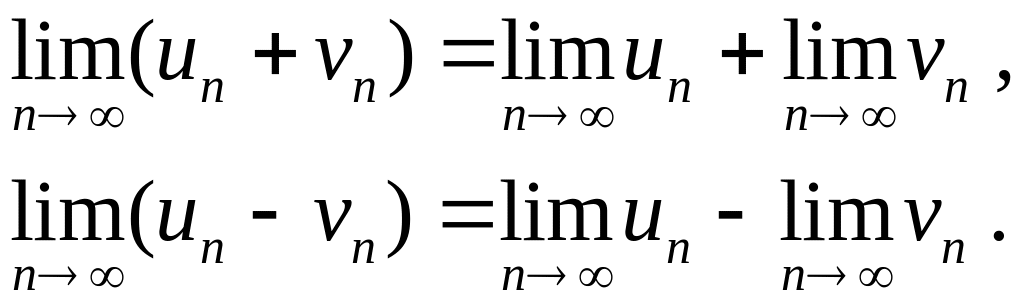
4) Произведение сходящихся последовательностей является сходящейся последовательностью, предел произведения сходящихся последовательностей равен произведению их пределов:

5) Частное от деления двух сходящихся последовательностей является сходящейся последовательностью, причем предел частного от деления двух сходящихся последовательностей равен частному от их пределов, если предел последовательности в знаменателе не равен нулю

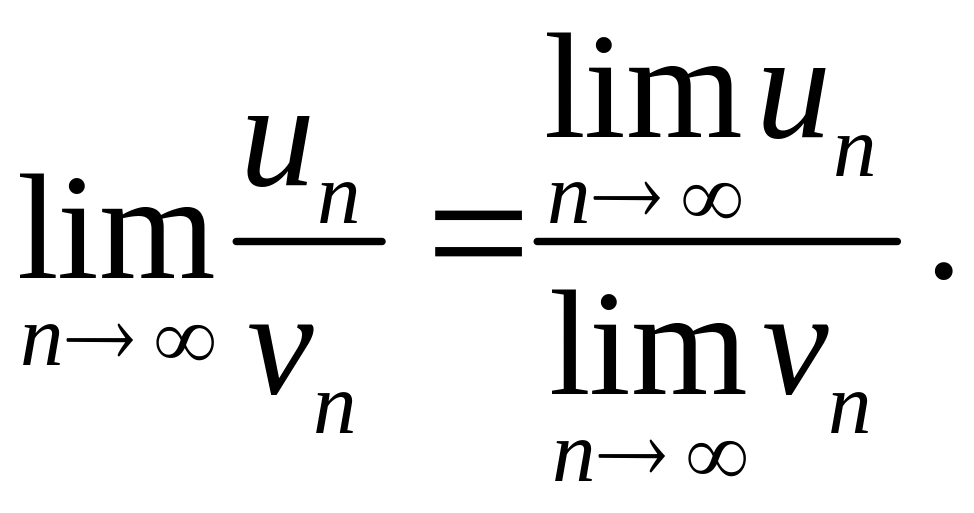
6) Если n‑е члены сходящихся последовательностей, начиная с некоторого n, связаны неравенством , то их пределы тоже связаны неравенством .

Пример 14.3.

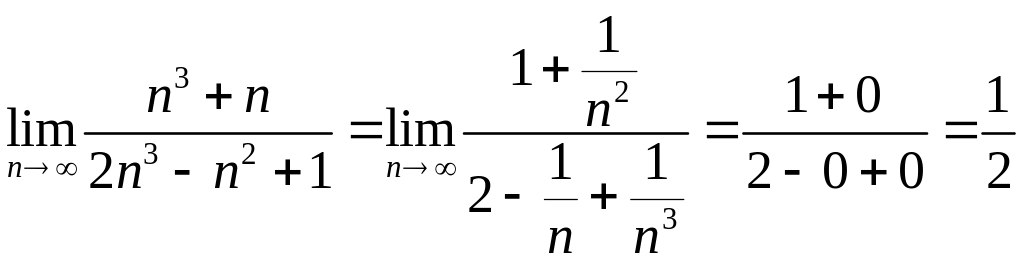
Конец примера.

Справедлива теорема о сходимости монотонной последовательности:

Теорема 14.1. Если монотонная последовательность ограничена, то она сходится.

Пример 14.4. Доказать сходимость числовой последовательности .

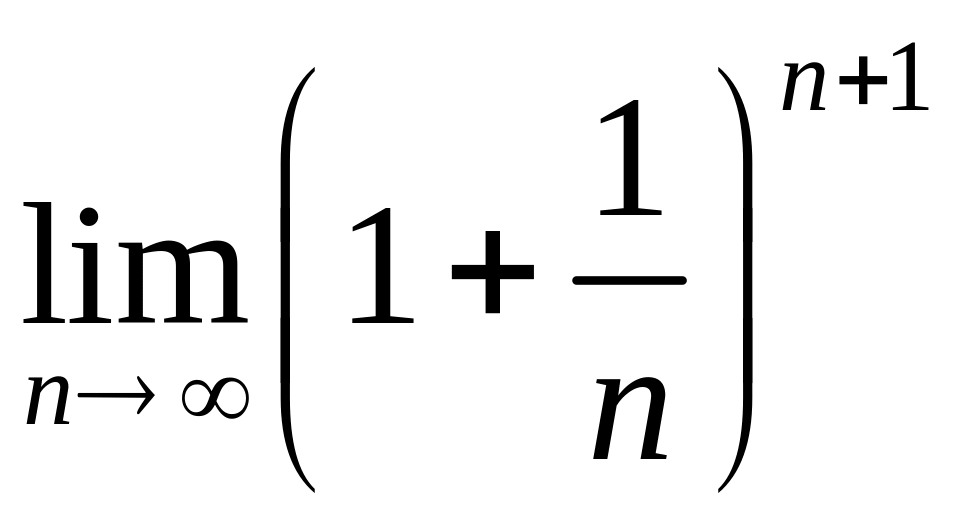Для доказательства установим методом математической индукции для всех натуральных n справедливость следующего неравенства Бернулли 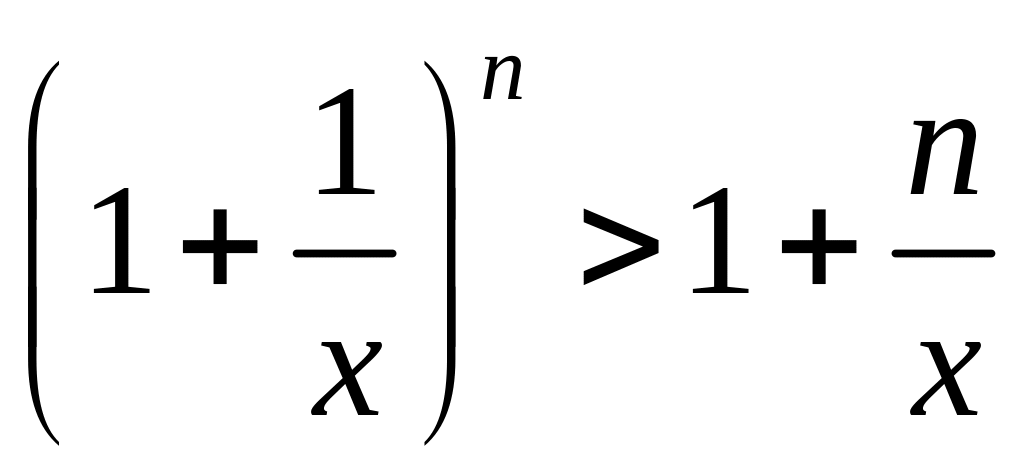. Действительно, при 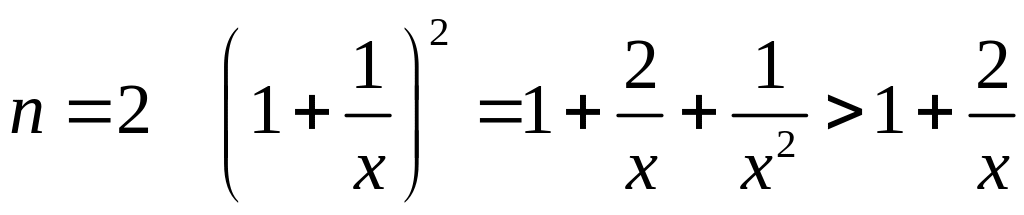неравенство верно. Пусть оно справедливо для , то есть 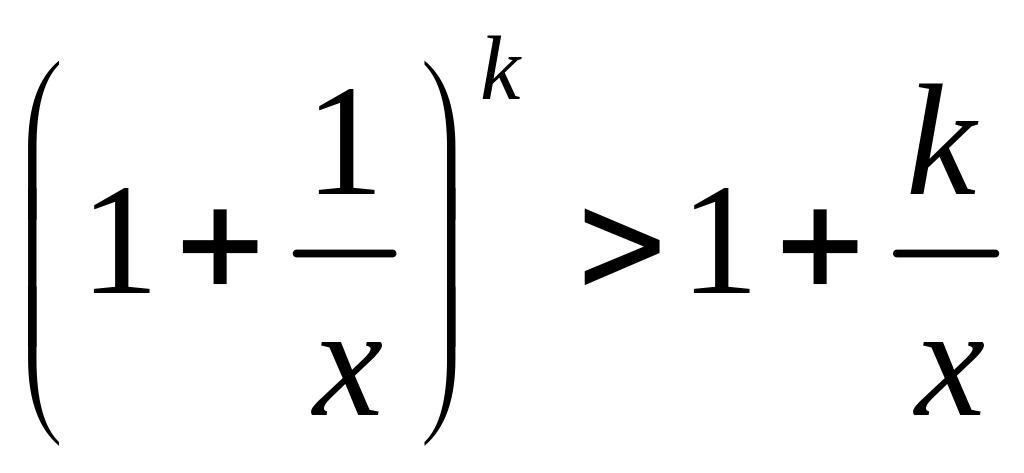. Докажем его справедливость для .

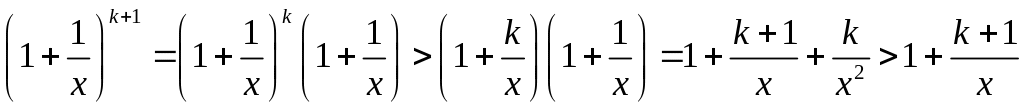
Неравенство доказано. Пусть 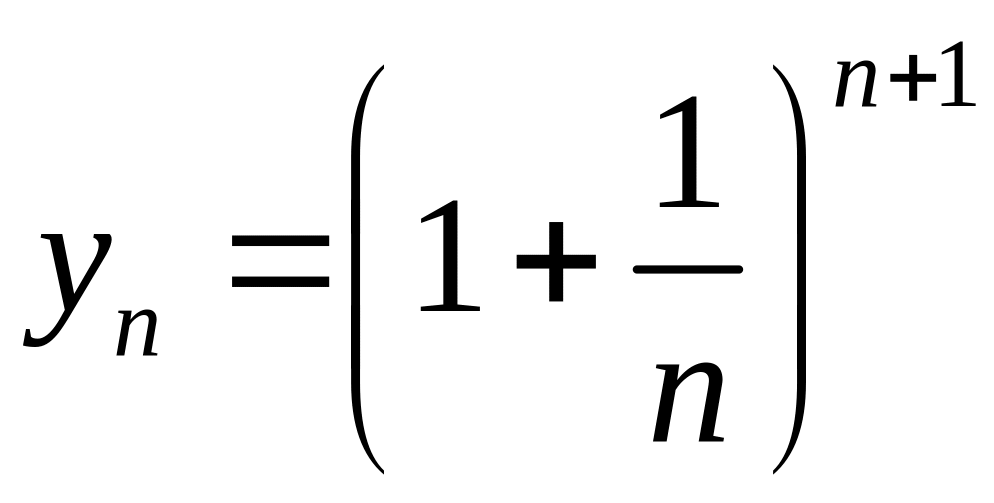. Докажем сначала, что последовательность ограничена снизу.

.

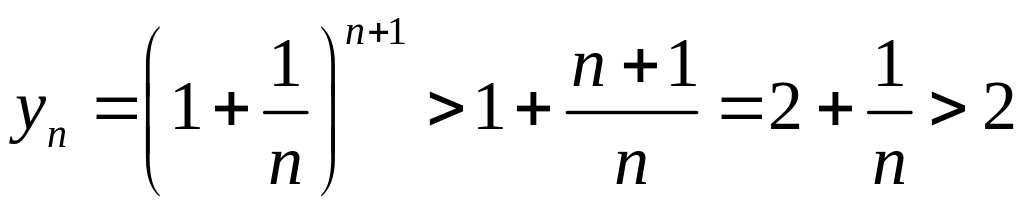Затем докажем ее монотнное убывание

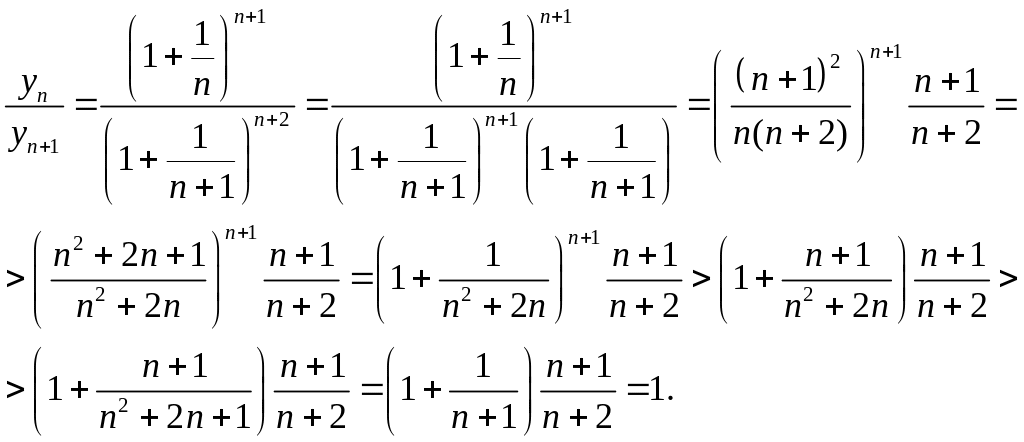
Отсюда следует, что . Тогда существует предел последовательности . Обозначим его через .

Конец примера.

Замечание 14.1. .

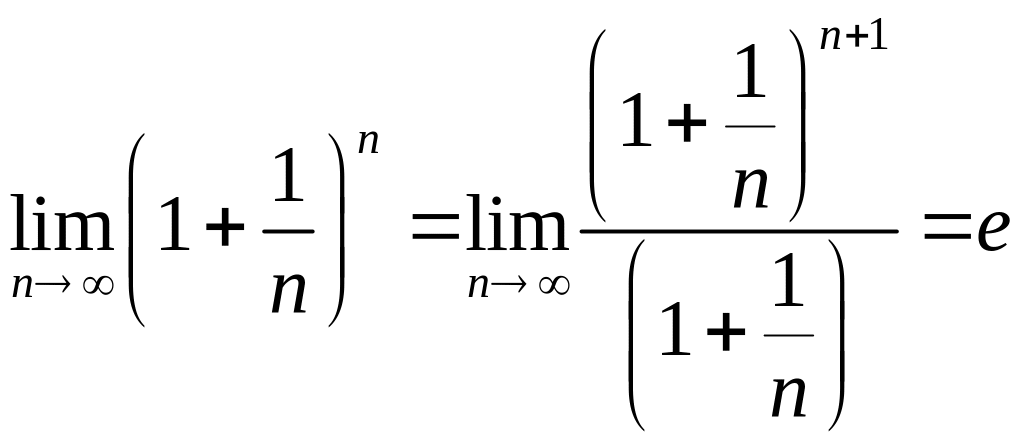Определение 14.7. Числовая последовательность сходится к бесконечности, если для любого существует такое, что для всех справедливо неравенство . В этом случае пишут .

Если заменить неравенство в определении на или , то получим сходимость к или , тогда пишут

.