Лекция № 11. Аналитическая геометрия.

Вопрос 11.1. Прямая на плоскости.

Пусть прямая L лежит в плоскости P. Выберем декартову систему координат на плоскости XY так, чтобы ось X совпадала бы с прямой L. Тогда уравнение прямой L будет иметь вид . Найдем уравнение прямой L в произвольной декартовой системе координат на плоскости P. Рассмотрим вспомогательную лемму.

Лемма 11.1. Пусть на плоскости P заданы две произвольные системы координат CS и . Тогда координаты произвольной точки M плоскости P в системе координат CS и связаны соотношением

, (1)

. (2)

образуют базис соответственно для систем координат CS и (см. рис. 1).

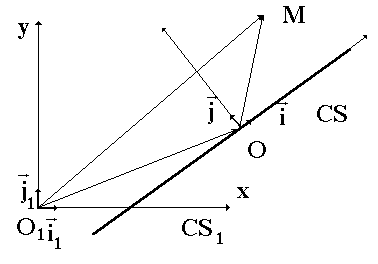
Рис. 1. К доказательству леммы 1.

Разложим вектора первого базиса по векторам второго базиса

, (3)

. (4)

Радиус-векторы точки M в системах координат CS и связаны равенством

(5)

где O и начала координат для CS и . Разложим радиус-векторы по базисным векторам

, (6)

, (7)

. (8)

Тогда, подставляя формулы (6)-(8) в формулу (5), получим

. (9)

С помощью соотношений (3) и (4) преобразуем (9) в равенство

Перенесем все величины в правую часть равенства и сгруппируем слагаемые, тогда получим

Откуда получаем в силу линейной независимости векторов

,

,

что эквивалентно уравнениям (1) и (2).

Конец доказательства.

Теорема 11.1. В любой системе координат прямая L, расположенная в плоскости P, описывается линейным уравнением

. (11)

Доказательство. Пусть CS произвольная система координат. Выберем новую систему координат так, чтобы ось совпала с прямой L. Тогда уравнение прямой L будет . Согласно лемме 11.1, и мы получаем уравнение (11).

Конец доказательства.

Вопрос 11.2. Различные типы уравнений прямой на плоскости.

Рассмотрим теперь различные типы уравнений прямой на плоскости.

1) Общее уравнение прямой l на плоскости.

. (11)

Из вывода уравнения прямой следует, что одновременно не равны 0 (объясните почему). Точка принадлежит прямой L только в том случае, когда ее координаты удовлетворяют уравнению прямой. В зависимости от коэффициентов A, B и C прямая L занимает то или иное положение:

‑ прямая проходит через начало системы координат.

‑ прямая не проходит через начало системы координат.

‑ прямая параллельна оси X.

‑ прямая не параллельна оси X.

‑ прямая параллельна оси Y.

‑ прямая не параллельна оси Y, в этом случае уравнение прямой можно представить в виде , k ‑ коэффициент наклона прямой.

Докажите эти утверждения самостоятельно.