15. Кручение. Крутящие моменты и их эпюра.

Кручение - это такой вид нагружения, когда из шести внутренних силовых факторов в поперечном сечении стержня возникает только один - крутящий момент.

Стержень, работающий на кручение, называют валом.

Кручение возникает при нагружении стержня парами сил, расположенными в плоскостях, перпендикулярных продольной оси.

Момент внутренних сил относительно продольной оси называют крутящим моментом.

При кручении внутренний силовой фактор (крутящий момент) действует в плоскости сечения стержня, в результате чего возникает только касательные напряжения. Касательные напряжения по сечению распределены неравномерно: максимальны на поверхности и уменьшаются до нуля к центру стержня. При этом касательные напряжения зависят не только от площади поперечного сечения, но и от формы.

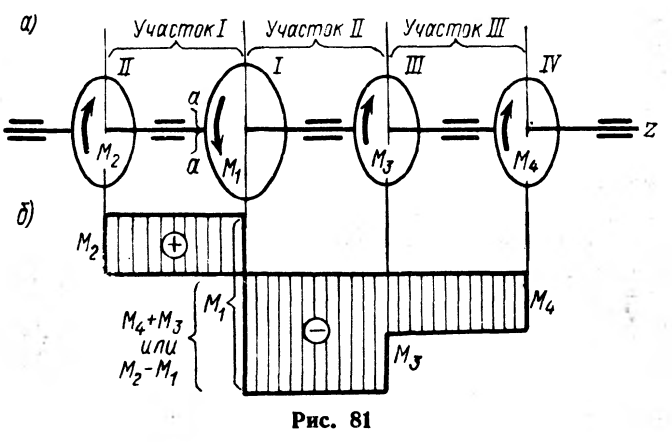
Характер изменения кручения по длине вала наиболее наглядно может быть представлен эпюрой крутящих моментов. Рассмотрим вал, на котором закреплено несколько шкивов. (81 а): шкив 1 получает вращение от двигателя, шкивы 2, 3,4 передают его станкам. Моменты, передаваемые каждым шкивом на вал, вычисляются по формуле (Р- передаваемая мощность, n-частота вращения). Направление момента M₁ противоположно направлению моментов M₂, M₃, M₄. При установившемся движении (равномерном вращении вала), пренебрегая трением в подшипниках, получаем из условия равновесия вала: Крутящий момент изменяется в сечениях вала, передающих внешние моменты от шкивов. Разделим вал на три учаска и определим крутящие моменты в поперечных сечениях.

Крутящий момент в любом поперечном сечении первого участка между шкивами 2 и 1 уравновешивает момент внешней пары M_2­, действующий на левую отсеченную часть При рассмотрении правой части из условяи ее равновесия мы получили бы тот же результат: Аналогично вычисляется крутящий момент в поперечных сечениях на втором участке вала между шкивами 1 и 3 а на третьем участке между шкивами 3 и 4 .

Итак, крутящий момент в каком-либо поперечном сечении вала численно равен алгебраической сумме моментов внешних пар, дейтсвующих на вал в плоскостях, перпендикулярных оси вала, и приложенных по одну сторону от рассматриваемого сечения. Эпюру крутящих моментов строят аналогично эпюре продольных сил, откладывая от горизонтали ординаты, пропорциональные крутящим моментам в поперечных сечениях соответствующих участков вала. Знаки крутящего момента определяются исходя из направления внених моментов. Крутящий момент положителен, когда внешние моменты вращают отсеченную часть по часовой стредке, если смотреть со стороны проведенного сечения. Положительные ориднаты эпюры откладываются вверх, отрицательные вниз от горизонтальной линии (ось эпюры).

16. Напряжения в стержнях круглого поперечного сечения при кручении.

Опыты показывают, что если на поверхности бруса круглого сечения нанести прямоугольную сетку, а на торцевой поверхности нанести радиальные линии (рис.5.5), то после деформации кручение окажется что:

- все образующие поворачиваются на один и тот же угол , а прямоугольники, нанесенные на поверхности, превращаются в параллелограммы;

- торцевые сечения остаются круглыми, плоскими, расстояния между ними не меняются;

- каждое сечение поворачивается относительно другого на некоторый угол , называемый углом закручивания;

- радиальные линии на торцевой поверхности остаются прямыми.

Рассмотрим поперечное сечение вала, расположенное на некотором расстоянии z от торцевого, где Мк=T (рис.5.5). На элементарной площадке dF будет действовать элементарная сила , момент который относительно оси вала равен . Крутящий момент Мк, в сечении равен

.

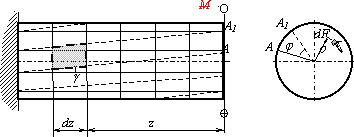
Рис.5.5

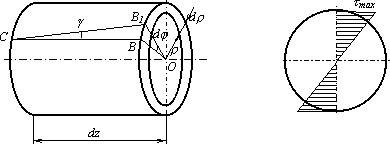
Для того чтобы проинтегрировать это выражение необходимо знать закон распределения напряжений в сечении. Выделим из вала элементарное кольцо длиной dz и толщиной (рис.5.6).

Правый торец элемента повернется относительно левого на угол , образующая СВ повернется на угол и займет положение СВ1. Угол - относительный сдвиг. Из треугольника ОВВ1 найдем:

(рис 5,6 и 5,7)

Из треугольника СВВ1: . Откуда, приравнивая правые части, получим На основании закона Гука при сдвиге: (*) тогда Откуда

Подставим значение в выражение (*) получим: Таким образом, касательные напряжения при кручении прямо пропорциональны расстоянию от центра тяжести сечения до рассматриваемой точки и одинаковы в точках, одинаково удаленных от центра тяжести сечения