5. Растяжение и сжатие стержня. Эпюра продольных сил. Напряжения при растяжении и сжатии.

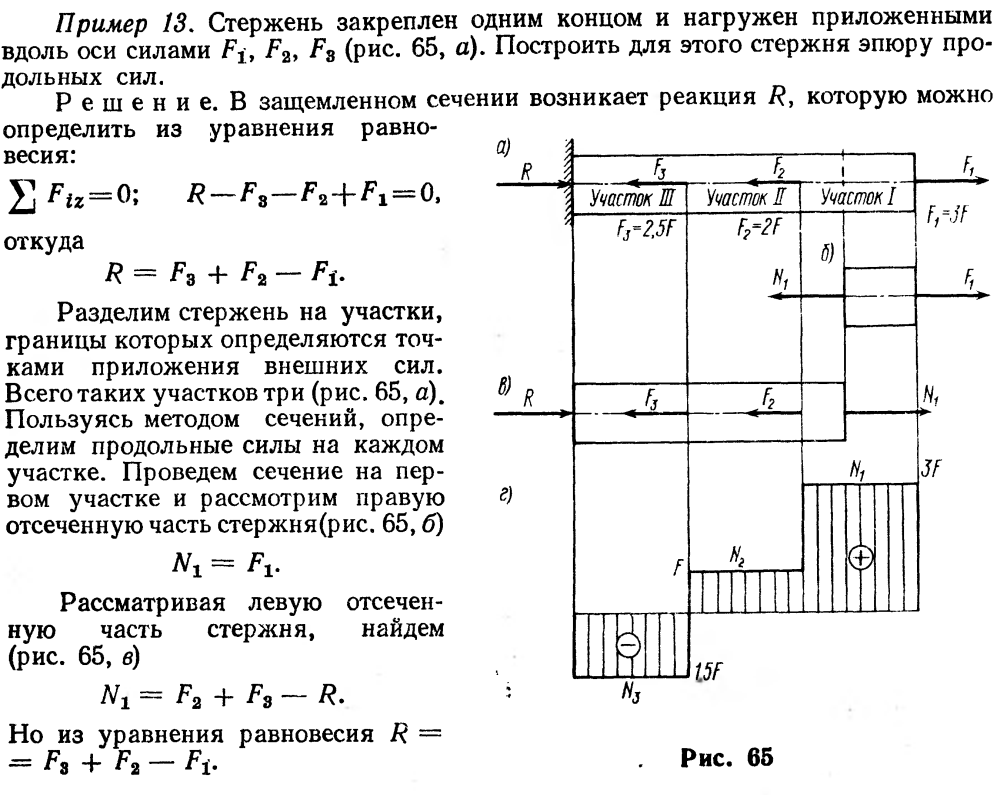
Растяжением (сжатием) называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только продольная сила. Брусья с прямолинейной осью (прямые), работающие на растяжение или сжатие, часто называют стержнями.

Продольная сила в поперечном сечении бруса численно равна алгебраической сумме внешних сил, расположенных по одну сторону сечения.

Растягивающие (направленные от сечения) продольные силы считаются положительными, а сжимающие (к сечению) – отрицательными. Иначе говоря, если равнодействующая вешних сил, приложенных к левой части бруса, направлена налево, а приложенных к правой части – направо, то продольная сила будет положительной, и наоборот.

Эпюра продольных сил – диаграмма, показывающая изменение продольной силы по длине стержня.

При растяжении или сжатии осевыми силами стержней из однородного материала, поперечные сечения, достаточно удаленные от точек приложения внешних сил, остаются плоскими и перемещаются поступательно в направлении деформации (гипотеза плоских сечений). На этом основании можно заключить, что все точки какого-либо поперечного сечения стержня находятся в одинаковых условиях и, следовательно, напряжения распределяются по сечению равномерно. Эти напряжения перпендикулярны поперечному сечению, а значит, являются нормальными напряжениями. где N – продольная сила (сумма), А – площадь.

6. Гипотеза плоских сечений. Закон Гука.

Гипотеза плоских сечений заключается в том, что поперечное сечение бруса, плоское и перпендикулярное продольной оси, после деформации остается плоским и перпендикулярным продольной оси.

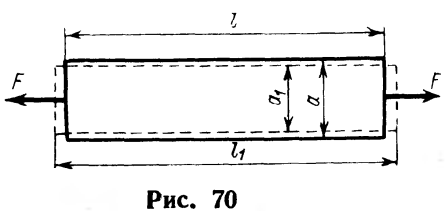
При растяжении стержня его первоначальная длина равно l (рис 70), а длина после растяжения l₁, приращение l=l₁-l является полным изменением стержня и называется удлинением стержня. Отношение удлинения к первоначальной длине стержня =l/l называется продольной деформацией; эта величина определяет удлинение каждой единицы первоначальной длины стержня (проценты или число).

Закон Гука: продольная деформация прямо пропорциональна соответствующему нормальному напряжению. 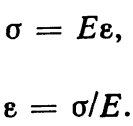Е – модуль продольной упругости – характеризует его жестость, т.е. способность сопротивлятся упругому деформированию. Н/м² (Па).

7. Коэффициент Пуассона. Удлинение стержня при растяжении и сжатии.

Если в формулу закона Гука подставить выражения то получим Произведение , стоящее в знаменателе, называется жестокстью сечения при растяжении и сжатии. Формула читается так: абсолютное удлинение или укорочение прямо пропорционально продольной силе, длине и обратно пропорционально жесткости сечения стержня. Отношение называется жесткостью стержня при растяжении или сжатии.

При растяжении и сжатии изменяются и поперечные размеры стержня. Рассмотрим растянутый стержень (рис 70). Поперечный размер, первоначально равный a, уменьшается до а₁. Изменение поперечного размера а=а-а₁, а поперечная деформация _ равна _=а/а.

Экспериментально установлено, что отношение поперечной деформации _ к продольной деформации  при упругом растяжении (сжатии) для данного материала величина постоянная. Обозначив абсолютное значение данного отношения , получим =|_/|. Следует учитывать, что продольная и поперечная деформация всегда протовоположны по знаку. Иными словами, при растяжении, когда продольный размер стержня увеличивается, его поперечный размер уменьшается,и, наоборот, при сжатии продольный размер уменьшается, а поперечный – увеличивается. Величина  называется коэффициентом поперечной деформации, или коэффициентом Пуассона.