Добавил:

darkl0rd Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Запорожский национальный технический университет

Предмет:

Основы теории колец

Файл:

otksp_STZI_press для диска

.pdf

Скачиваний:

Добавлен:

13.12.2019

Размер:

17.87 Mб

Скачать

☆

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 1819 / 5519 20 21 22 23 24 25 26 27 28 29 30 31 > Следующая >>>

16.До кола, що складається з послідовно сполучених опору R = 8 кОм та індуктивності L = 6 мГн, прикладено напругу u(t) =141cos(106 t +π/ 3) В. Знайти у

колі струм, активну, реактивну і повну потужності.

Відповідь: i(t) =14,1cos(106 t +0,41) мА; 0,8 Вт; 0,6 ВАр; 1 ВА.

17.До послідовного кола (R = 20 Ом, L = 100 мГн і С = 50 мкФ) прикладено напругу u(t) =14,14sin(377t) В. Обчислити комплексні діючі значення струму і на-

пруги на елементах R, L і С, побудувати векторну діаграму.

Відповідь: 0,396e j37,50 А; 7,92e j37,50 В; 14,95e j127,50 В; 21e− j52,50 В.

18. Комплексний опір ділянки кола дорівнює 3 + j5 Ом. Обчислити активну і


реактивну провідності.		Відповідь: G = 0,082 См; B =0,147 См.
19.	Комплексна провідність ділянки кола дорівнює 0,2 − j0,2 См. Обчислити
активний і реактивний опори.		Відповідь: R = 2,5 Ом; X = 2,5 Ом.	U = 30 В і
20.	На ділянці кола задані комплексні діючі значення напруги
струму I = 6 + j0,9 А. Знайти комплексний опір і комплексну провідність кола.
Відповідь: Z = 4,95e− j8,50 Ом; Y = 0,202e j8,50 См.
21.	Щоб визначити параметри котушки індуктивності R, L,		проведене

вимірювання прикладеної напруги (вольтметром) і струму (амперметром) в двох режимах: а) f1 = 0, U1 =100 В, I1 =1А; б) f2 =500 Гц, U2 =100 В, I2 = 0,5 А.. Знайти

параметри котушки, а також показання амперметра при	f3 =1000 Гц, U3 =100 В.
Відповідь: R = 100 Ом; L = 55 мГн; I = 0,277 А.
22. Обчислити коефіцієнт ємнісного зв’язку	для схеми з прикладу 3.9

(рис.3.30, б), якщо величиною паразитної ємності Cп не можна знехтувати (через недостатні розміри екрану).

23. Задані параметри трансформатора: опір 40	Ом та індуктивність 0,05 Гн −
для первинної обмотки, опір 50 Ом та індуктивність	0,05 Гн − для вторинної обмот-
ки; коефіцієнт зв'язку 0,6. Первинна обмотка приєднана до джерела ЕРС 100cos 400t
В, вторинна обмотка − до джерела ЕРС 150cos(400t −300 ) В. Електрорушійні сили
джерел спрямовані до однойменних затискачів трансформатора. Обчислити активні

потужності від кожного з джерел, які йдуть на втрати всередині трансформатора.

Відповідь: 128 Вт; 360 Вт.

L	* М	L	24. Опір взаємної індукції двох од-
1		2 *	накових індуктивно зв'язаних котушок з
Em1		Em2	комплексним опором 10 + j10 Ом кожна
	С		дорівнює	j4 Ом (рис.3.56). Комплексний
			опір ємності дорівнює − j20 Ом, а ЕРС
R1		R2	джерел	становлять Em1 =10 В	і
			Em2 =10e j300 В. Знайти напругу		на
Рисунок 3.56 – Схема кола			ємності.
			Відповідь: 10,95e− j1,30 В.
з індуктивно зв′язаними котушками


Основи теорії кіл, сигналів та процесів в СТЗІ. Ч.1	181

25. Трансформатор, що має дві обмотки на спільному осерді, характеризується такими даними: R1 =100 Ом, L2 =1 Гн, загальний опір вторинної обмотки і наван-

таження 10 кОм, відношення кількості витків N1 / N2 =10, коефіцієнт зв'язку k = 0,5. Обчислити параметри чотириполюсної схеми заміщення (рис.3.41, б).

Відповідь: L1 − M = −0,04 Гн, L2 − M = 0,95 Гн, M = 0,05 Гн. 26.Пояснити поняття: а) ідеальний; б) довершений; в) реальний трансформатор.

27.Пояснити поняття однойменних затискачів індуктивно зв'язаних котушок.

28.Пояснити застосування трансформатора як узгоджувального пристрою.

29.Пояснити поняття коефіцієнта трансформації. Як він обчислюється?

30.Пояснити суть основних методів апроксимації нелінійних характеристик. Як впливає форма характеристики на вибір методу апроксимації?

31.Чим визначається вибір степеня полінома, яким апроксимують ВАХ?

32.Апроксимувати ВАХ нелінійного елемента, задану в табл.3.15, поліномом другого степеня в діапазоні u = −5...0 В. Визначити похибку апроксимації при значенні напруги –1 В.

Таблиця

3.15 – ВАХ нелінійного елемента

u , В

−0,5

−1,0

−1,5

−2,0

−2,5

−3,0

−3,5

−4,0

−4,5

−5,0

i , мА

7,5

6,5

5,5

4,5

3,6

2,7

2,0

1,4

0,75

0,4

0,25

Відповідь: i(u) = 7,5 + 2,37u +0,1865u2 мА; ∆i =3,3% .

33. На

нелінійний

елемент з

ВАХ

i(u) = 20 +5u +0,2u2 мА

діє напруга

u(t) = −5 +5cosω0t В. Знайти постійну складову і амплітуди гармонічних складових

струму через цей елемент.

Відповідь: I0 = 2,5 мА; Im1 =15 мА; Im2 = 2,5мА.

34.Чим відрізняють режими великих і малих коливань у нелінійному колі при синусоїдній дії?

35.Пояснити поняття «кут відсікання». У чому полягає зміст розрахунку нелінійного кола за методом А.І. Берга?

36.Які значення кута відсікання відповідають режимам нелінійного кола А,

АВ, В, С?

37.ВАХ нелінійного елемента апроксимована двома відрізками прямих:

0,	u <Uu ;	Uu	= −6B ; S =5мА/В.
i(u) =
S(u −Uu ), u ≥Uu ;
На вхід подано	напругу u(t) =U0 +Um cos(2π 103t) В. Знайти кут

відсікання, постійну складову і амплітуди першої, другої і третьої гармонічних складових струму через цей елемент, якщо U0 = −10 В, Um =8 В. Побудувати часову

діаграму струму.

Відповідь: θ = 600 ; I0 = 4,4 мА; Im1= 7,8 мА; Im2=5,6 мА; Im3 = 2,8 мА. 38. За яких значень напруги зміщення U0 і кута відсікання θ струм у по-

передній задачі міститиме тільки постійну складову I0 і першу гармоніку Im1 ? Знайти I0 та Im1 . Відповідь: U0 = 2 В; θ =1800 ; I0 = 40 мА; Im1 = 40 мА.

182	Ю.О.Коваль, І.О.Милютченко, А.М.Олейніков та ін.

КОМПЛЕКСНІ ПЕРЕДАТНІ ФУНКЦІЇ ЕЛЕКТРИЧНИХ КІЛ. ЧАСТОТНІ ХАРАКТЕРИСТИКИ

•Поняття і визначення

•Вибірні властивості електричних кіл. Смуга пропускання

•Послідовний коливальний контур. Схеми контуру. Резонансний режим. Вторинні параметри. Резонансні криві

•Комплексні передатні функції і частотні характеристики послідовного контуру. Абсолютна, відносна і узагальнена розстройки

•Вибірність резонансного контуру. Смуга пропускання

•Вплив опорів джерела і навантаження на вибірні властивості послідовного контуру

•Паралельний резонансний контур

•Складні паралельні контури

R L

E C

T	=	1	= 2π LC	Л. Мандельштам

рез		fpез

Дзвоник

У. Томсон

О. Попов


Основи теорії кіл, сигналів та процесів в СТЗІ. Ч.1	183

4 КОМПЛЕКСНІ ПЕРЕДАТНІ ФУНКЦІЇ ЕЛЕКТРИЧНИХ КІЛ. ЧАСТОТНІ ХАРАКТЕРИСТИКИ

4.1 Поняття і визначення

Аналіз усталеного режиму лінійного електричного кола (ЛЕК) при синусоїдній дії показує, що миттєві значення струмів (напруг) також змінюються за синусоїдним законом з частотою дії. При цьому амплітуди і початкові фази струмів (напруг) залежать як від схеми і параметрів кола, так і від амплітуди та початкової фази дії. Щоб визначити відгук лінійного електричного кола на довільну дію, застосовуючи спектральний метод (див. підрозд. 3.1), необхідно багаторазово обчислювати комплексним методом амплітуди і початкові фази гармонік відгуку, спричинені відповідними гармоніками дії. Щоб спростити подібні розрахунки, використовують комплексні передатні функції (КПФ) кіл.

I mвх

I mвих

Щоб визначити КПФ, лінійне електрич-

не коло умовно подають у вигляді двоабо

mвх

Л Е К

mвих

чотириполюсника.

Чотириполюсник

− це

схема з двома парами затискачів (рис.4.1).

Пара затискачів, до яких підведено дію, нази-

вають вхідними,

а затискачі, на яких

Рисунок 4.1 − Позначення

визначається відгук, − вихідними.

кола як чотириполюсника

Комплексні амплітуди напруги U mвх

або струму

I mвх на вході чотириполюсника можна умовно позначити

F m вх

(дія),

а комплексні амплітуди напруги U mвих або струму I mвих на виході –

F m вих

(відгук). Тоді,

комплексна передатна функція кола − це відношення

комплексної амплітуди відгуку до комплексної амплітуди дії:

H (ω) =	F m вих	.	(4.1)
	F m вх

Значення H (ω) не зміниться, якщо комплексні амплітуди дії та відгуку

замінити комплексними діючими значеннями, не використовуючи при цьому в правій частині виразу (4.1) індекс m :

H (ω) =	F вих	.	(4.2)

	F вх

Залежно від того, яка величина (струм або напруга) є дією, а яка − відгуком, КПФ H (ω) має різне фізичне значення і розмірність.

1. Якщо F вх =U вх , F вих =U вих , то H (ω) = HU (ω) = U вих − безрозмірний

U вх

комплексний коефіцієнт передачі за напругою.

184	Ю.О.Коваль, І.О.Милютченко, А.М.Олейніков та ін.

Якщо F вх = I вх ,

F вих = I вих , то

H (ω) = H І (ω) =

I вих

– безрозмірний

I вх

комплексний коефіцієнт передачі за струмом.

U вих

Якщо F вх = I вх ,

F вих =

вих , то

H (ω) = Ζпер(ω) =

– комплексний

I вх

передатний опір.

I вих

Якщо F вх =

вх ,

F вих = I вих , то H (ω) =Y пер(ω) =

– комплексна пе-

U вх

редатна провідність.

Слід зазначити, що загалом Ζпер(ω) ≠1/Y пер(ω) .

Якщо відгук визначають на вхідних затискачах, коло розглядається як

двополюсник і КПФ набуває значення комплексної вхідної функції.

Якщо F вх =

вх ,

F вих = I вх , то H (ω) =Y вх(ω) =

I вх

– комплексна вхідна

вх

провідність.

Якщо F вх = I вх ,

F вих =

вх , то H (ω) = Z вх(ω) =

вх

– комплексний

I вх

вхідний опір.

Комплексну передатну (вхідну) функцію можна подати в показниковій, тригонометричній та алгебраїчній формах запису:

H (ω) = H (ω) e jϕ(ω) = H (ω)e jϕ(ω) =
= H (ω)cosϕ(ω) + jH (ω)sinϕ(ω) = Re[H (ω)]+ j Im[H (ω)],	(4.3)

де H ( jω) = H (ω) ; ϕ(ω) ; Re[H ( jω)]; Im[H ( jω)] − відповідно модуль, ар-

гумент, дійсна і уявна частини комплексної передатної (вхідної) функції.

КПФ лінійного кола залежить не від комплексної амплітуди дії, а від частоти дії, схеми і параметрів кола. Якщо параметри лінійного кола не змінюються, КПФ та її складові залежать тільки від частоти, що підтверджується виразами (4.1) – (4.3).

Залежність від частоти модуля КПФ кола називається амплітудно-

частотною характеристикою (АЧХ).

Залежність від частоти аргумента КПФ кола називається фазо-

частотною характеристикою (ФЧХ).

Із співвідношень (4.1) – (4.3) виходить:

H (ω) = Fm вих = Fвих ; (4.4)

Fm вх Fвх

ϕ(ω) =ϕвих (ω) −ϕвх (ω) .

(4.5)

Вирази (4.4) та (4.5) показують, що АЧХ характеризує частотну залежність відношення амплітуд (діючих значень) відгуку і дії, а ФЧХ – залежність від частоти різниці початкових фаз відгуку і дії. Таке трактування


Основи теорії кіл, сигналів та процесів в СТЗІ. Ч.1	185

використовується пыд час експериментального вимірювання АЧХ і ФЧХ за до-
помогою приладів, працюючих в автоматичному режимі: вольтметрів,
фазометрів і генераторів із змінюваною частотою. При цьому переважно вико-
ристовують не кутову ω, а циклічну частоту							f .
При графічному поданні частотних характеристик електричного кола
АЧХ і ФЧХ, як правило, зображають окремо (рис.4.2, а, б).
H(f )								Im[H ( f )]			f
6						2	f = 0
						2
4
4
2						0						Re[H(f )]
2												Re[H(f )]
0	10	20	30	40	f, МГц	−2		f→			ϕ(f1)
0	10	20	30	40	f, МГц	−2
			a
ϕ(f )						−4				H(f1)
2,8						−4
1,4											f1	f
0						−6					f1
0						−6	−2,4	−1,2		0	1,2	2,4
−1,4									в
−2,8								Re [H(f )]			Im [H(f )]
0	10	20	30	40	f, МГц	2
			б		г	2
					г	0
Рисунок 4.2 – Графіки: а – АЧХ;						−2
б – ФЧХ; в – АФХ; г – дійсної та уявної						−4
	частин КПФ кола					−6 0
						−6 0		10	20	30	40	f, МГц

Поряд з тим, залежність КПФ від частоти можна зобразити єдиним графіком на комплексній площині, де для кожного значення частоти ω або f

по дійсній осі відкладають Re[H (ω)] , а по уявній – Im[H (ω)]. Тому вектор H (ω1) , що відповідає частоті ω1, має довжину H (ω1) і кут ϕ(ω1) . При змінюванні частоти кінець вектора H (ω) описує деяку криву (рис.4.2, в), яку

називають годографом. Таке подання КПФ інакше прийнято називати

амлітудно-фазовою характеристикою (АФХ) кола. Графік АФХ будують при змінюванні частоти ω або f від нуля до нескінченності, позначаючи стрілкою

напрям зростання частоти.

В окремих випадках аналізують залежності дійсної Re[H (ω)] і уявної

186	Ю.О.Коваль, І.О.Милютченко, А.М.Олейніков та ін.

Im[H (ω)] частин КПФ кола від частоти (рис.4.2, г).

Для розрахунку КПФ і частотних характеристик використовують комплексний метод (див. приклади 4.1 – 4.3).

У тих випадках, коли діапазон змінювання АЧХ великий, застосовують логарифмічні одиниці – бели1 (Б), децибели (дБ) або непери2 (Нп), які основані на десяткових логарифмах та безпосередньо використовуються щодо відношення потужностей: A, Б = lg(P2 / P1) ; A, дБ =10 lg(P2 / P1) .

Оскільки потужності пропорційні квадратам діючих значень струмів і напруг, співвідношення для розрахунку АЧХ в цих одиницях мають вигляд:

H (ω), Б=lg(Fвих / Fвх )2 = 2 lg(Fвих / Fвх )= 2 lg(Fmвих / Fmвх );

H (ω),дБ=10 lg(Fвих / Fвх )2 = 20 lg(Fвих / Fвх )= 20 lg(Fmвих / Fmвх ).

У пристроях СТЗІ частіше застосовують децибели, оскільки бел є порівняно великою одиницею: один бел відповідає змінюванню потужності у десять разів, а напруги або струму – в сто разів.

Порівняння графіка АЧХ, побудованого на рис.4.3, а в децибелах, з вихідним графіком (рис.4.2, а) показує, що застосування логарифмічних одиниць призводить до «розтягування» області малих значень і «стиснення» ділянок з максимальними значеннями.

На відміну від децибела одиниця непер базується на натуральному логарифмі стосовно відношення не потужностей, але амплітуд або діючих значень напруг (струмів). Тому для оцінки АЧХ в неперах справедливе співвідношення:

H (ω), Нп=ln (Fmвих / Fmвх )=ln (Fвих / Fвх ).

Використовуючи зв’язок між десятковими та натуральними логарифмами ( ln x = 2,3 lg x ), можна записати вираз для розрахунку АЧХ в неперах за допо-

могою десяткових логарифмів і отримати співвідношення між неперами і децибелами у вигляді:

	Fmвих			Fвих
H (ω), Нп = 2,3 lg		= 2,3 lg			; 1 Нп ≈ 8,7 дБ; 1 дБ ≈ 0,115 Нп.
	F			F

	mвх			вх
Непери застосовують, розраховуючи узгоджені симетричні чотириполюс-
ники, кола з розподіленими параметрами (довгі лінії) та лінії зв’язку.
Слід зазначити, що логарифмічні одиниці безпосередньо застосовують
тільки для безрозмірних АЧХ: H I (ω)			і HU (ω) . Щоб застосувати логарифмічні

одиниці до розмірних АЧХ Z (ω) і Y (ω) , їх необхідно попередньо пронормува-

1 Белл, A. G. Bell (1847–1922) – американський інженер та винахідник. У 1876 р. отримав у США патент на винайдений ним телефон, а у 1877 р. – додатковий патент на його вдосконалення. Оприлюднив роботи з відтворення і запису звуку. З 1897 р. − директор Смітсоніанського інституту в Бостоні.

2 Непер, J. Napier (1550–1617) – шотландський математик. Виклав властивості логарифмів, увів таблиці логарифмів і правила користування.


Основи теорії кіл, сигналів та процесів в СТЗІ. Ч.1	187

ти. Для нормування, як правило, використовують максимальне значення АЧХ, причому нормувати доцільно і безрозмірні АЧХ.

H(f), дБ

а40

80	0	5 10 15 20	25 30 35 40	45 50	f, МГц
	0	5 10 15 20	25 30 35 40	45 50	f, МГц
H(f)
4
б
2
0 0,1		1	10	100	f, МГц
H(f), дБ	(0)	(1)	(2)	(3)	(lg(f / f	п	))
H(f), дБ						п

в40

0,1	1	10	100	f, МГц
(0)	(1)	(2)	(3)	(lg(f / fп ))

Рисунок 4.3 – Побудова АЧХ у логарифмічному масштабі:

а– по осі ординат (у децибелах); б – по осі частот;

в– по осях ординат (у децибелах) і частот

Будуючи графіки АЧХ і ФЧХ у широкому частотному діапазоні, використовують логарифмічні масштаби також по осі частот, на якій відкладають відрізки, пропорційні логарифмам частоти (рис.4.3, б), за допомогою десяткових логарифмів і логарифмів з основою два.

Логарифмічні частотні шкали не мають точки, яка відповідає ω=0 ( f =0 ), оскільки lg 0 → −∞. Тому побудову частотних характеристик почина-

ють зі значення деякої початкової частоти fп (на рис.4.3, б fп = 0,1 МГц).

Щоб градуювати вісь частот, використовують абсолютні значення частоти або безрозмірні відносні величини: декади lg( f / fп) і октави log2 ( f / fп) . На

графіку АЧХ (рис.4.3, б,в) по осі частот у дужках вказані декади.

188	Ю.О.Коваль, І.О.Милютченко, А.М.Олейніков та ін.

АЧХ, зображені у логарифмічному масштабі по осях частот і ординат, називають логарифмічними (рис.4.3, в). Застосування логарифмічного масштабу по осі частот надає частотним характеристикам більшу наочність в області низьких частот. Крім того, суттєве зменшення крутості логарифмічних АЧХ дозволяє застосувати їх кусково-лінійну апроксимацію.

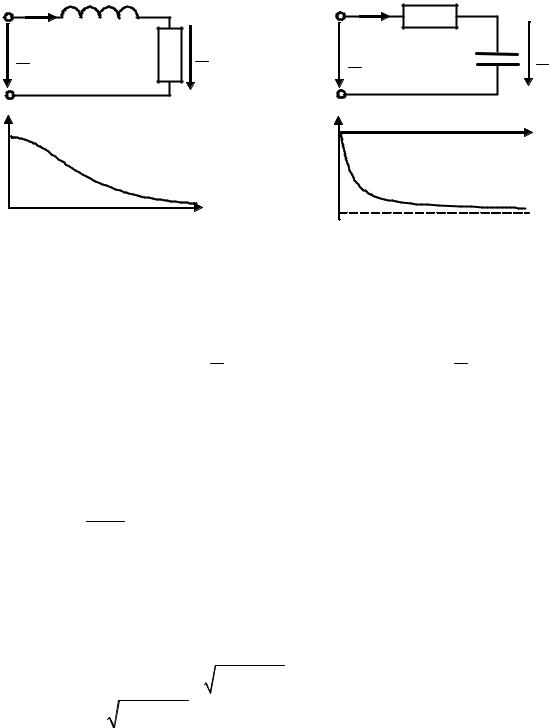
Приклад 4.1. Знайти комплексний коефіцієнт передачі за напругою HU (ω) , АЧХ і ФЧХ для схем (рис.4.4, а, б). Побудувати графіки АЧХ, ФЧХ і АФХ.

а	I	L	R U вих		I	R	C U вих
а	U вх		R U вих	б	U вх		C U вих
	HU (ω)			ϕ(ω)
	HU (ω)			0			ω
	1			0			ω
в				г
	0		ω	−π / 2

Рисунок 4.4 – До прикладу 4.1: а, б – схеми кіл; в – графік АЧХ; г – графік ФЧХ

Розв’язання. Оскільки дані схеми однотипні за структурою і дуальні, визначатимемо HU (ω) разом для двох схем, використовуючи позначення: а – для схеми

(рис.4.4, а); б – для схеми (рис.4.4, б).

Вважаючи відомою напругу U вх , за законом Ома визначимо U вих :

а)

вих=RI=

RU вх

вх

; б)

вих

= I / jωC =

вх

1 +jωL / R

jωC(R +1/ jωC)

R +jωL

+jωRC

Знайдемо HU (ω) :

а)

HU (ω)

вих

U вх

;

U вх

+ jωL / R) U вх

+ jωL / R

+ jωτRL

б)

HU (ω)

вих

U вх

вх

+ jωRC)

вх

1+ jωRC

1+ jωτRC

де τRL = L / R , τRC = RC – величини, які мають розмірність часу і називаються

сталими часу кіл R, L і R, C відповідно.

Оскільки отримані вирази для HU (ω) однотипні, запишемо HU (ω) , АЧХ і

ФЧХ єдиною формулою:

(ω) =

e− jarctg(ωτ)

= H (ω)e jϕU (ω) ,

(4.6)

1+ jωτ

1+(ωτ)2

де

(ω) =1/ 1+(ωτ)2

− рівняння АЧХ; ϕ

(ω) = −arctg(ωτ)

− рівняння

ФЧХ; τ – стала часу, яка дорівнює τRL (τRC ) для кола R, L (R, C).

189

Основи теорії кіл, сигналів та процесів в СТЗІ. Ч.1

Im[HU (ω)]			ω=0	I
0 ω→∞	0,5		1	I	R	L
	ϕU(ω)	2ϕ(ω)	Re[HU (ω)]	U вх		C	U вих
HU (ω)			ω
HU (ω)
Рисунок 4.5 – АФХ (годограф)				Рисунок 4.6 – Схема кола
КПФ кола у прикладі 4.1					у прикладі 4.2

Графіки АЧХ (рис.4.4, в) і ФЧХ (рис.4.4, г) змінюються із зростанням частоти ω монотонно, оскільки розглянуті кола мають один частотно залежний елемент.

Щоб проаналізувати АФХ, перетворимо вираз для HU (ω) :

HU (ω) =

= 0,5 +

0,5 −0,5 jωτ =

+ jωτ

1+ jωτ

0,5 +

0,5 1+

(ωτ)2

− j2arctg(ωτ)

= 0,5 +0,5e

j2ϕ (ω)

(4.7)

1+(ωτ)2

Запис (4.7)

дозволяє подати АФХ (рис.4.5) у вигляді суми двох векторів –

дійсного числа 0,5 і комплексного числа 0,5e

j2ϕU (ω)

, модуль якого є постійним, а ар-

гумент 2ϕU(ω) змінюється залежно від частоти від 0 (при ω = 0 ) до −π (при ω→∞).

Тому годограф АФХ є півколом радіусом 0,5 і координатами центра (0,5; 0).

Вираз

для

HU (ω) , а також

графіки

АЧХ і ФЧХ дозволяють оцінити

можливості практичного застосування досліджуваних кіл.

У діапазоні частот 0 ≤ω<<1/ τ ( ωτ<<1) комплексний коефіцієнт передачі за

напругою HU (ω) ≈1, АЧХ HU ( ω) ≈1, ФЧХ

ϕU (ω) ≈ 0 . Тому вхідні і вихідні ко-

ливання мають однакові амплітуди та початкові фази.

Для

частот

1/ τ<<ω<∞

( ωτ >>1)

коефіцієнт

передачі

за

напругою

HU (ω) ≈1/ jωτ , АЧХ HU (ω) ≈1/ ωτ , ФЧХ ϕU (ω) ≈ −π/ 2 . При цьому миттєві значення вхідної та вихідної напруги можна записати у вигляді: uвх(t)=Umcos(ωt+ψu ) ;

uвих(t) ≈ Uωτm cos(ωt+ψu−π / 2) = Uωτm sin(ωt+ψu ) =τ1 ∫uвх(t)dt .

Отже, за умови ωτ >>1 розглянуті кола з точністю до коефіцієнта 1/ τ виконують операцію інтегрування вхідних коливань і тому називаються інтегрувальними.

Приклад 4.2. Розрахувати комплексний коефіцієнт передачі за напругою HU ( f ) для схеми (рис.4.6). Параметри схеми: R = 5 Ом; L =1,75 мкГн; C = 400пФ.

У діапазоні частот (0…10) МГц побудувати графіки АЧХ, ФЧХ, АФХ для HU ( f ) ,

Re[HU ( f )], Im[H U ( f )].

Розв’язання. Запишемо вираз для комплексного коефіцієнта передачі:

HU (ω) =

U вих

вх

(1 −ω2LC) + jωRC

U вх

(R + jωL +1/ jωC)

вх

jωC

190

Ю.О.Коваль, І.О.Милютченко, А.М.Олейніков та ін.

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 1819 / 5519 20 21 22 23 24 25 26 27 28 29 30 31 > Следующая >>>