Метод трапеций
Повторим ту же самую методику получения итерационной формулы для линейной аппроксимирующей функции. В этом случае между точками f(a) и f(b) проводим линейную зависимость, а уравнение аппроксимирующей прямой имеет вид:
(39)
Площадь под аппроксимирующей прямой – это площадь трапеции (рис. 5), следовательно:
(40)
f(x)
f(b)
f(a)
x a
b
Рис. 5. Аппроксимирующая линия на интервале интегрирования
Интегрирование аппроксимирующей функции приводит к такому же результату:
(41)
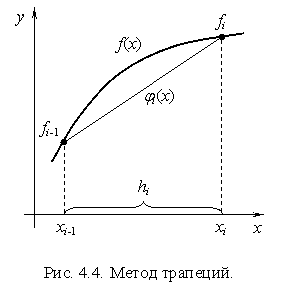
Теперь представим, что разбили интервал [a, b] на N малых интервалов, аналогично рис. 4, б и выделим отдельный малый интервал (рис. 6).
Y(x))
Рис. 6. Метод трапеций
Из рисунка 6 следует, что расчетную формулу метода трапеций можно представить следующим образом:
(42)
В программе MathCad реализованы методы прямоугольников и трапеций для вычисления определенного интеграла с заданным количеством интервалов разбиения.
Программа 16
Чтобы оценить, с какой точностью рассчитано значение интеграла, надо записать в тетрадь для отчетов полученное значение интеграла как SN, затем увеличить число интервалов N в 2 раза и записать полученное значение интеграла как S2N. Точность вычисления равна разности по абсолютной величине S2N – SN.
По приведенной выше методике можно вывести формулы для полиномов более высоких порядков, чем нулевой и первой степени, однако как геометрическая, так и интегральная форма вывода этих уравнений становятся слишком громоздкими. Более простым способом вывода уравнений является использование квадратурных формул Котеса.
Численное интегрирование с помощью квадратурных формул
Общий вид квадратурной формулы Котеса при постоянном шаге интегрирования можно представить уравнением:
,
(43)
где Ai и m – числа Котеса. Значения чисел Котеса зависят от степени аппроксимирующего полинома (n). Причем их значения получены таким образом, чтобы квадратурная формула была точной, а не приближенной для всех вырожденных полиномов типа у = х0, у = х, у = х2, у = х3,..., у = хn, если сама y(x) является полиномом степени n. Для аппроксимирующих полиномов меньше шестой степени числа Котеса приведены в таблице 6.
Таблица 6
n |
M |
A0 |
A1 |
A2 |
A3 |
A4 |
A5 |
0 |
1 |
1 |
метод прямоугольников |
||||
1 |
2 |
1 |
1 |
метод трапеций |
|||
2 |
6 |
1 |
4 |
1 |
метод парабол Симпcона |
||
3 |
8 |
1 |
3 |
3 |
1 |
полином третьей степени |
|
4 |
90 |
7 |
32 |
12 |
32 |
7 |
|
5 |
288 |
19 |
75 |
50 |
50 |
75 |
19 |
6 |
840 |
41 |
216 |
27 |
272 |
27 |
216 |
При подстановке чисел Аi и N из таблицы 6 в уравнение при n = 0 и n = 1 получаются формулы интегрирования методами прямоугольников и трапеций, выведенные нами ранее (36) и (40). При n = 2 можно получить формулы метода Симпсона (метод парабол).