§ 2. Статистические игры без эксперимента

2.1. Представление статистической игры без эксперимента в виде s - игры

Свяжем с каждой из чистых стратегий статистика точку в - мерном пространстве, координатами которой будут потери статистика при различных стратегиях природы . Например, для задачи о технологической линии этими точками будут точки , и . И выпуклая оболочка множества точек , и дает область всех возможных стратегий статистика: как чистых - , и , так и смешанных - отрезков вида , и :

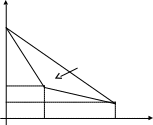
5

3

2

0 1 3

Р ис. 3.1

При выборе своей стратегии игрок может руководствоваться различными принципами оптимальности. При этом среди статистиков не существует единого мнения о том, какой из принципов необходимо применять в каждом конкретном случае. Однако можно прийти к единому мнению о том, чего не надо делать. Для этого вводится понятие допустимых стратегий, аналогично понятию доминирующих стратегий в стратегических играх.

2.2. Допустимые стратегии в статистических играх

Рассмотрим некоторую смешанную стратегию . Тогда возможны два случая:

1. Нельзя найти стратегию 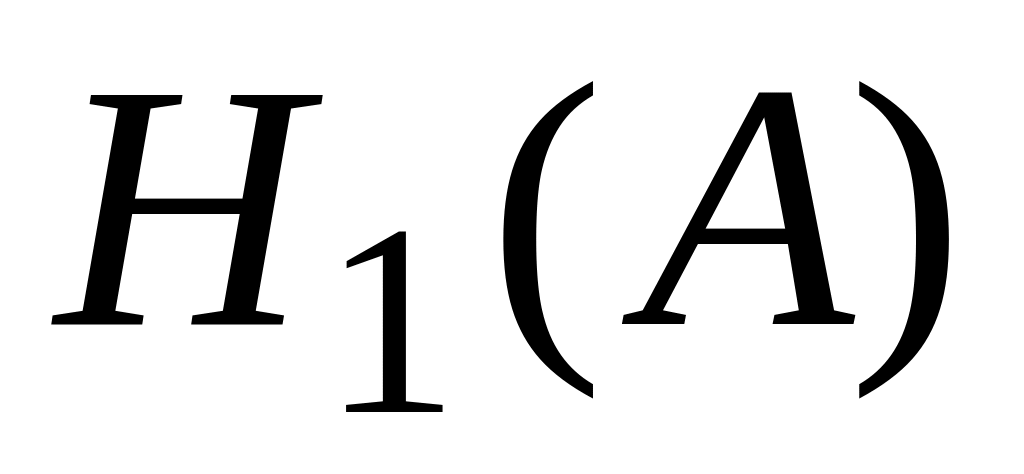лучшую, чем . Это означает, что не существует такой стратегии , для которой справедливо неравенство:

, (3.6)

при всех , , хотя для некоторых это неравенство может и выполняться. В этом случае стратегия называется допустимой..

2. Существует стратегия лучше, чем . Это означает, что неравенство (6) выполняется при всех . В этом случае стратегия называется недопустимой и ее следует исключить из рассмотрения в пользу стратегии .

Допустимые стратегии удобно рассмотреть в терминах - игры, при которой стратегии статистика определяются в виде точек, лежащих на выпуклой оболочке области , а потери статистика определяются координатами соответствующих точек выпуклой оболочки.

Продемонстрируем метод нахождения допустимых стратегий для случая, когда множество состояний природы состоит только из двух элементов и :

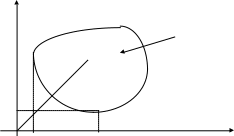
0

Рис. 3.2

Рассмотрим стратегию (точку), расположенную внутри области . Эта стратегия не является допустимой, так как координаты (потери) всех точек, лежащих на отрезке , имеют меньшие значения, то есть представляют явно лучшие решения. Поэтому все «внутренние» стратегии вида можно исключить в пользу стратегии вида , лежащей на границе области .

Следовательно, можно сделать вывод о том, что все множество допустимых стратегий статистика представляет (геометрически) дугу границы области .

№ 3.3. Найти функции потерь для допустимых решений в задаче о технологической линии.

Решение. Левая нижняя граница допустимых решений (см. рис.3.1) состоит из отрезков и , каждый из которых представляет собой смешанную стратегию.

Введем параметр . Тогда параметрическое уравнение отрезка будет иметь вид:

,

и это определяет смешанную стратегию:

.

Спроектировав отрезок на оси координат, получим следующие выражения для функции потерь:

,

.

Аналогично для отрезка с уравнением:

,

получим смешанную стратегию

,

и функции потерь

,

.