1.3. Пространство стратегий статистика. Функция потерь
Задача статистика в игре состоит в том, чтобы принять некоторое решение, или выполнить какое-либо действие из совокупности решений или действий.
Обозначим
возможные действия статистика через
.
Каждое из этих действий является чистой
стратегией статистика, а множество
является пространством чистых стратегий
статистика.
Статистик
должен уметь оценивать каждое из своих
действий. Для этого он допускает, что
совершая действие
,
он может потерпеть убыток
,
зависящий от неизвестного состояния
природы
.
Функция
называется функцией
потерь и
должна быть определена заранее для
всевозможных комбинаций
.
То есть функция потерь задается на
прямом произведении множеств
.
Ее можно определить или аналитически
или в виде матрицы потерь:
,
(3.1)
где
.
Знание такой функции потерь может позволить статистику предпринять такие действия, которые являются наилучшими в условиях имеющейся у него информации о возможных состояниях природы.
Статистику
обычно бывает известно априорное
распределение вероятностей
состояний природы, поэтому он может
определить средние потери, которые он
понесет, выполняя действие (выбирая
стратегию)
:
.
(3.2)
Тогда
наилучшим для статистика действием
будет так называемое байесовское
действие
(решение)
при котором его средние потери будут
минимальны:
.
(3.3)
Статистик может не ограничиваться использованием только одной чистой стратегии, а применить так называемую смешанную стратегию, представляющую «смесь» чистых стратегий в соответствии с некоторым вероятностным законом распределения:
.
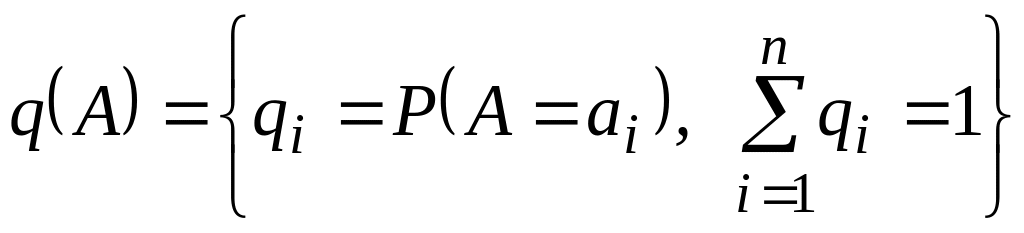В
общем случае статистик располагает
набором смешанных стратегий
,
называемых пространством
смешанных стратегий статистика.
Если
статистик применяет некоторую смешанную
стратегию
,
а природа - смешанную стратегию
,
то средние потери статистика будут
равны:
.
(3.4)
И
задача статистика заключается в выборе
такой смешанной стратегии
,
которая бы минимизировала средние
потери (3.4):
.
(3.5)
где
.
Отметим, что здесь мы рассмотрели простую задачу определения наилучшей стратегии статистика на основе только имеющейся априорной информации о состояниях природы, не делая попыток уточнения своих знаний о действительном состоянии природы путем проведения эксперимента.
Такие статистические игры называются еще статистическими играми без эксперимента.
1.4. Примеры статистических игр
№ 3.1.
(Задача о
замене оборудования). Установленное на
предприятии сложное и дорогое оборудование
после нескольких лет работы может
оказаться в одном из трех состояний:
- оборудование вполне работоспособно
и требует лишь небольшого текущего
ремонта;
- оборудование работоспособно, но
некоторые детали значительно износились
и требуют серьезного ремонта или даже
замены;
- дальнейшая эксплуатация оборудования
невозможна.
Прошлый опыт эксплуатации аналогичного оборудования показывает, что в 20% случаях оно может находиться в состоянии , в 50% случаях - в состоянии , и в 30% - в состоянии .
Для
предприятия возможны три различных
варианта действия:
- оставить оборудование в работе еще на
один год, проведя незначительный ремонт
своими силами;
- провести капитальный ремонт оборудования
с вызовом специальной бригады ремонтников;
- заменить оборудование новым.
Требуется найти байесовское оптимальное решение действий предприятия при следующей матрице потерь:
.
Решение. Вычислим средние потери предприятия:
,
,
.
Тогда байесовское решение дает нам стратегия , так как
.
Ответ: .
№ 3.2. (Задача о технологической линии). На технологическую линию может поступить сырье с малым и с большим количеством примесей. Известно, что в среднем поступает 60% сырья первого вида и 40% сырья второго вида. Для использования различных видов сырья предусмотрены три режима работы технологической линии: , и . Потери, отражающие качество выпускаемой продукции и расходы сырья, в зависимости от качества сырья и режима работы технологической линии, имеют вид:
.
Требуется найти байесовское оптимальное решение.
Решение. Вычислим средние потери:
,
,
.
Тогда оптимальной является чистая стратегия , так как
.
Ответ: .