12. Бесконечно малые последовательности и их свойства

{x_n} – бесконечно малая последовательность ⇔ lim _{n ⟶ ∞} х _n = 0 ⇔ ∀ ε > 0 ∃ N(ε): ∀ n ≥ N |х _n| < ε

Свойства бесконечно малых последовательностей:

{x_n} и {у_n} – бесконечно малые последовательности

• {x_n±у_n} – бесконечно малая

• ∀ α ∈ R {α*x_n} – бесконечно малая

• {x_n*у_n} – бесконечно малая

• {у_n} – ограниченная, тогда {x_n*у_n} – бесконечно малая

ДОКАЗАТЕЛЬСТВО:

lim _{n ⟶ ∞} x_n = 0 ⇔ ∀ ε’ > 0 ∃ N(ε’) ∀ n ≥ N | x_n | < ε {у_n} – ограниченная ⇔ ∃ М > 0: ∀ n ∈ N | у_n | < М

Тогда ∀ n ≥ N, |x_n*у_n| = | x_n |*| у_n | < М*ε’ Следовательно, ∀ ε > 0 (ε’ = ε / М) ∃ N (ε’) : ∀ n ≥ N |x_n*у_n| < ε - что и требовалось доказать

• {1/x_n} – бесконечно большая

13. Монотонные последовательности. Теорема Вейерштрасса( о существовании предела у монотонной последовательности)

{x_n} – монотонно возрастающая, если х _{n +1} ≥ х _n

{x_n} – монотонно убывающая, если х _{n +1} ≤ х _n

{x_n} – строго монотонно возрастающая, если х _{n +1} > х _n

{x_n} – строго монотонно убывающая, если х _{n +1} < х _n

ТЕОРЕМА ВЕЙЕРШТРАССА:

1. Если {x_n} – монотонно возрастающая и ограничена сверху, то lim _{n ⟶ ∞} x_n = sup {x_n}

2. Если {x_n} – монотонно возрастающая и не ограничена сверху, то lim _{n ⟶ ∞} x_n = +∞

3. Если {x_n} – монотонно убывающая и ограничена снизу, то lim _{n ⟶∞} x_n = inf {x_n}

4. Если {x_n} - монотонно убывающая и не ограничена снизу, то lim _{n ⟶∞} x_n = -∞

ДОКАЗАТЕЛЬСТВО:

1. {x_n} - ограничена сверху ⇔ ∃ sup {x_n} = a ⇔ ∀ x_n: x_n ≤ а, ∀ ε > 0 х _N > а – ε. {x_n} - монотонно возрастающая ⇔ х _{n +1} ≥ х _n ∀ n ≥ N х _n ≥ х_N > а-ε х _n < а ⇒ х _n ∈ (а-ε, а ] ∀ ε > 0 ∃ N (ε) ∀ n ≥ N х _n ∈ (а-ε, а] ⇒ lim _{n ⟶ ∞} х _n = а-0 – доказано

2. {x_n} - не ограничена сверху ⇔ ∀ b ∈ R ∃N(b) ∀ n ≥ N х _n > b. Пусть b = 1/ε. ∀ ε > 0 (b = 1/ε) ∃N(b) ∀ n ≥ N х _n > 1/ε ⇒ lim _{n ⟶ ∞} х _n = +∞ - доказано

3. {x_n} - ограничена снизу ⇔ ∃ inf {x_n} = a ⇔ ∀ х _n : х _n ≥ а, ∀ ε > 0 ∃ х_N < а+ε {x_n} - монотонно убывающая ⇔ х _n+1 ≤ х _n ∀ n ≥ N х _n ≤ х _N <а+ε , х _n ≥ а ⇒ х _n ∈ [а, а+ε) ∀ ε > 0 ∃ N(ε) ∀ n ≥ N х _n ∈ [а, а+ε) ⇒ lim _{n ⟶ ∞} х _n = а+0 – доказано.

4. {x_n} - не ограничена снизу ⇔ ∀ b ∈ R ∃N(b): ∀ n ≥ N х _n < b. Пусть b = -1/ε. ∀ ε > 0 (b = -1/ε) ∃N(b): ∀ n ≥ N х _n < -1/ε ⇔ lim _{n ⟶ ∞} х _n = -∞ - доказано.

14. Определение числа «е»

      (1) Из данного равенства (1) следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число  убывает, поэтому величины  возрастают. Поэтому последовательность  — возрастающая, при этом      (2). Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство Т.к. k!≥2^k-1 то 1/k! ≤ 1/2^k-1 . Сумму в скобке найдём по формуле суммы членов геометрической прогрессии: 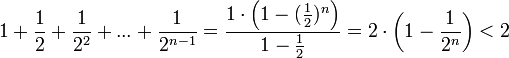. Поэтому        (3). Итак, последовательность ограничена сверху, при этом  выполняются неравенства (2) и (3):    . Следовательно, на основании теоремы Вейерштрасса (критерий сходимости последовательности) последовательность  монотонно возрастает и ограниченна, значит имеет предел, обозначаемый буквой e. Т.е.