Способы вычисления определителей:

1. Определитель можно вычислить, используя непосредственно его определение. Этим способом удобно вычислять определители второго и третьего порядка.

2. Определитель можно вычислить с помощью его разложения по элементам строки или столбца.

3. Определитель можно вычислить способом приведения к треугольному виду. Чтобы получить треугольный определитель, нужно к какой-либо строке (или столбцу) заданного определителя прибавлять соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, до тех пор, пока не придем к определителю треугольного вида.

Пример. Вычислить определитель матрицы по правилу треугольников А =

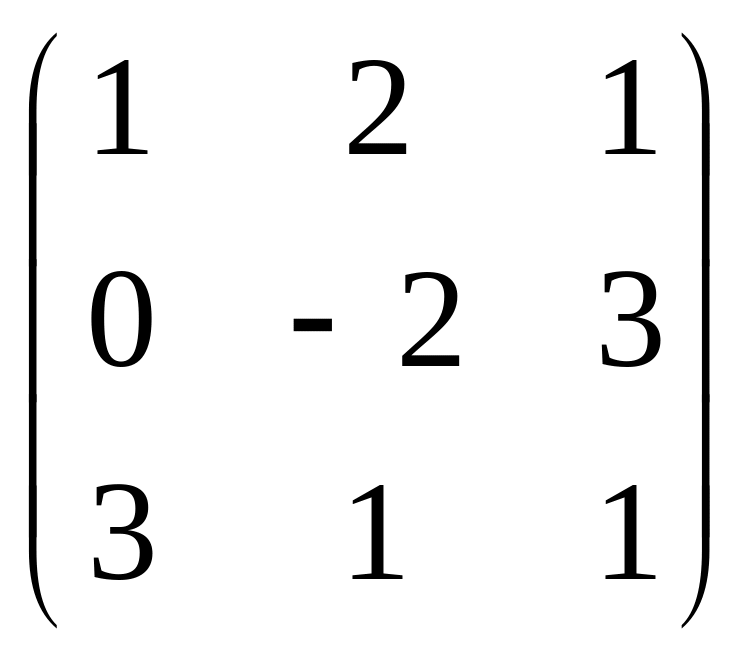
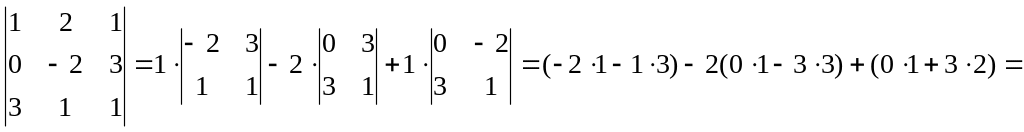
= -5 + 18 + 6 = 19.

Пример. Вычислить определитель с помощью его разложения по элементам первой строки.

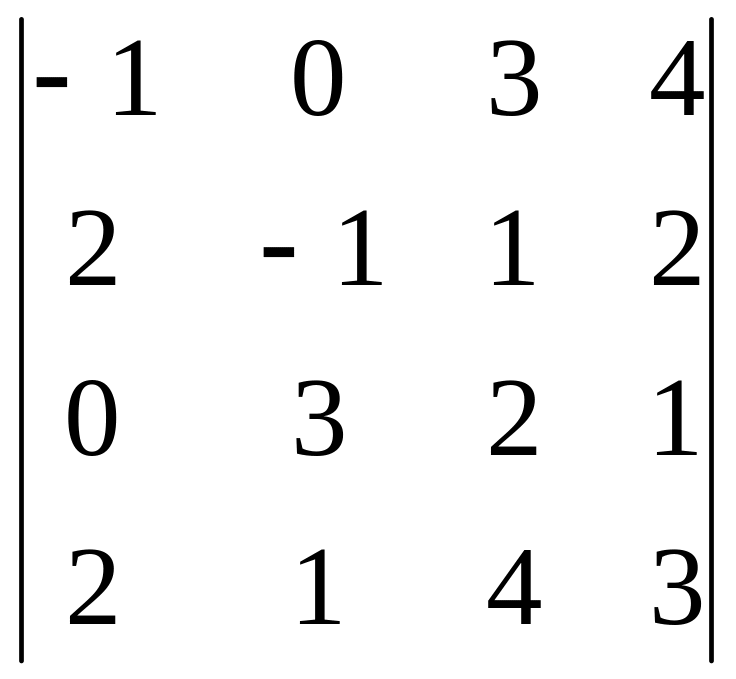= -1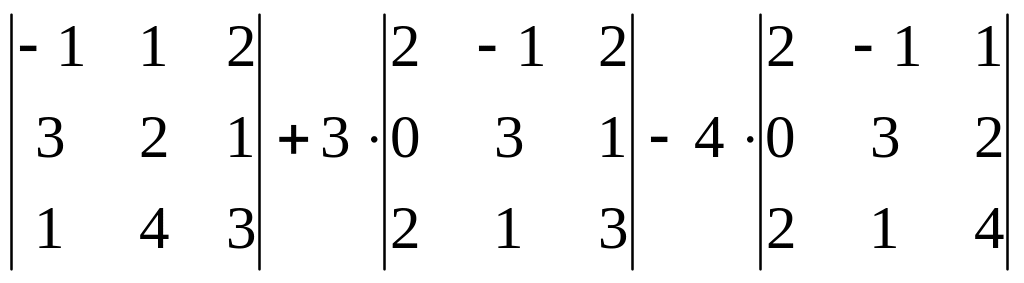

Значение определителя: -1·10 + 3·2 – 4·10 = -44.

Практическое занятие №2

Наименование занятия: Нахождение обратной матрицы. Вычисление ранга матрицы.

Цель занятия: Научиться находить обратные матрицы, вычислять ранг матриц.

Подготовка к занятию: Повторить теоретический материал по теме «Матрицы и определители».

Литература:

1. Григорьев В.П., Дубинский Ю.А. «Элементы высшей математики», 2008г.

Задание на занятие:

1. Найти матрицы, обратные заданным. Проверить результат.

1. ;

2. ;

3. ;

4. ;

5. 

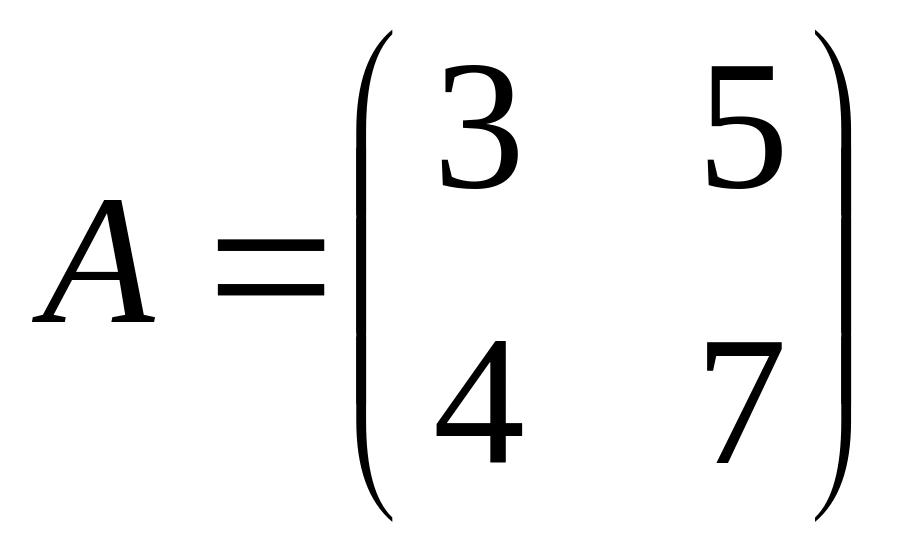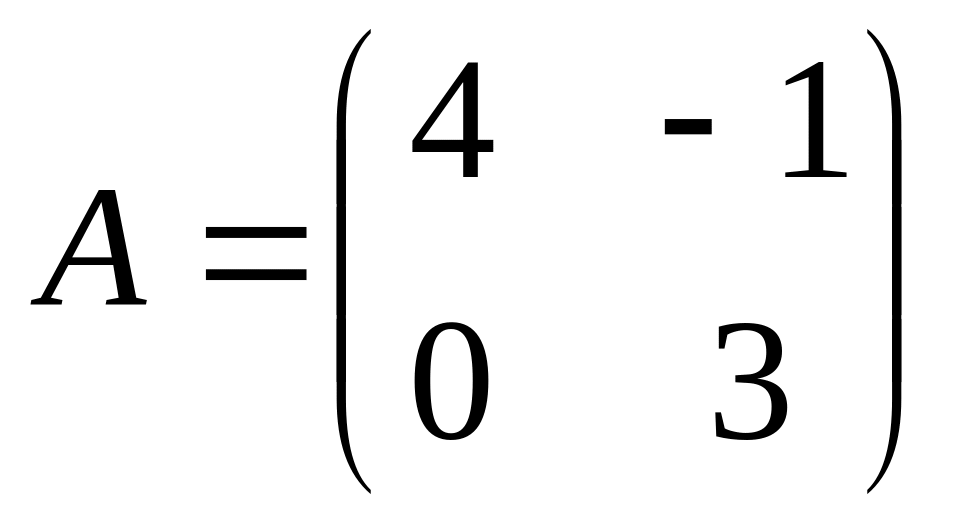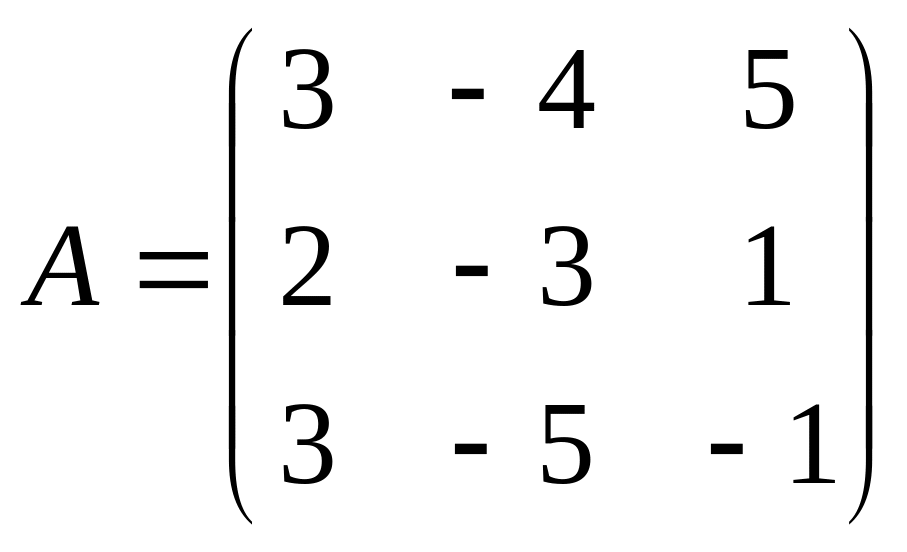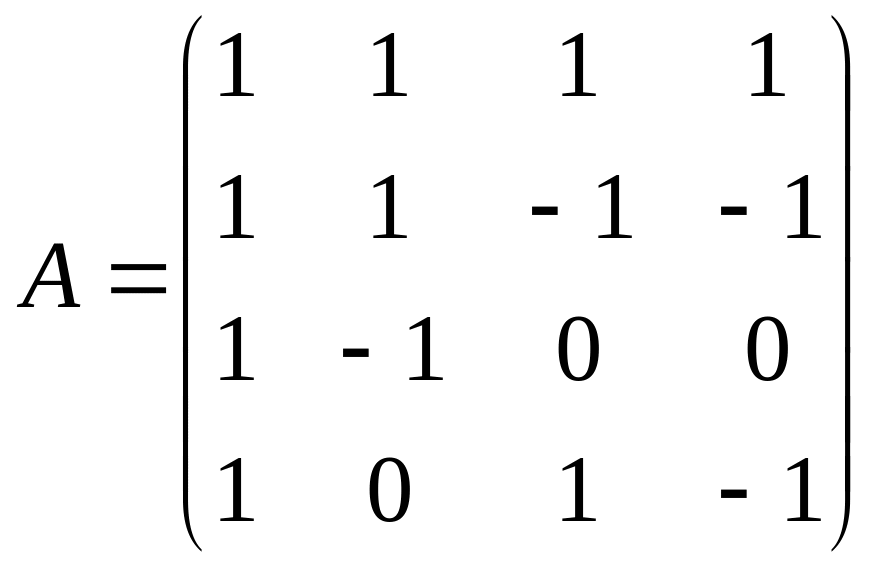
2. Найти ранг матриц.

1. ;

2. 

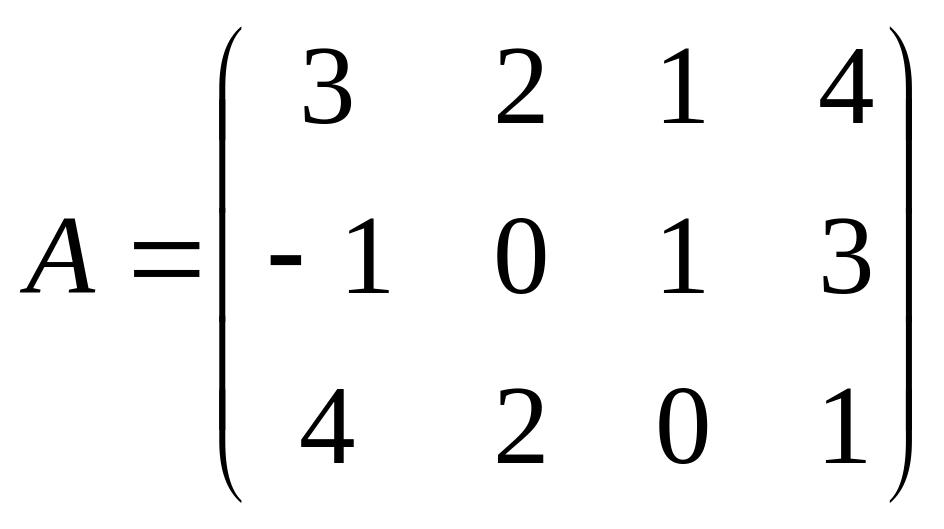Порядок проведения занятия:

1. Получить допуск к работе

2. Выполнить задания

3. Ответить на контрольные вопросы.

Содержание отчета:

1. Наименование, цель занятия, задание;

2. Выполненное задание;

3. Ответы на контрольные вопросы.

Контрольные вопросы для зачета:

1. Какая матрица называется вырожденной, невырожденной?

2. Какая матрица называется обратной по отношению к заданной матрице А?

3. Каково условие существования обратной матрицы?

4. Каков порядок вычисления обратной матрицы?

5. Как найти ранг матрицы?

ПРИЛОЖЕНИЕ

Обратная матрица

Квадратная матрица А называется невырожденной, если ее определитель отличен от нуля. В противном случае матрица А называется вырожденной.

Если А – квадратная матрица, то обратной по отношению к А называется матрица, которая при умножении на матрицу А (как слева, так и справа) дает единичную матрицу. Обратная матрица обозначается символом .

Если А – невырожденная матрица, то для нее существует обратная матрица , которая вычисляется по формуле

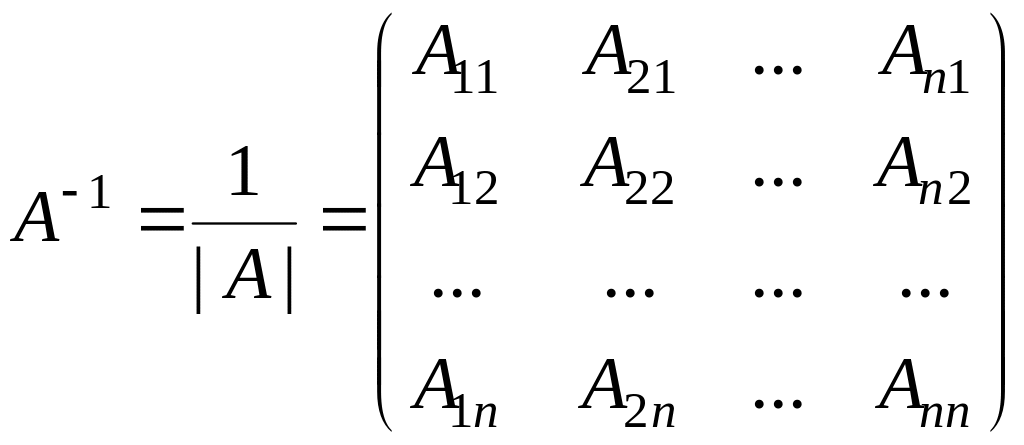, где – алгебраическое дополнение элемента .

Пример. Дана матрица А = , найти А^-1.

Найдем определитель матрицы. = 4 – 6 = – 2 ≠ 0, следовательно, для этой матрицы существует обратная. Найдем алгебраические дополнения к элементам матрицы:

А₁₁ = 4; А₁₂ = – 3; А₂₁ = – 2; А₂₂ = 1

Таким образом, .

Ранг матрицы

Минором порядка матрицы (соответствующим выбранным строкам и столбцам) называется определитель порядка , образованный элементами, стоящими на пересечении выбранных строк и столбцов.

В матрице размеров минор порядка называется базисным, если он отличен от нуля, а все миноры порядка равны нулю или миноров порядка вообще нет, т.е. совпадает с меньшим из чисел m или n.

Рангом матрицы называется порядок базисного минора, или, иначе, самый большой порядок, для которого существуют отличные от нуля миноры.

Вычисление ранга матрицы

Идея практического метода вычисления ранга матрицы заключается в том, что с помощью элементарных преобразований данную матрицу приводят к треугольному виду. Тогда ранг матрицы будет равен числу ненулевых строк в полученной матрице.

Элементарными преобразованиями называют следующие преобразования матриц:

1. Умножение или деление строки на число, отличное от нуля;

2. Сложение и вычитание строк;

3. Перестановку строк;

4. Вычеркивание (удаление) одной из одинаковых строк (столбцов);

5. Транспонирование

Те же операции, применяемые для столбцов, также являются элементарными преобразованиями.

Пример: Определить ранг матрицы.

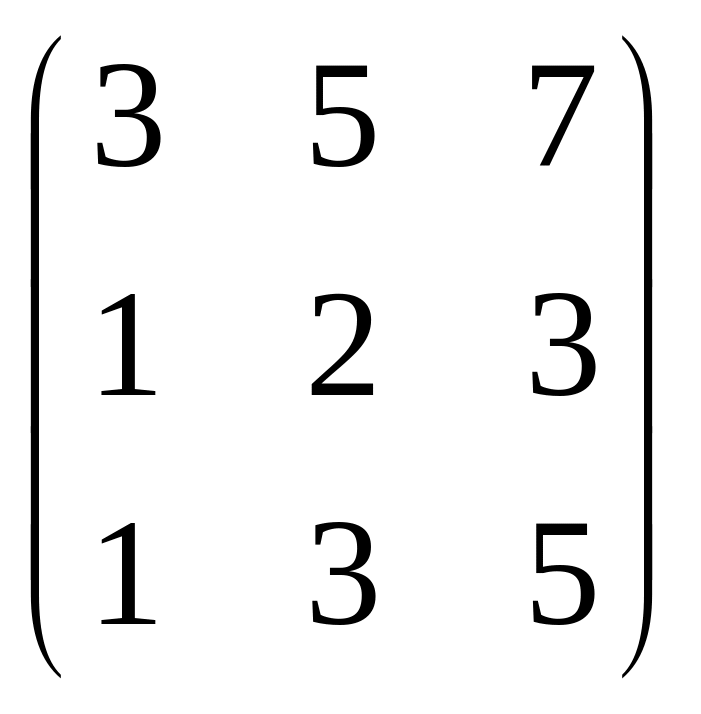
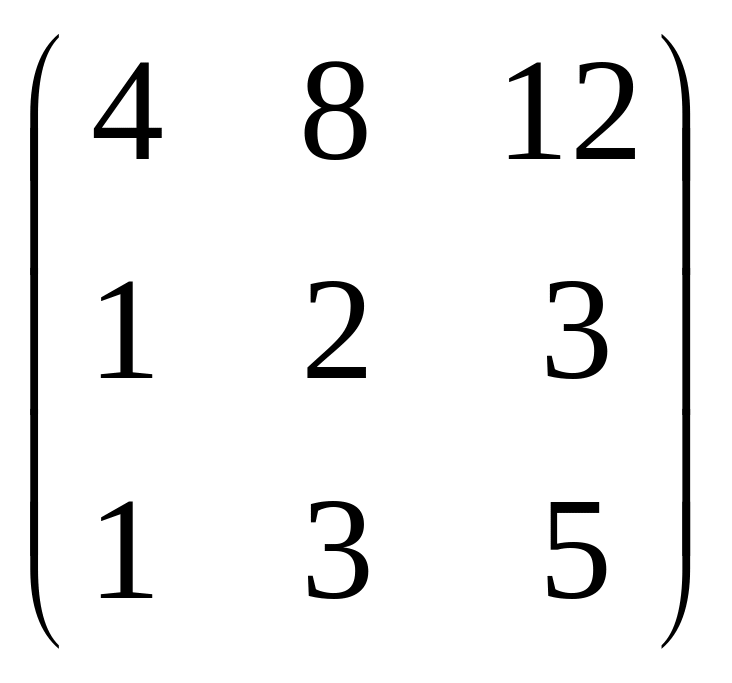
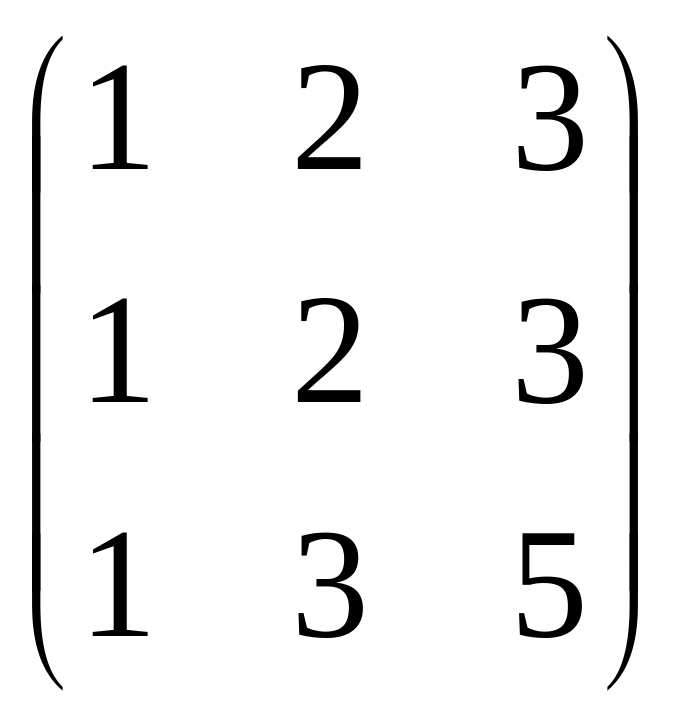
   , Rg = 2.

Если с помощью элементарных преобразований не удается найти матрицу, эквивалентную исходной, но меньшего размера, то нахождение ранга матрицы следует начинать с вычисления миноров наивысшего возможного порядка. В вышеприведенном примере – это миноры порядка 3. Если хотя бы один из них не равен нулю, то ранг матрицы равен порядку этого минора.