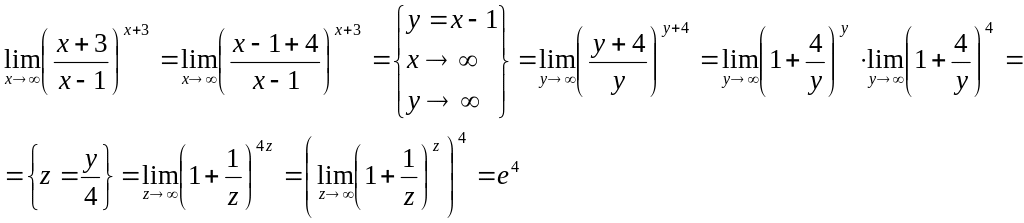- •Практическое занятие №1
- •Вычислить определитель .
- •Вычислить определитель .
- •Действия с матрицами
- •Определители
- •Способы вычисления определителей:
- •Практическое занятие №2
- •Обратная матрица
- •Ранг матрицы
- •Практическое занятие №3
- •Матричный метод решения систем линейных уравнений
- •Метод Крамера для решения систем линейных уравнений
- •Практическое занятие №4
- •Рассмотрим произвольную систему линейных уравнений. Система m уравнений с n неизвестными в общем виде записывается следующим образом:
- •Метод Гаусса
- •Практическое занятие №5
- •Григорьев в.П., Дубинский ю.А. «Элементы высшей математики», 2008г.
- •Дадаян а.А. «Математика», 2004г.
- •Действия над векторами
- •Координаты вектора
- •Действия над векторами, заданными своими координатами
- •Скалярное произведение векторов в координатной форме
- •Практическое занятие №6
- •Григорьев в.П., Дубинский ю.А. «Элементы высшей математики», 2008г.
- •Дадаян а.А. «Математика», 2004г.
- •Уравнение прямой по точке и нормальному вектору
- •Уравнение прямой по точке и направляющему вектору
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой по точке и угловому коэффициенту
- •Уравнение прямой в отрезках
- •Практическое занятие №7
- •Григорьев в.П., Дубинский ю.А. «Элементы высшей математики», 2008г.
- •Дадаян а.А. «Математика», 2004г.
- •Практическое занятие №8
- •Григорьев в.П., Дубинский ю.А. «Элементы высшей математики», 2008г.
- •Действия с комплексными числами в алгебраической форме
- •Геометрическая форма комплексного числа
- •Практическое занятие №9
- •Григорьев в.П., Дубинский ю.А. «Элементы высшей математики», 2008г.
- •Действия с комплексными числами в тригонометрической и показательной формах
- •Практическое занятие №10
- •Основные теоремы о пределах
- •Типы неопределенностей и методы их раскрытия
- •Неопределенность вида .
- •Неопределенность вида .
- •Замечательные пределы
- •Сравнение бесконечно малых функций
- •Практическое занятие №11
- •Григорьев в.П., Дубинский ю.А. «Элементы высшей математики», 2008г.
- •Точки разрыва и их классификация
- •Классификация точек разрыва
- •Практическое занятие №12
- •Производная сложной функции
- •Табличные значения производных основных функций
- •Практическое занятие №13
- •Григорьев в.П., Дубинский ю.А. «Элементы высшей математики», 2008г.
- •Дадаян а.А. «Математика», 2004г.
- •Приближенные вычисления с помощью дифференциала
- •Практическое занятие №14
- •Григорьев в.П., Дубинский ю.А. «Элементы высшей математики», 2008г.
- •Производные высших порядков
- •Раскрытие неопределенностей. Правило Лопиталя
- •Практическое занятие №15
- •Практическое занятие №16
Основные теоремы о пределах
Теорема 1.
![]() ,
где С = const.
,
где С = const.
Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при ха.
Теорема 2.
![]()
Теорема 3.
![]()
Следствие.
![]()
Теорема 4.
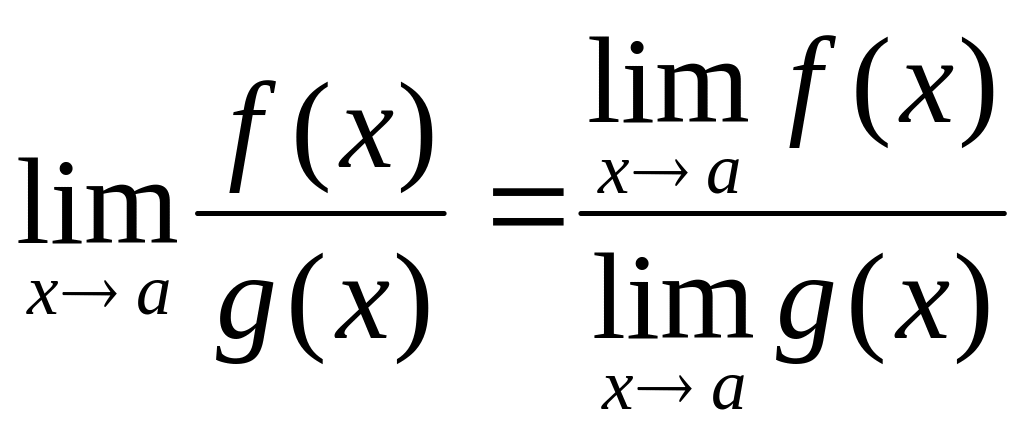 при
при
![]()
Пример. Вычислить предел
![]() .
.
Сначала
найдем предел знаменателя:
![]() =
6∙12 = 6. Предел знаменателя отличен
от нуля, следовательно, можно
воспользоваться теоремами 4, 1:
=
6∙12 = 6. Предел знаменателя отличен
от нуля, следовательно, можно
воспользоваться теоремами 4, 1:
=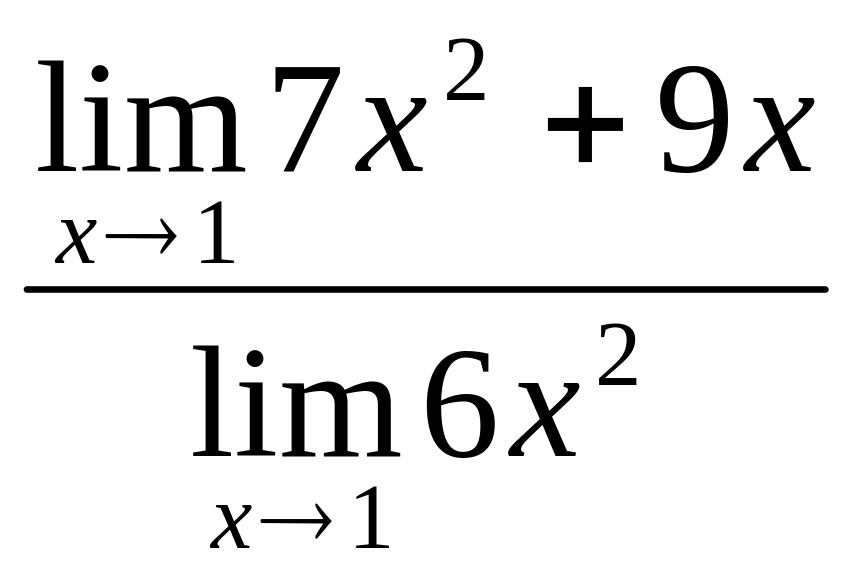 =
=
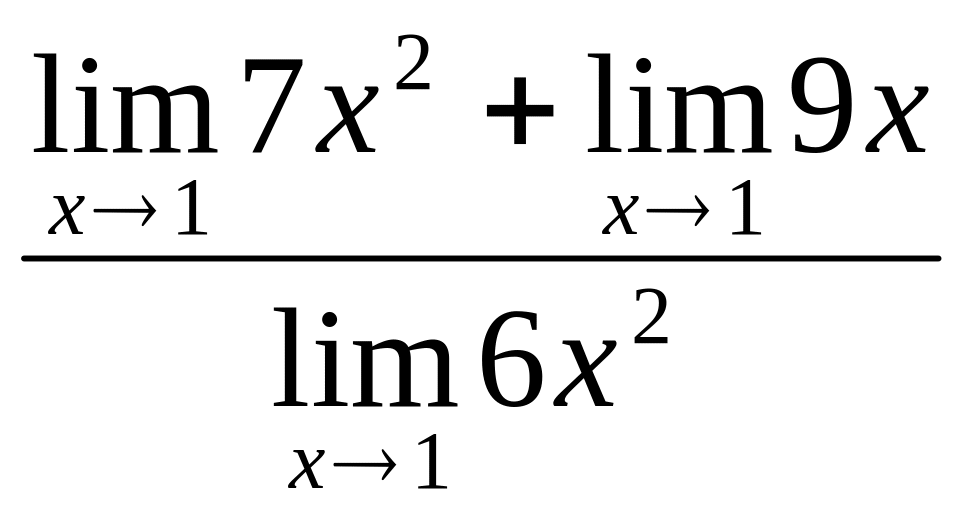 =
=
![]() =
=
![]() =
=
![]()
Функция f(x)
называется бесконечно малой при
ха,
где а может быть числом или одной
из величин ,
+ или
-,
если
![]() .
.
Типы неопределенностей и методы их раскрытия
Часто при вычислении пределов какой-либо функции, непосредственное применение теорем о пределах не приводит к желаемой цели. Так, например, нельзя применять теорему о пределе дроби, если ее знаменатель стремится к нулю. Поэтому часто прежде, чем применять эти теоремы, необходимо тождественно преобразовать функцию, предел которой мы ищем. Рассмотрим некоторые приемы раскрытия неопределенностей.
Неопределенность вида .
Пример. Вычислить предел
![]()
При подстановке вместо переменной х числа -2 видим, что получается неопределенность вида . Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель х+2. В результате получим новый предел, знаменатель которого при подстановке вместо переменной х числа -2 не равен нулю. Этот предел легко вычисляется по теоремам. Таким образом, неопределенность будет раскрыта.
![]()
Пример. Вычислить предел
![]()
При подстановке х =0 получается неопределенность вида .
Умножим числитель и знаменатель дроби на сопряженное числителю выражение:
![]() =
=
![]() .
.
Неопределенность вида .
Для раскрытия этой неопределенности нужно каждое слагаемое числителя и знаменателя разделить на переменную в наибольшей степени и учитывая, что величина обратная бесконечно большой величине есть бесконечно малая величина, раскроем исходную неопределенность.
Пример. Вычислить предел
![]()
Здесь числитель и знаменатель не имеют предела, т.к. оба неограниченно возрастают. В этом случае имеем неопределенность вида . Для ее раскрытия разделим каждое слагаемое на переменную в наибольшей степени, т.е. на х4. Получим:
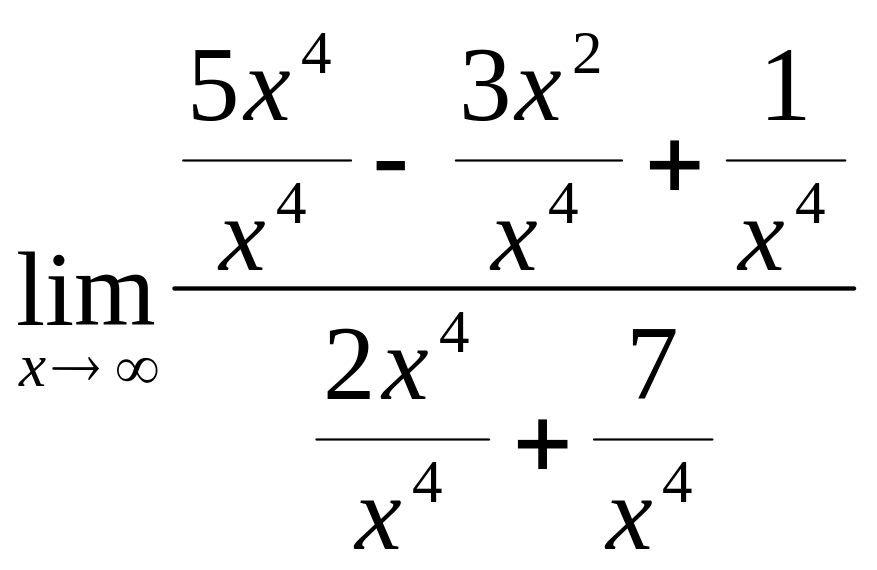 =
=
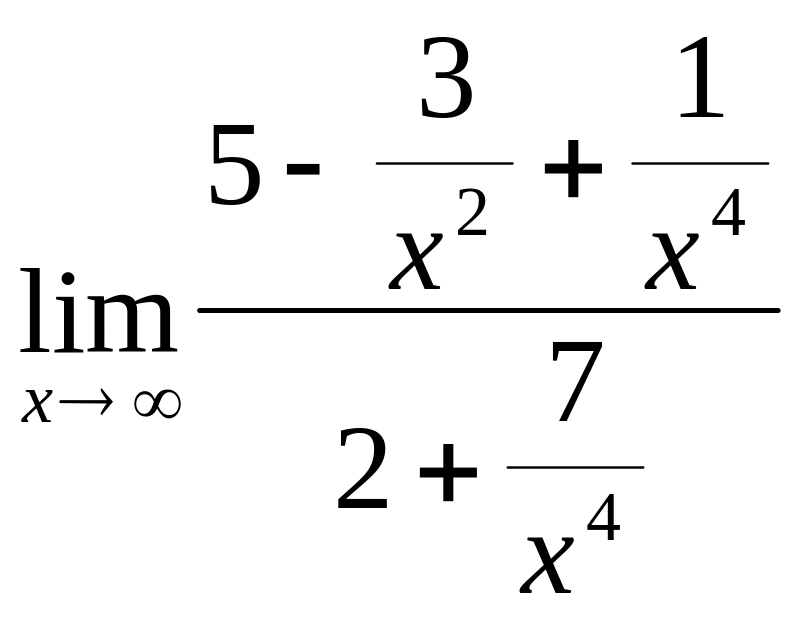 =
=
![]()
Величины
![]() являются бесконечно малыми при
являются бесконечно малыми при
![]() и
их пределы равны нулю. Следовательно,
искомый предел равен
.
и
их пределы равны нулю. Следовательно,
искомый предел равен
.
Пример. Вычислить предел
![]()
Имеем неопределенность вида . Разделим числитель и знаменатель на х2. Получим:
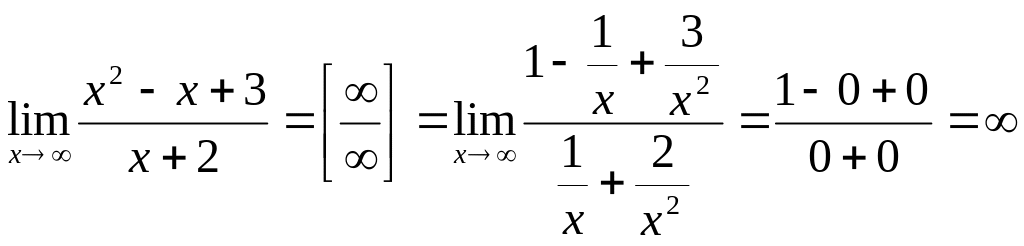
Замечательные пределы
Первый замечательный предел:
![]()
Следствия: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
Второй замечательный предел:
![]()
Следствие:
![]()
Третий замечательный предел:
![]()
Четвертый замечательный предел:
![]() при
при
![]() ,
,
![]() .
.
Часто если непосредственное нахождение предела какой – либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.
Пример. Вычислить предел