
- •Практическое занятие №1
- •Вычислить определитель .
- •Вычислить определитель .
- •Действия с матрицами
- •Определители
- •Способы вычисления определителей:
- •Практическое занятие №2
- •Обратная матрица
- •Ранг матрицы
- •Практическое занятие №3
- •Матричный метод решения систем линейных уравнений
- •Метод Крамера для решения систем линейных уравнений
- •Практическое занятие №4
- •Рассмотрим произвольную систему линейных уравнений. Система m уравнений с n неизвестными в общем виде записывается следующим образом:
- •Метод Гаусса
- •Практическое занятие №5
- •Григорьев в.П., Дубинский ю.А. «Элементы высшей математики», 2008г.
- •Дадаян а.А. «Математика», 2004г.
- •Действия над векторами
- •Координаты вектора
- •Действия над векторами, заданными своими координатами
- •Скалярное произведение векторов в координатной форме
- •Практическое занятие №6
- •Григорьев в.П., Дубинский ю.А. «Элементы высшей математики», 2008г.
- •Дадаян а.А. «Математика», 2004г.
- •Уравнение прямой по точке и нормальному вектору
- •Уравнение прямой по точке и направляющему вектору
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой по точке и угловому коэффициенту
- •Уравнение прямой в отрезках
- •Практическое занятие №7
- •Григорьев в.П., Дубинский ю.А. «Элементы высшей математики», 2008г.
- •Дадаян а.А. «Математика», 2004г.
- •Практическое занятие №8
- •Григорьев в.П., Дубинский ю.А. «Элементы высшей математики», 2008г.
- •Действия с комплексными числами в алгебраической форме
- •Геометрическая форма комплексного числа
- •Практическое занятие №9
- •Григорьев в.П., Дубинский ю.А. «Элементы высшей математики», 2008г.
- •Действия с комплексными числами в тригонометрической и показательной формах
- •Практическое занятие №10
- •Основные теоремы о пределах
- •Типы неопределенностей и методы их раскрытия
- •Неопределенность вида .
- •Неопределенность вида .
- •Замечательные пределы
- •Сравнение бесконечно малых функций
- •Практическое занятие №11
- •Григорьев в.П., Дубинский ю.А. «Элементы высшей математики», 2008г.
- •Точки разрыва и их классификация
- •Классификация точек разрыва
- •Практическое занятие №12
- •Производная сложной функции
- •Табличные значения производных основных функций
- •Практическое занятие №13
- •Григорьев в.П., Дубинский ю.А. «Элементы высшей математики», 2008г.
- •Дадаян а.А. «Математика», 2004г.
- •Приближенные вычисления с помощью дифференциала
- •Практическое занятие №14
- •Григорьев в.П., Дубинский ю.А. «Элементы высшей математики», 2008г.
- •Производные высших порядков
- •Раскрытие неопределенностей. Правило Лопиталя
- •Практическое занятие №15
- •Практическое занятие №16
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
Государственное образовательное учреждение высшего
профессионального образования
«Поволжский государственный университет телекоммуникаций и информатики»
КОЛЛЕДЖ СВЯЗИ
УТВЕРЖДАЮ:
Зам. директора по УПР
_______Черненкова Н.В.
«____»__________2011г.
СБОРНИК
практических занятий
По дисциплине: «Элементы высшей математики»
Номера работ: №1 – 16
для специальностей: 230115 – «Программирование в компьютерных системах»
230401 – «Информационные системы»
Каждая работа рассчитана на 2 часа
Составлен преподавателем Лобачевой М.Е.
Рассмотрен на заседании П(Ц)К
«Естественнонаучные и общепрофессиональные дисциплины»
Протокол № 1 от 31.08.2011г.
Председатель П(Ц)К________Лобачева М.Е.
Самара, 2011г
Практическое занятие №1
Наименование занятия: Операции над матрицами. Вычисление определителей
Цель занятия: Научиться выполнять действия с матрицами, вычислять определители.
Подготовка к занятию: Повторить теоретический материал по теме «Матрицы и определители».
Литература:
Григорьев В.П., Дубинский Ю.А. «Элементы высшей математики», 2008г.
Дадаян А.А. «Математика», 2004г.
Задание на занятие:
Даны матрицы
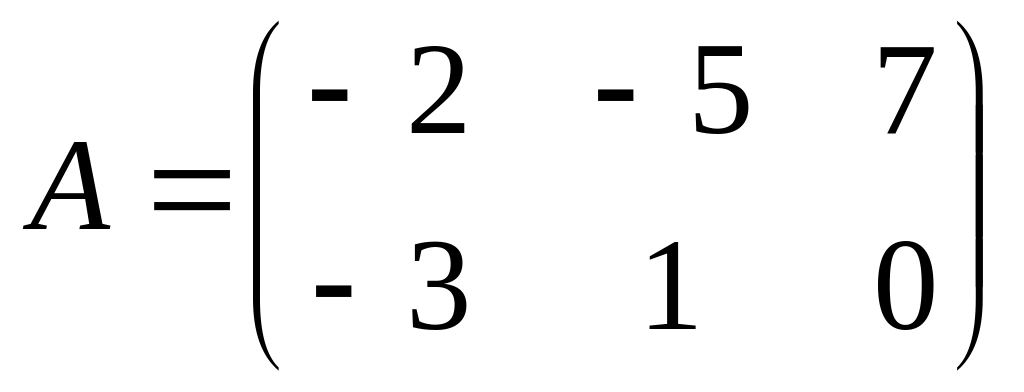 и
и
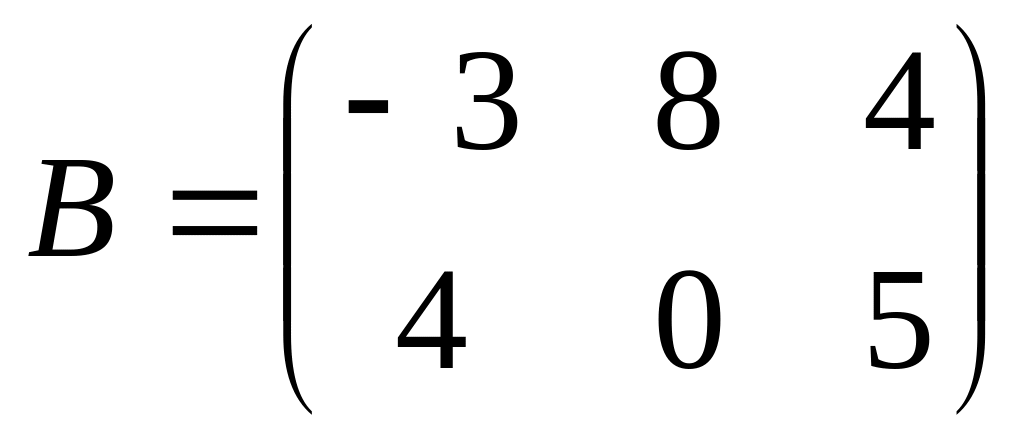 .
Найти матрицу С = 5А – 2В.
.
Найти матрицу С = 5А – 2В.Даны матрицы
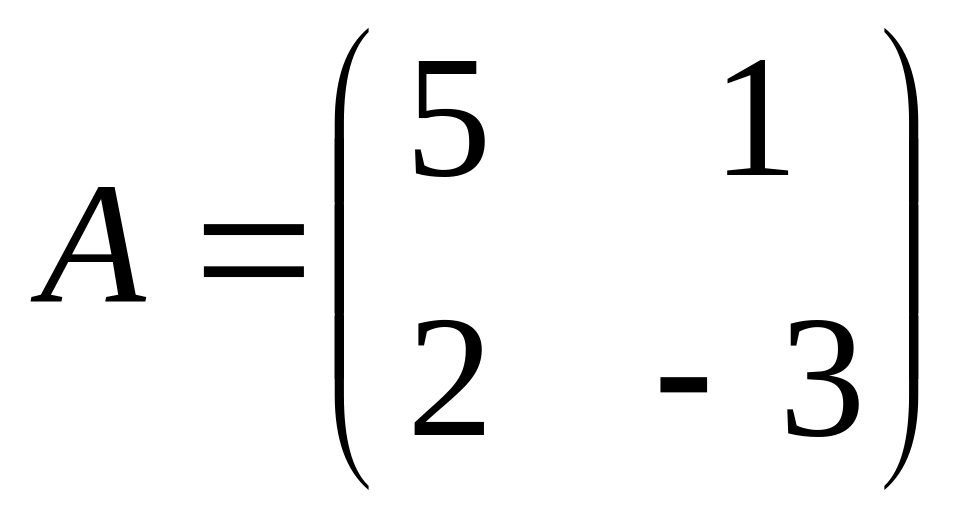 и
и
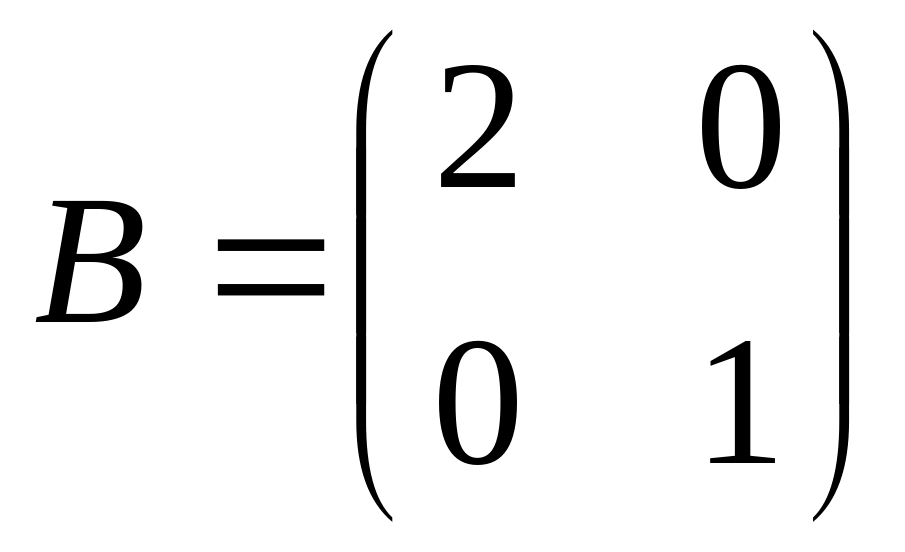 .
Найти матрицу С = АТ·В.
.
Найти матрицу С = АТ·В.Даны матрицы
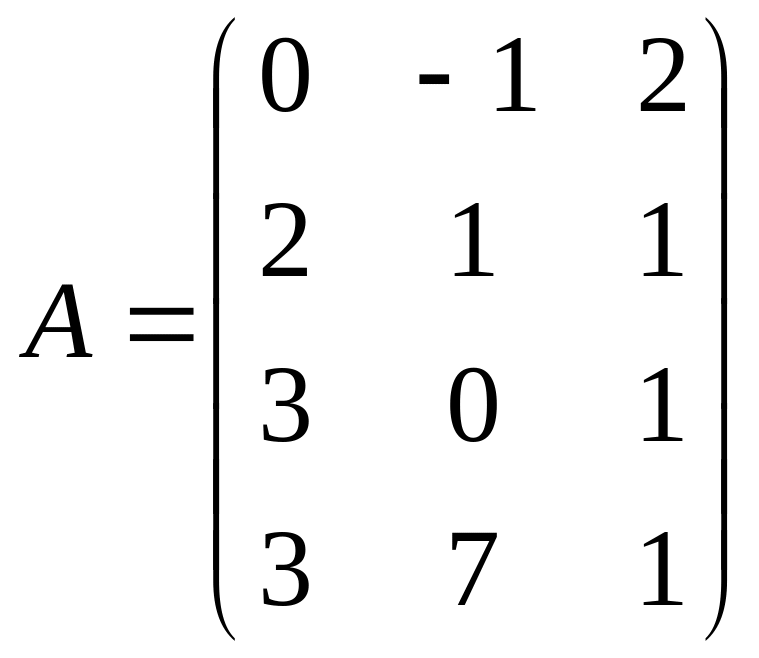 и
и
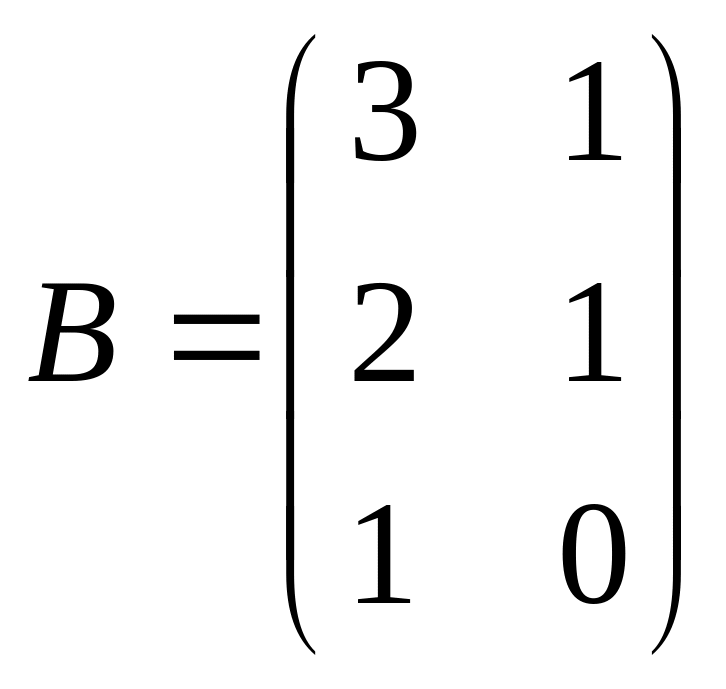 .
Найти матрицу С = А·В.
.
Найти матрицу С = А·В.Даны матрицы
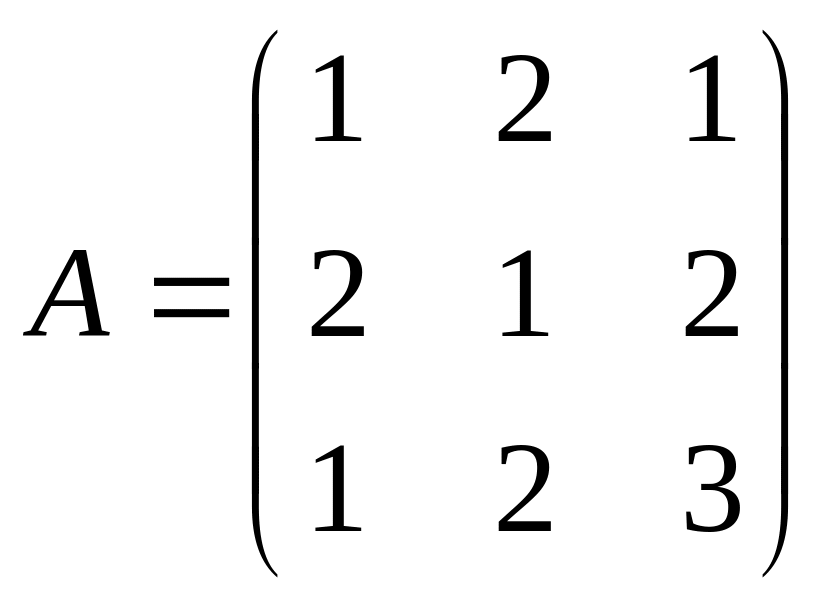 и
и
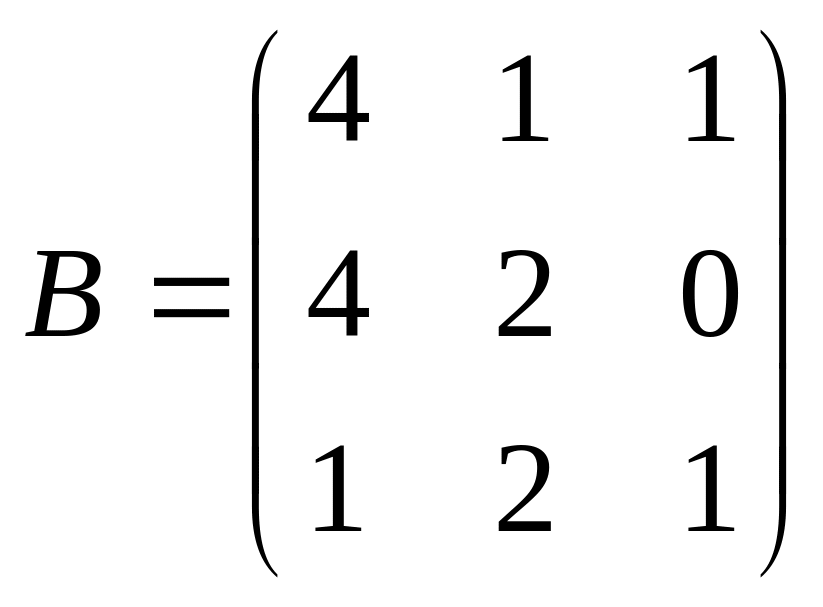 .
Найти матрицу С = А·В – В·А.
.
Найти матрицу С = А·В – В·А.Вычислить определитель
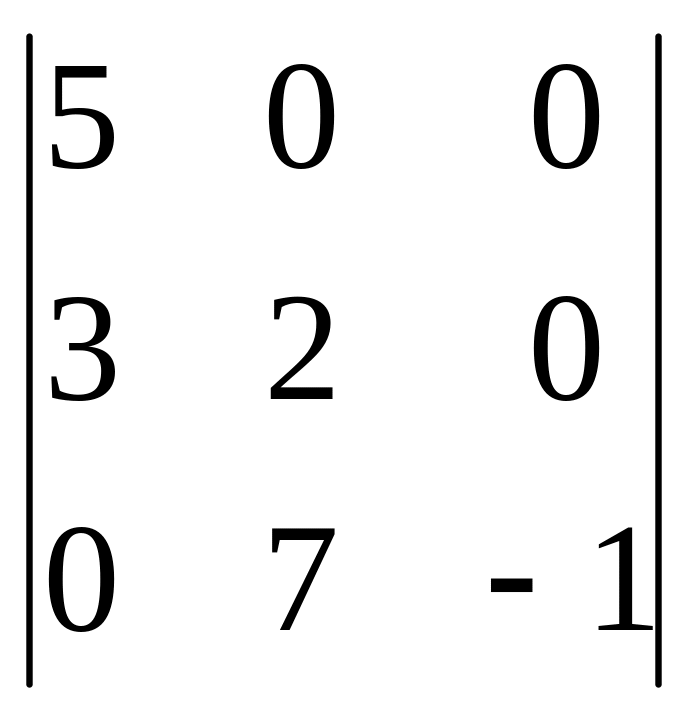 .
.Вычислить определитель .
Вычислить определитель .
Порядок проведения занятия:
Получить допуск к работе
Выполнить задания
Ответить на контрольные вопросы.
Содержание отчета:
Наименование, цель занятия, задание;
Выполненное задание;
Ответы на контрольные вопросы.
Контрольные вопросы для зачета:
Что называется матрицей?
Что называется суммой матриц?
Что называется произведением матрицы на число?
Какая матрица называется транспонированной к матрице А?
Как найти произведение двух матриц?
В чем состоит обязательное условие существования произведения матриц?
Что называется определителем матрицы?
Какие способы вычисления определителей вам известны?
ПРИЛОЖЕНИЕ
Матрицей размера mn, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i- номер строки, а j- номер столбца.
А =
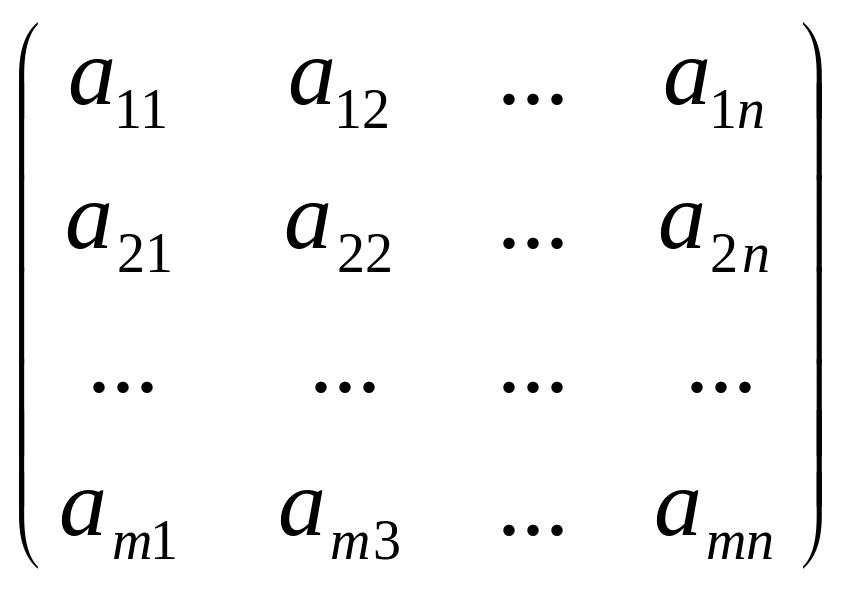
Транспонированной к матрице А
называется матрица
![]() ,
у которой строки и столбцы меняются
местами.
,
у которой строки и столбцы меняются
местами.
Например, А =
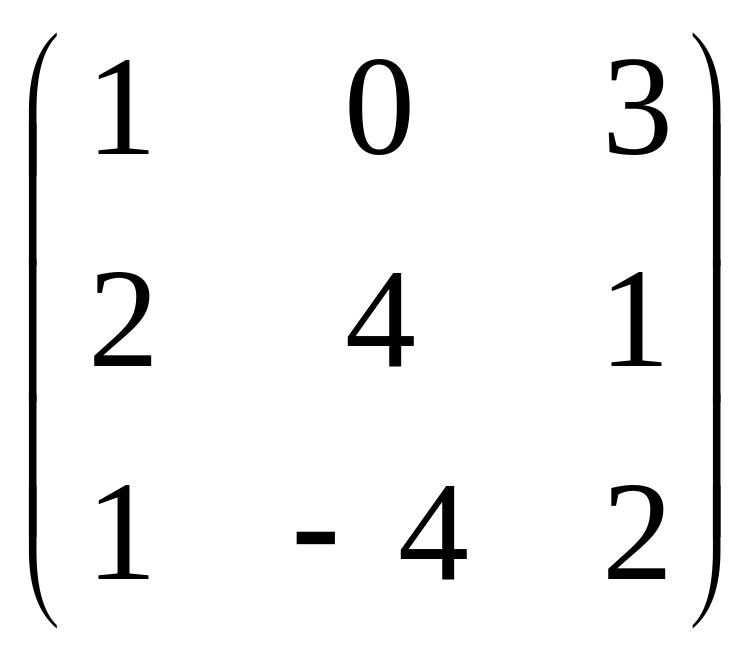 ,
AT =
,
AT =
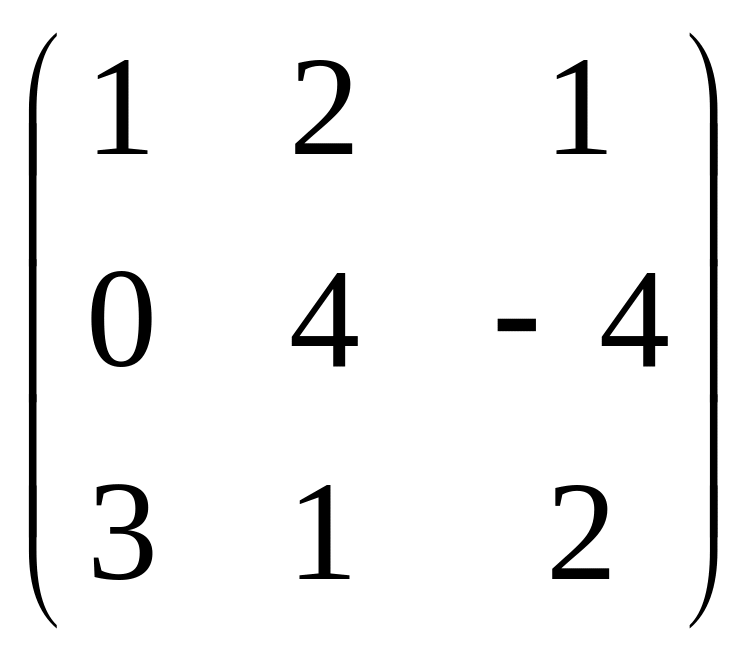 ;
;
Действия с матрицами
Умножение матрицы на число. Для того чтобы умножить матрицу
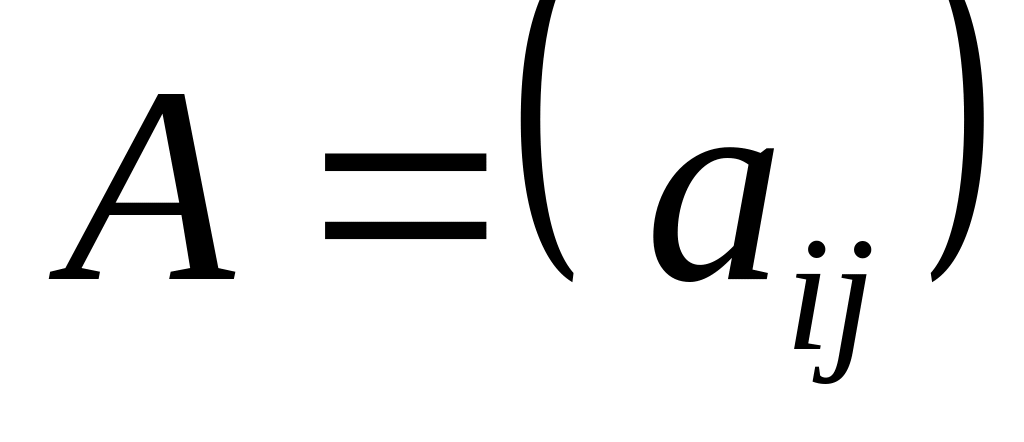 на число
на число
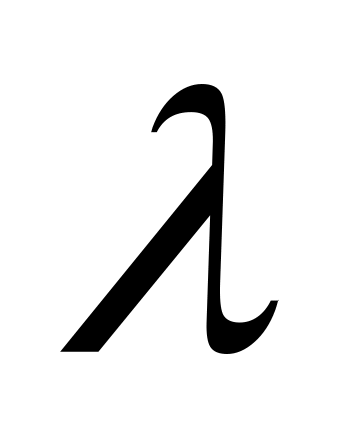 ,
нужно каждый элемент матрицы
,
нужно каждый элемент матрицы
 умножить на это число:
умножить на это число:
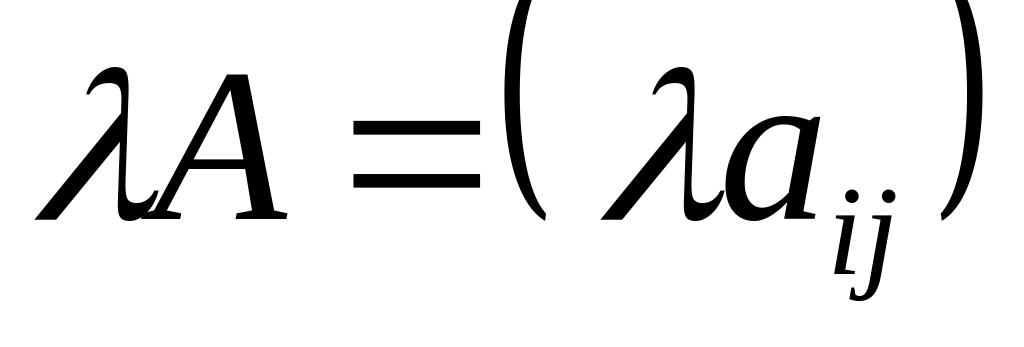 .
.Сложение матриц. Складывать можно только матрицы с одинаковым числом строк и столбцов, т.е. матрицы одинаковых размеров. Суммой матриц и
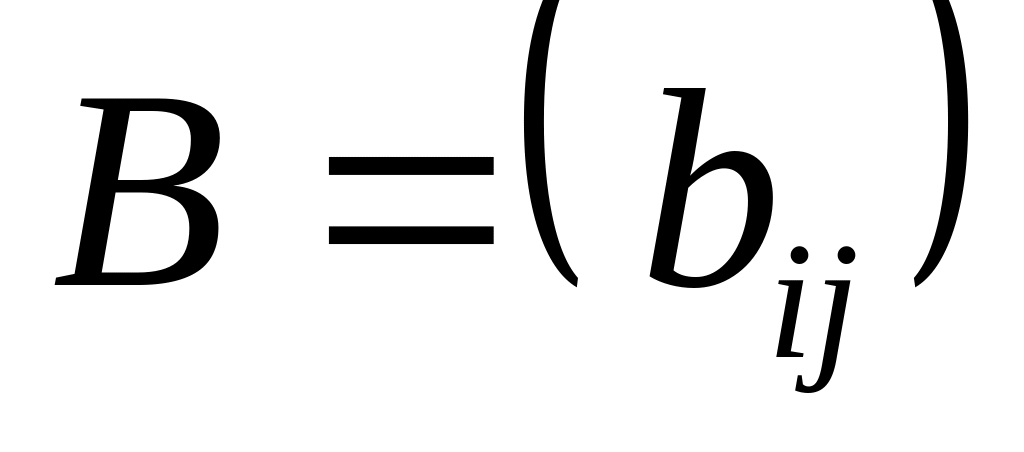 называется матрица
называется матрица
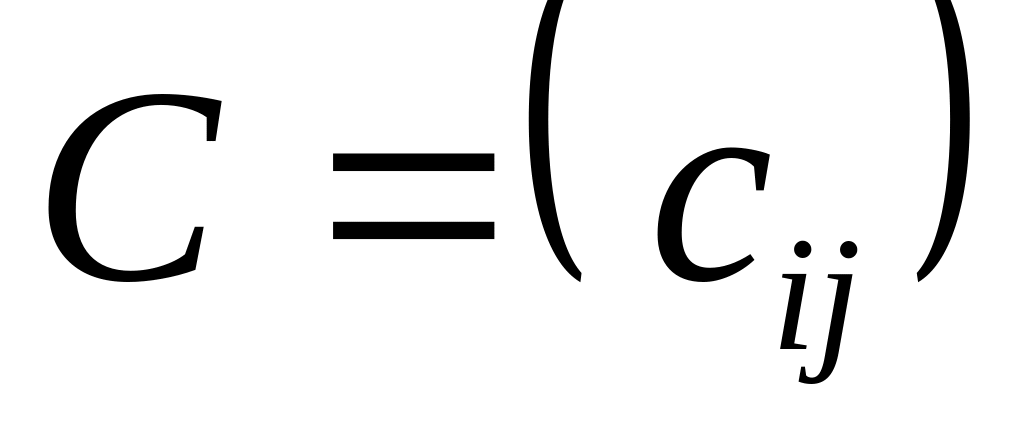 ,
элементы которой равны суммам
соответствующих элементов матриц
,
элементы которой равны суммам
соответствующих элементов матриц
 и
и
 ,
т.е.
,
т.е.
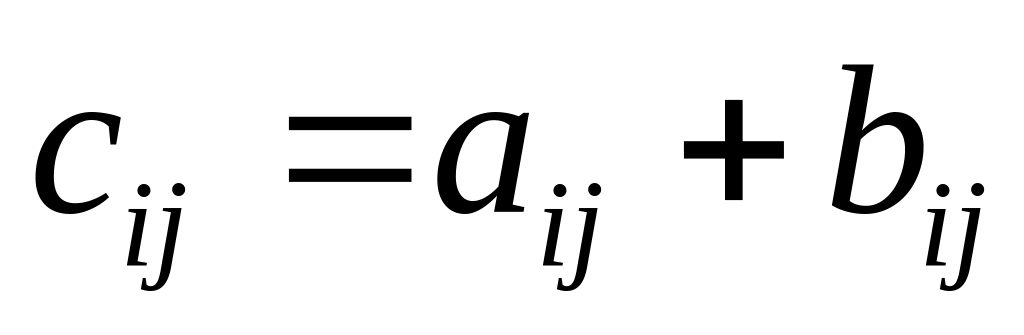 для любых индексов i,
j.
для любых индексов i,
j.
Пример. Даны матрицы А =
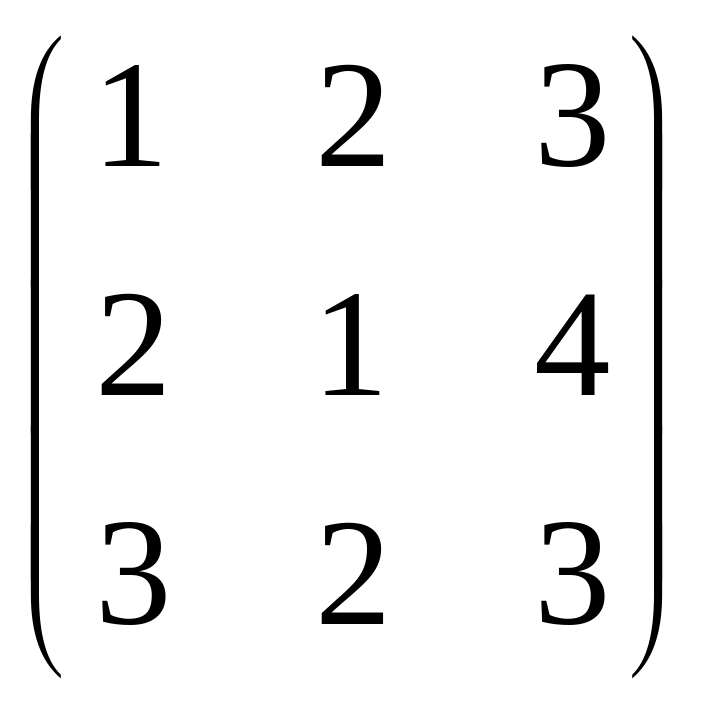 ;
B =
;
B =
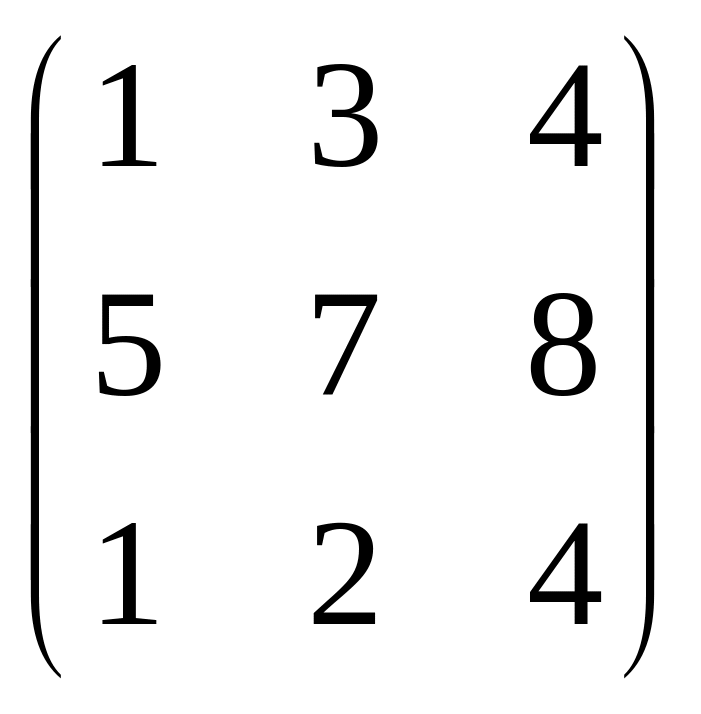 ,
найти 2А + В.
,
найти 2А + В.
2А =
 ,
2А + В =
,
2А + В =
 .
.
3) Умножение матриц. Произведение
матрицы
на матрицу
(обозначается
![]() )
определено только в том случае, когда
число столбцов матрицы
равно числу строк матрицы
.
В результате умножения получим матрицу
)
определено только в том случае, когда
число столбцов матрицы
равно числу строк матрицы
.
В результате умножения получим матрицу
![]() ,
у которой столько же строк, сколько их
в матрице
,
и столько же столбцов, сколько их в
матрице
.
,
у которой столько же строк, сколько их
в матрице
,
и столько же столбцов, сколько их в
матрице
.
Пример. Найти произведение матриц
А =
![]() и В =
и В =
![]() .
.
АВ =
=
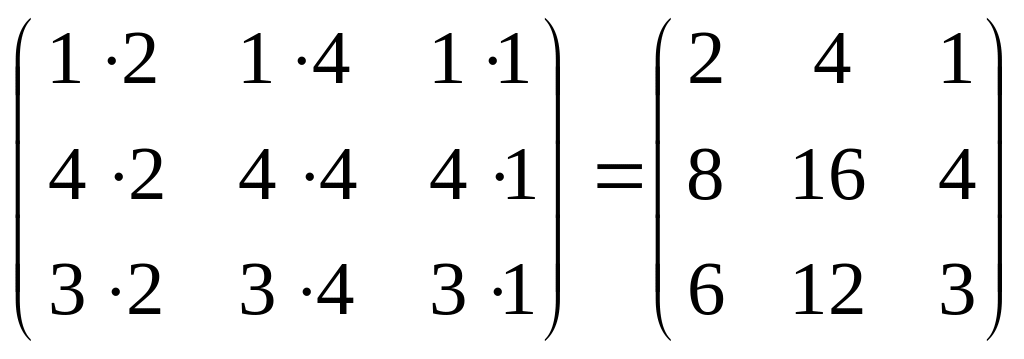 .
.
ВА = = 21 + 44 + 13 = 2 + 16 + 3 = 21.
Пример. Найти произведение матриц
А=![]() ,
В =
,
В =
![]()
АВ =
=
![]() =
=
![]() .
.
Определители
Каждой квадратной матрице
может быть поставлено в соответствие
некоторое число, вычисляемое по
определенному правилу с помощью элементов
матрицы. Такое число называют определителем
(или детерминантом) матрицы
и обозначают символом
![]() или
или
![]() .
При этом порядком определителя
называют порядок соответствующей
матрицы.
.
При этом порядком определителя
называют порядок соответствующей
матрицы.
Правила вычисления определителей 2-го и 3-го порядков легко выписать:
![]() ,
,
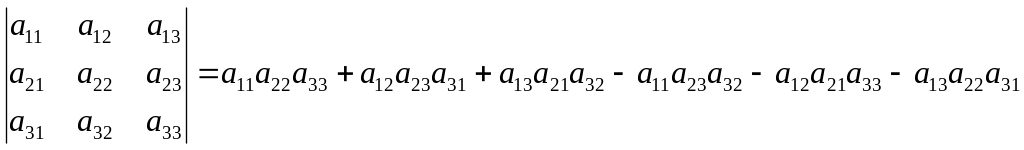
Последнюю
формулу, несмотря на внешнюю сложность
записи, нетрудно запомнить. Если соединить
линией каждые три элемента определителя,
произведение которых входит в правую
часть последней формулы со знаком «![]() »,
то получим легко запоминающуюся схему
1. Аналогично для произведений, входящих
со знаком «–», имеем схему 2.
»,
то получим легко запоминающуюся схему
1. Аналогично для произведений, входящих
со знаком «–», имеем схему 2.
 Схема 1
Схема 2
Схема 1
Схема 2
