§ 6. Наибольшее и наименьшее значение функции

Рассмотрим функцию z = f (x, y), заданную в некоторой замкнутой области , то есть в области, которая включает в себя не только внутренние, но и граничные точки.

Согласно теореме Вейерштрасса, всякая функция, непрерывная в ограниченной и замкнутой области , достигает в этой области своего наименьшего и наибольшего значений. При этом в области найдется по крайней мере одна точка , в которой функция имеет наибольшее (наименьшее) из всех значений. Если эта точка лежит внутри области , то в ней функция имеет абсолютный^) максимум (минимум). Однако функция может достигать своего наибольшего (наименьшего) значения также и на границе области.

Поэтому для нахождения наибольшего (наименьшего) значения функции в области необходимо найти значения функции во всех критических точках области, внутренних и граничных . Наибольшее (наименьшее) из этих значений и является наибольшим (наименьшим) значением функции во всей области . То есть логика поиска наибольшего (наименьшего) значения функции и его алгоритм такие же, как и для функции одной переменной.

П р и м е р 4. Найти наибольшее и наименьшее значения функции в области , ограниченной линиями:

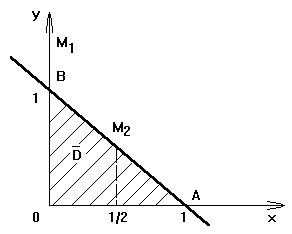
► Сделаем чертеж (рис. 12). Линии, ограничивающие область , являются сторонами треугольника ОАВ. – сторона ОВ; ОА, сторона АВ. Выясним, существуют ли критические точки, лежащие внутри данной области , то есть внутри треугольника ОАВ. Для этого решим систему уравнений

Решая полученную систему, находим критическую точку . Она лежит вне области , следовательно, при решении задачи ее можно не рассматривать. Исследуем функцию на границе области . На стороне ОА треугольника ОАВ (здесь , ) исследуемая функция вырождается в функцию одной переменной . Поэтому в поисках наибольшего и наименьшего значений функции нужно следовать соответствующему алгоритму для функции одной переменной. Критических точек на отрезке ОА нет, так как . На концах отрезка, в точках и А ( 1, 0 ) имеем соответственно z ( 1, 0 ) = 3. На стороне ОВ треугольника ОАВ ( ) также имеем функцию одной переменной ее первая производная равняется Находим критическую точку, рассматривая , то есть . Получаем . Это точка , она также не принадлежит области . Остается найти значение функции на конце отрезка ОВ, в точке Находим наибольшее и наименьшее значения функции на стороне АВ. Здесь , поэтому , то есть исследуемая функция двух переменных на границе АВ также вырождается в функцию одной переменной. Исследуем эту функцию на наибольшее (наименьшее), на отрезке , из следует . Таким образом, на границе АВ области имеем критическую точку Значение функции в этой точке . Сравнивая все полученные значения функции, видим, что а ◄

§ 7. Метод наименьших квадратов. Аналитическое описание экспериментальных данных

Изучение взаимосвязи экономических показателей является одной из основных задач экономического анализа. В частности, для того, чтобы средствами налоговой и кредитно-денежной политики воздействовать на темп инфляции, нужно знать и постоянно отслеживать зависимость между предложением валюты и уровнем цен на нее. Если наблюдаемая зависимость описана аналитически, появляется возможность анализа ситуации и прогноза ее дальнейшего развития. Таким образом, возникает необходимость аналитического описания экспериментально наблюдаемых зависимостей.

Предположим, что зависимость между двумя переменными, назовем их и , полученная опытным путем, представлена в виде таблицы. Это могут быть результаты статистической обработки материала, эксперимента или наблюдения. Требуется с помощью соответствующей эмпирической^) формулы описать наблюдаемую функциональную зависимость от , исключив при этом случайные отклонения, связанные с неизбежными погрешностями измерений или статистических наблюдений.

Одним из наилучших методов получения эмпирических формул является метод наименьших квадратов. В его основе лежит поиск экстремального значения функции нескольких переменных. Рассмотрим этот метод на простейшем примере.

Пусть в результате наблюдений установлено, что соответствует и т.д., то есть , имеем таблицу:

x1	x2	x3	…	xi	…	xn
y1	y2	y3	…	yi	…	yn

Если ( ; ) рассматривать как координаты точки на плоскости, то результаты наблюдений можно рассматривать, как множество точек, группирующихся вдоль некоторой линии на плоскости. Будем считать, что изучаемая функциональная взаимосвязь является в первом приближении линейной, и полученные данные достаточно хорошо укладываются на прямую . Заметим, что при подстановке в уравнение прямой, по формуле должно получиться , а эксперимент дает . То есть формула дает расхождение с экспериментом. Назовем это несоответствие отклонением . Оно равно . Расхождение с экспериментом связано с ошибками эксперимента и вычислений, а неабсолютной линейностью изучаемой зависимости и т.п., с неудачно выбранными параметрами прямой и . Естественно считать, что прямая, наилучшим образом описывает результаты наблюдений, если отклонения координат точек прямой от экспериментально наблюдаемых минимальны. Поэтому неизвестные параметры уравнения и прямой следует подобрать таким образом, чтобы сумма квадратов отклонений была минимально возможной. Можно брать и другие четные (подумать почему) степени . Но нельзя рассматривать сумму самих отклонений. Она может получиться малой при больших по абсолютной величине слагаемых разного знака.

Итак, сумма должна быть минимальной. Поскольку эта сумма представляет собой функцию двух переменных и ( и – известные нам величины. Это результаты наблюдений, сосредоточенные в таблице), то задача сводится к исследованию этой функции на экстремум. Нужно выяснить при каких значениях и функция имеет минимум.

Введем обозначение . Если – экстремальная точка функции , то скорость изменения функции в этой точке равна нулю, (подумать почему) следовательно, равны нулю все составляющие скорости, то есть и . Найдем частные производные и рассмотрим соответствующую систему уравнений.

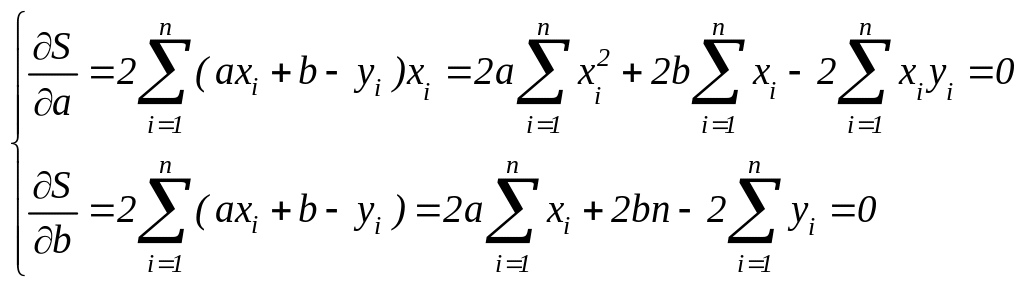
или 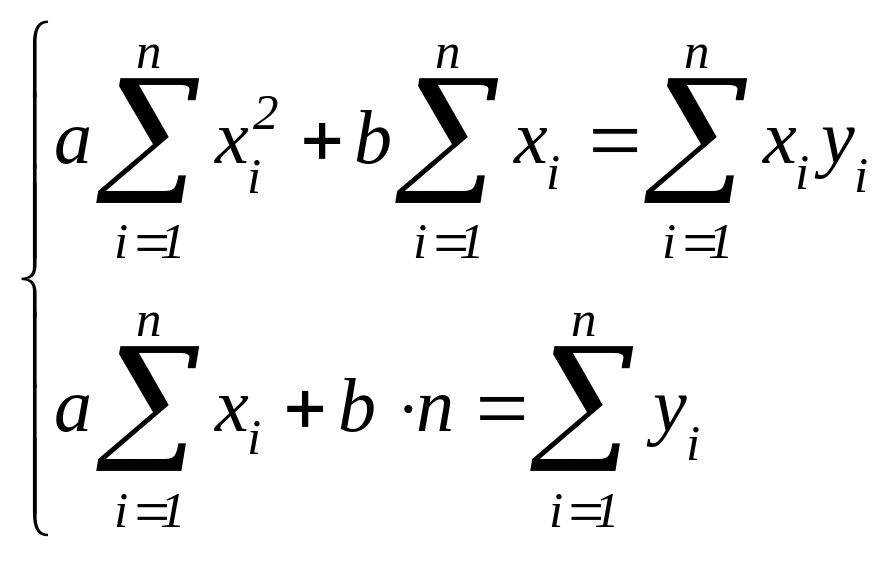(1)

Систему (1) принято называть нормальной системой метода наименьших квадратов. Чтобы найти решение этой системы, нужно предварительно вычислить суммы и , являющиеся коэффициентами при неизвестных и .

Рассмотрим пример поиска эмпирической формулы.

Допустим, что в результате эксперимента обнаружено, что переменные и взаимосвязаны. Их взаимосвязь отражена в следующей таблице:

x	1	2	3	4	5
y	3.8	4.8	3.3	1.3	1.8

Нужно выяснить характер наблюдаемой взаимосвязи и описать ее аналитически.

Чтобы получить наглядное представление о наблюдаемой функциональной зависимости, воспользуемся графической интерпретацией имеющихся данных.

П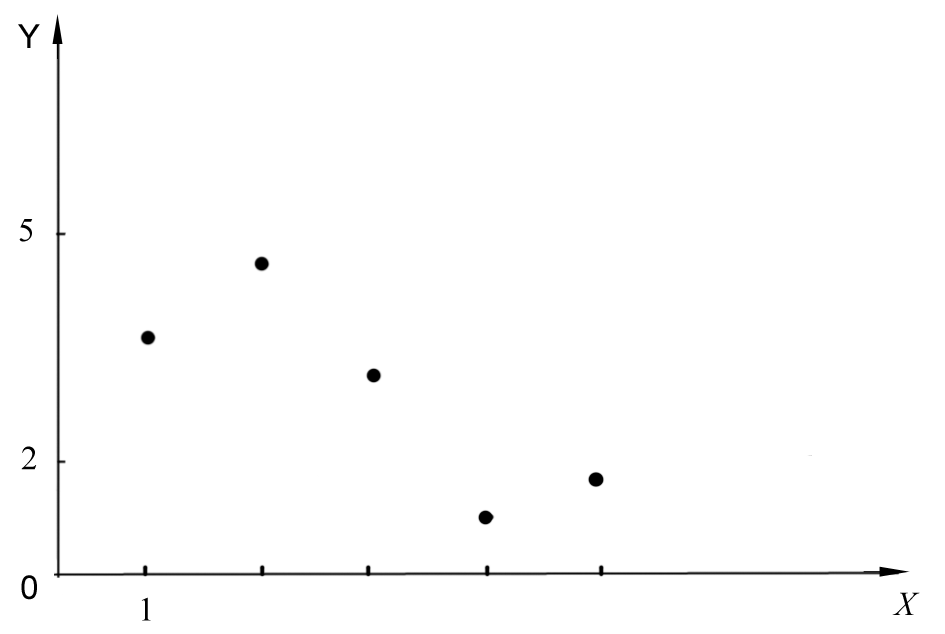 олученный рисунок (рис. 13) показывает, что наблюдаемую зависимость можно считать в первом приближении линейной, то есть описываемой уравнением . Чтобы отклонения экспериментальных данных от прямой, которая их описывает были наименьшими из всех возможных, найдем параметры прямой и по методу наименьших квадратов. Составим нормальную систему (1) метода наименьших квадратов. Для этого найдем коэффициенты и свободные члены этой системы, то есть суммы и . Будем иметь

_{Подставив эти данные в (1), получим}

Решая систему, имеем . Значит, функция является наилучшей линейной зависимостью при описании имеющихся экспериментальных данных. И отклонения экспериментальных данных от прямой являются наименьшими из возможных при линейной интерпретации наблюдаемой функциональной взаимосвязи переменных и .

⁾ Абсолютный максимум (минимум) – наибольшее (наименьшее) значение функции среди всех локальных максимумов (минимумов) в области .

⁾Формулы, полученные при аналитическом описании опытных данных, носят название эмпирических формул.