15.3 Аналитические исследования

15.3.2 Методы механики сплошной среды

Подавляющее число моделей механики горных пород в той или иной степени основано на теории упругости. В связи с этим важно рассмотреть основные уравнения теории упругости, описывающие деформирование участка массива горных пород. Напряжения, действующие в горном массиве можно представить в виде нормальных и касательных компонент, действующих на площадках, перпендикулярным к осям X, Y, Z в декартовой системе координат (рисунок 15.20).

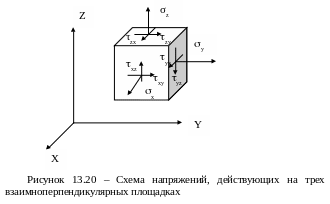
Нормальные _x, _у, _z и касательные _xy, _yz, _xz напряжения неразрывно связаны с соответствующими деформациями _x, _у, _z, и _xy, _yz, _xz взаимно порождая друг друга. Деформации определяются дифференцированием смещений точек горного массива u, v, w вдоль осей X, Y, Z. Относительные удлинения или укорочения вдоль соответствующих осей определяются по зависимостям:

_x=du/dx, _у=dv/dy, _z=dw/dz (15.9)

Относительные сдвиги описываются такими формулами:

_xy=du/dy + dv/dx, _yz=dv/dz + dw/dy, _xz=du/dz + dw/dx (15.10)

Выделение нормальных и касательных компонент деформаций, вообще говоря, условно и сделано для удобства математической интерпретации процесса деформирования твердого тела. Так нормальные компоненты деформации описывают отдельно изменение объема тела, а касательные характеризуют только изменение формы тела в процессе его деформирования. Согласно правилам теории упругости массив горных пород должен деформироваться без разрывов сплошности, причем деформации в нем распределены непрерывно, без скачкообразных изменений. Это так называемое условие сплошности деформаций описывается следующими уравнениями.

(13.11)

При условии статического равновесия среды деформирование участка массива горных пород должно подчиняться условию равновесия, описываемого такими формулами.

(15.12)

где F_x, F_y, F_z – компоненты объемных сил, действующих в массиве горных пород.

Если рассматривается динамическая задача, в правой части уравнений (15.4) вместо нулей появляются силы инерции.

Напряжения и деформации связаны зависимостью, в которой используются такие деформационные свойства горных пород, как модуль упругости Е и коэффициент Пуассона μ. Для изотропной среды, свойства которой во всех направлениях одинаковы, применяются только один модуль упругости и один коэффициент Пуассона. Примером такой среды может служить участок горного массива, сложенного песчаником, бетонная крепь капитальной горной выработки и др. При анизотропной среде следует учитывать деформационные константы среды в двух и даже в трех направлениях, что усложняет формулы, связывающие напряжения и деформации. Для изотропной среды связь между напряжениями и деформациями описываются формулами

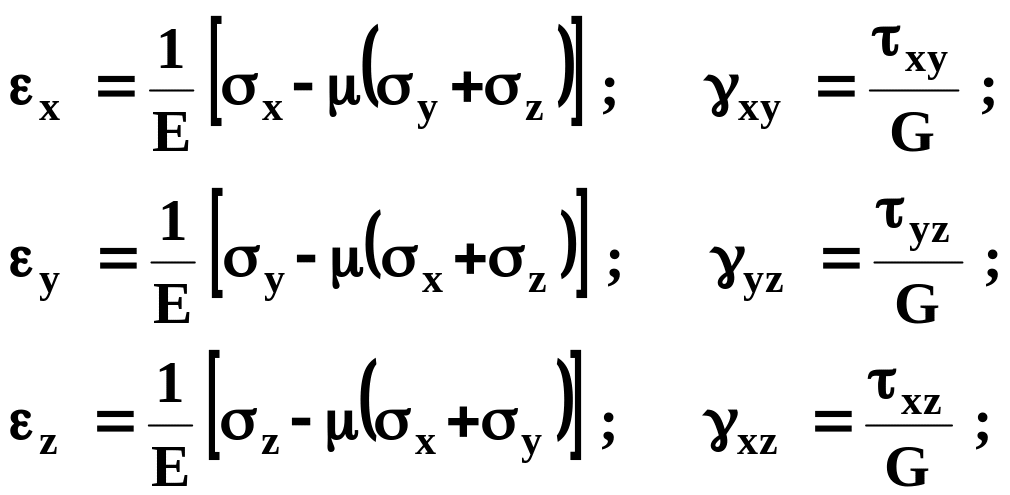(15.13)

где G является модулем сдвига.

Относительное изменение объема и упругую потенциальную энергию объема изотропного горного массива определяют по формулам

= _x_y_z

(15.14)

Последняя формула часто применяется при оценке прочности горного массива, в частности она используется в энергетической теории внезапных выбросов.

Отметим также, что в теории упругости возможно использование метода суперпозиции сил, когда результирующая сила в одной точке тела может быть найдена путем суперпозиции или наложения действия любого количества других сил, приложенных за пределами рассматриваемой точки. Этот метод будет часто использоваться в дальнейшем.

Покажем на простейшем случае, как находятся компоненты напряжений и деформаций вокруг подготовительной выработки аналитическим путем. Подчеркнем, что аналитическое решение задачи можно получить лишь в ограниченном числе случаев, которые характеризуются простейшими условиями. В данном примере массив будет представлен простейшей геомеханической однородной изотропной линейно деформируемой моделью. Это значит, что модуль упругости и коэффициент Пуассона в таком массиве имеют постоянное значение во всех направлениях, причем массив состоит из одной породы, то есть неслоистый и не содержит включений и деформируется без разрушений и пластических или вообще необратимых деформаций. Начальное напряженное состояние примем равнокомпонентным, когда все три главные нормальные напряжения равны между собой.

; (15.15)

При этом ось z направлена вдоль оси выработки, r совпадает с направлением радиуса, проведенного под углом θ к вертикали (рисунок 15.21). Давление на глубине заложения выработки соответствует величине q. Горизонтальная выработка имеет круговое сечение.

Для указанных условий можно воспользоваться упрощенным решением осесимметричной задачи, когда распределение деформаций и напряжений зависит только от расстояния до центра выработки и не зависит от угла, в направлении которого рассматривается распределение. Если выработка имеет значительную протяженность и все ее вертикальные сечения равноценны, можно рассматривать их в состоянии плоской деформации с осевой симметрией.

Расчетная схема приведена на рисунке 15.21, а граничные условия имеют вид

(15.16)

где р означает отпор крепи. Стремление напряжений к нулю на бесконечности говорит о том, что пока мы рассматриваем только дополнительные напряжения, возникающие в массиве от возмущения исходного поля напряжений после проведения выработки. Полные напряжения будут определены позже.

Д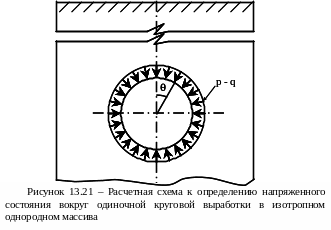 ля таких упрощенных условий система уравнений, описывающая напряженно-деформированное состояние массива более простой вид. При этом уравнение равновесия упрощается к виду

(15.17)

Упрощая еще задачу, примем, что коэффициент Пуассона равен 0,5. Такое состояние близко к тому, которое имеет место в водонасыщенных глинистых породах. В этом случае уравнение неразрывности деформаций имеет вид:

(15.18)

И физическое уравнение связи деформаций с напряжениями тоже упрощается к такой формуле

(15.19)

Решение уравнения неразрывности деформаций достигается специальным математическим приемом путем введения так называемой функции напряжений F. Эту функцию связывают с напряжениями следующими формулами

, (15.20)

Тогда уравнение неразрывности деформаций с учетом (15.19) преобразуется к виду

(15.21)

Решением этого уравнения является следующая функция напряжений

(15.22)

При этом в случае однородного изотропного массива она упрощается к виду

(15.23)

Теперь используя формулы (15.20), из граничных условий (15.16) находим выражения для констант интегрирования: С₃=0; С₁=(p-q).

После этого определяем компоненты дополнительных напряжений:

(15.24)

Полные напряжения находим в результате суммирования дополнительных и исходных.

(15.25)

К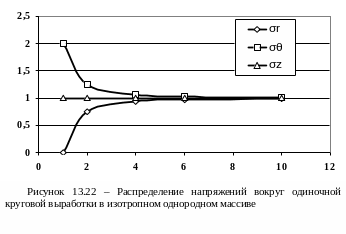 омпоненты деформаций определим из выражения (15.19), подставив в них дополнительные напряжения.

(15.26)

Другими словами с точки зрения податливости крепи и ее целостности, нас интересуют только дополнительные деформации массива после проведения выработки. Наоборот, полные напряжения нам нужны для правильной оценки возможности разрушения массива на контуре выработки. Радиальные безразмерные смещения в этом случае равны

(15.27)

Анализ закономерности распределения напряжений вокруг сечения круговой выработки показывает (рисунок 15.22), что тангенциальное напряжение на контуре имеет максимальную величину, причем коэффициент концентрации равен 2, что подтверждается во многих случаях на практике. Радиальная компонента напряжений на контуре имеет минимальное значение (нулю при незакрепленном контуре и р в обратном случае). По мере удаления от контура выработки вглубь массива напряжения стремятся к величинам, соответствующим исходному уровню напряжений до проведения выработки. Такое положение наблюдается на расстоянии 4-5 радиусов выработки, что также хорошо совпадает с величиной, замеренной в натурных условиях.

Подчеркнем, что, несмотря на большое число допущений, и принятых упрощений, такие важные параметры проявления горного давления вокруг одиночной выработки, как величина концентрации напряжений на ее контуре и радиус зоны существенного влияния выработки на окружающий массив достаточно хорошо согласуются с величинами, установленными в натуре. Это свидетельствует о правомерности применения теории упругости для описания напряженно-деформированного состояния массива вокруг одиночной выработки для простых исходных условий.

Применение методов конечных разностей для расчета напряженного состояния массива горных пород часто встречается в геомеханических расчетах.

И

σ_r

σ_θ

σ_z

дея метода конечных разностей состоит в том, что любое дифференциальное уравнение, в том числе и в частных производных, или система таких уравнений, могут быть заменены системой конечно-разностных алгебраических уравнений. Другими словами, математическая производная (как предел, к которому стремится отношение приращение функции к приращению аргумента при стремлении аргумента к нулю) заменяется приближенной производной, отражающей отношение приращение функции к приращению аргумента на конечном интервале. Таким образом, непосредственное дифференцирование заменяется численным. Это обстоятельство дает возможность учитывать весьма широкий круг граничных условий, недоступных непосредственному дифференцированию. Численное решение задач теории упругости поэтому применяется в условиях, когда нужно решать сложные задачи, реально возникающие в практике горного дела. Покажем это на примере расчета перераспределения горного давления в окрестности очистных работ, реализуемого методом конечных разностей.

Рассмотрим область горного массива, затронутую очистными работами (рисунок 15.23). Перекрывающие выработанное пространство слои пород можно представить как плиту мощностью h, покоящуюся на неоднородном основании. Жесткость этого основания максимальна в нетронутом массиве (К1) и минимальна над выработанным и обрушенным пространством (К2). В местах закладки и сооружения других искусственных сооружений величина жесткости имеет промежуточное значение. Толщина породного слоя, перекрывающего выработанное пространство и определяющего перераспределение горного давления, составляет, как правило, 25-50м. По сравнению с типичной шириной минимального выработанного пространства, образованного отработкой одной лавы толщина определяющего слоя в 5-10 раз меньше.

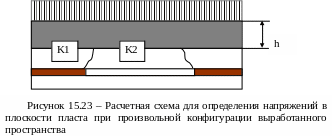
Это дает основание рассматривать указанный слой как тонкую плиту, опирающуюся на неоднородное основание и пригруженную весом вышележащей толщи. Прогибы такой плиты описываются дифференциальным уравнением в смешанных производных четвертого порядка.

(15.28)

где  – прогибы точек плиты;

q – нормальная к срединной плоскости и распределенная по поверхности плиты пригрузка от вышележащей толщи;

K – коэффициент жесткости основания, изменяющийся в зависимости от наличия или отсутствия выработанного пространства;

D -цилиндрическая жесткость плиты; , где h - мощность плиты.

Численная производная берется как отношение приращения функции (в данном случае опускания точек плиты) к приращению аргумента (в данном случае длины участка, на котором определяется производная) в соседних точках расчетной сетки, на которую разбивается анализируемая область. В принципе для приближенного определения производной необходимо значения функции хотя бы в двух соседних точках расчетной сетки. Чем выше порядок производной, тем больше соседних точек необходимо для определения производной. Например, производная первого порядка от функции y при постоянном интервале численного дифференцирования (приращении аргумента) h определяется по формуле

(15.29)

Производная второго порядка находится по зависимости

(15.30)

И т.д. Для численного нахождения производных из уравнения (15.28) приведен на рисунке 15.24 шаблон, согласно которому удобно рассчитывать приближенную производную опусканий плиты.

В результате дифференциальное уравнение (15.28) заменяется конечно-разностным аналогом для прямоугольной сетки с размерами элементарной ячейки а и b

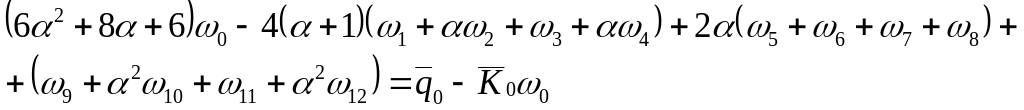(15.31)

где ; – приведенная интенсивность внешней нагрузки в центральной точке О конечно-разностного ромбовидного эквивалента (рисунок 15.24).

– приведенный коэффициент жесткости основания в точке О.

Составление конечно-разностных уравнений производится для всех точек плиты. Эту весьма громоздкую работу берет на себя компьютер, поскольку в точках, примыкающих к границам плиты, ромбовидный шаблон становится усеченным из-за отсутствия ряда соседних узлов, что меняет вид уравнения. На рисунке 15.25 приведена блок-схема программы расчета опусканий в точках плиты на неоднородном основании. Работа программы начинается с ввода исходных данных, к которым относятся геометрические характеристики плиты, расчетной разностной сетки, а также деформационные характеристики плиты и основания. Для экономии времени подготовки исходные данные могут вводиться только на границах расчетной и характерных областей, а в тех местах, где исходные параметры постоянные, входные величины просто размножаются.

Далее следует автоматическое вычисление коэффициентов при неизвестных прогибах в зависимости от местоположения расчетного узла сетки. Наиболее трудоемкой процедурой является решение системы алгебраических уравнений:

(15.32)

где [W] – вектор-строка опусканий узловых точек;

[NL] – матрица коэффициентов при неизвестных;

[q] – вектор-столбец заданных узловых нагрузок.

В результате решения системы (15.32) получаем вектор опусканий узлов плиты. По этим величинам находим все силовые факторы плиты по формулам:

Нормальное контактное давление в основании плиты

(15.33)

погонный изгибающий момент в направлении оси Х

(15.34)

погонный изгибающий момент в направлении оси У

(15.35)

погонный крутящий момент

(15.36)

погонная поперечная сила в направлении оси Х

(15.37)

погонная поперечная сила в направлении оси У

(15.30)

Нетрудно убедиться, что при вычислении производных часто используют формулы типа (15.29) и (15.30). Контактное давление используют для оценки зон ПГД, опорного давления, зон разгрузки. Изгибающие моменты применяют для оценки разрушений плиты-кровли от нормальных напряжений. Как правило, для горных пород предельное состояние определяют прежде всего по растяжению, прямо пропорциональному изгибающему моменту и обратно пропорциональному моменту сопротивления сечения плиты-кровли. По крутящему моменту и поперечным перерезывающим силам определяют предельное состояние плиты кровли по касательным нагрузкам. Имея паспорт прочности породы кровли, можно определить на основании полученных силовых характеристик плиты-кровли ее возможное запредельное состояние в любой расчетной точке.

Вышеописанный алгоритм является весьма эффективным инструментом для оценки напряженного состояния кровли пласта и прилегающего к нему массива горных пород. Преимущество данного метода состоит в том, что он обрабатывает широкий диапазон граничных условий. Для аналитического метода решения дифференциального уравнения (15.28) даже незначительное усложнение граничных условий приводит к катастрофическому усложнению задачи.

Уравнения 15.915.14 достаточны для определения всех неизвестных компонент напряжений, деформаций и перемещений, если известны граничные условия. Полученные решения должны удовлетворять условиям на контуре, например статическим граничным условиям на границах расчетной области и на контуре исследуемой горной выработки. Однако во многих случаях, имеющих практический интерес, геометрическая конфигурация среды, граничные условия и строение реального горного массива настолько сложны, что не позволяют определить напряженно-деформированное состояние в замкнутом виде, то есть в виде алгебраических формул. Поэтому в подавляющем числе случаев прибегают к приближенным или численным методам решения уравнений теории упругости. Часто такие методы основаны на вариационном принципе, согласно которому действительная форма равновесия системы «горная выработка – окружающий массив» отличается от всех мыслимо возможных форм тем, что полная потенциальная энергия системы имеет стационарное (в частности, минимальное) значение. Проиллюстрируем сущность сформулированного положения на примере простой задачи. Стержень сечением s, с модулем упругости Е и длиной l закреплен одним концом и растягивается осевой силой Р. При этом, он удлиняется на неизвестную длину l. Приняв Р = 100 кН, s = 1 см², l = 1 м, и Е = 10 ГПа, по формуле Гука получим растяжение, равное l=Pl/(sE)=0,1 м.

Теперь определим ту же величину, основываясь на вариационном принципе. В результате приложения к стержню силы Р происходит его деформация и меняется потенциальная энергия системы Э, которая может быть выражена как

Э=U-W, (15.39)

где U- потенциальная энергия деформации; W – потенциал внешних сил.

Потенциальная энергия деформации элементарного объема стержня равна 0,5 (см. формулу 15.6). Для всего стержня она равна U=0,5sl. Потенциал внешних сил есть произведение силы на перемещение конца стержня, то есть W=Pl. Произведя подстановки =Е и =l/l, получим

Э=0,5l²sE/l - Pl (15.40)

В соответствии с вариационным принципом действительной форме стержня после его деформации будет соответствовать та, при которой Э примет минимальное значение. Это значит, что первая производная потенциальной энергии системы по перемещению должна быть равна нулю. На графике рисунка 15.26 видно, что минимальное значение потенциальная энергия деформации принимает действительно при величине растяжения стержня, равной 0,1м.

И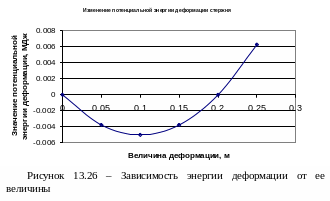 дея, заложенная в вариационном принципе механики, используется во многих численных методах, например в методе конечных элементов.

Метод конечных элементов (МКЭ) применяется при решении широкого класса задач для исследования полей в континуальных непрерывных средах, например распределения потоков и гидравлических напоров при фильтрации жидкости через пористую среду, распределения напряженности электромагнитного поля в электрических машинах и т.д. Однако исторически МКЭ был разработан для решения сначала статических, а затем и динамических задач теории упругости. В данном пункте техника МКЭ будет поясняться на простом примере плоской деформации, когда в направлении, перпендикулярном анализируемому сечению, деформации отсутствуют. По мере описания метода будут делаться комментарии относительно общих особенностей МКЭ.

Итак, при исследовании напряженно-деформированного состояния деформируемый континуум, в данном случае массив горных пород разбивается на конечное число воображаемых элементов. Эти элементы связаны между собой в узлах и, в более сложных случаях, в дополнительных точках. Напряжения в анализируемом теле заменяются, таким образом, узловыми силами между взаимодействующими элементами. Перемещения узлов конечных элементов должно быть такое, чтобы минимизировать потенциальную энергию деформированного континуума. Другими словами здесь используется вариационный принцип механики.

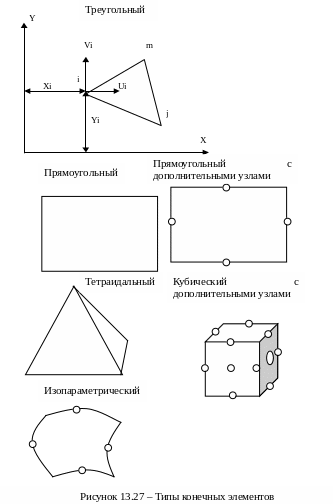
В простейшем случае используются конечные элементы треугольной формы, хотя при сложных расчетах применяют многоугольные и объемные элементы (рисунок 15.27), причем для лучшей аппроксимации объектов сложной формы пользуются элементами с криволинейными гранями. В последнем случае элементы называют параметрическими, причем для пересчета координат из прямоугольной системы в криволинейную применяют специальную процедуру.

Чтобы гарантировать сходимость решения, возможные перемещения внутри элементов должны быть специальными функциями координат в виде полиномов лагранжева или серендипова семейств. На рисунке 15.27 показан типичный треугольный элемент с узлами i, j, m. Перемещения каждого узла имеют две компоненты:

(15.41)

причем шесть компонент перемещений образуют вектор

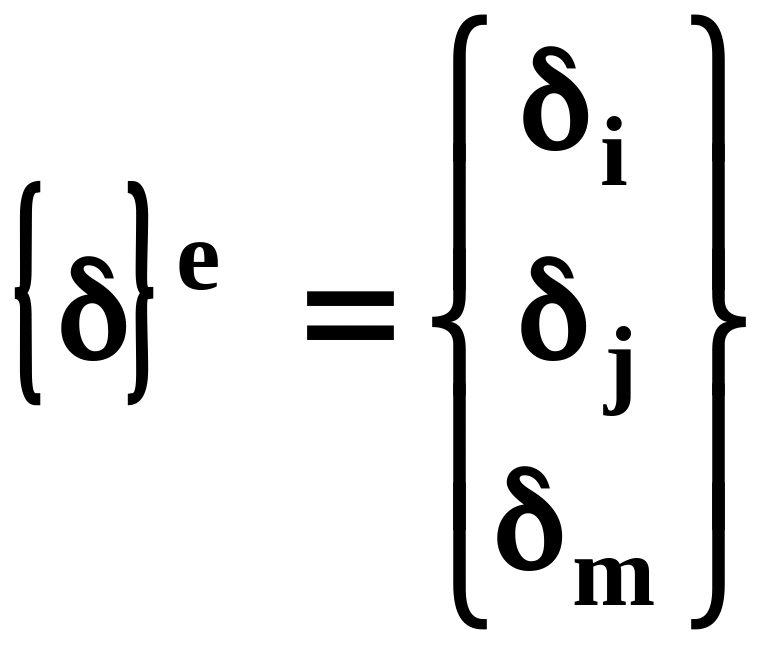(15.42)

В простейшем случае перемещения можно описать линейными полиномами

u = ₁+₂x+₃y

v = ₄+₅x+₆y (15.43)

Чем больше элемент имеет узлов, тем точнее полином и тем лучше удовлетворяется условие сплошности деформации (15.11), хотя оно всегда удовлетворяется лишь приближенно. Зная узловые перемещения, можно найти значения всех констант из следующей системы уравнений:

u_i = ₁+₂x_i+₃y_i

u_j = ₁+₂x_j+₃y_j

u_m = ₁+₂x_m+₃y_m (15.44)

Окончательно горизонтальное перемещение внутри элемента находится как

(15.45)

где

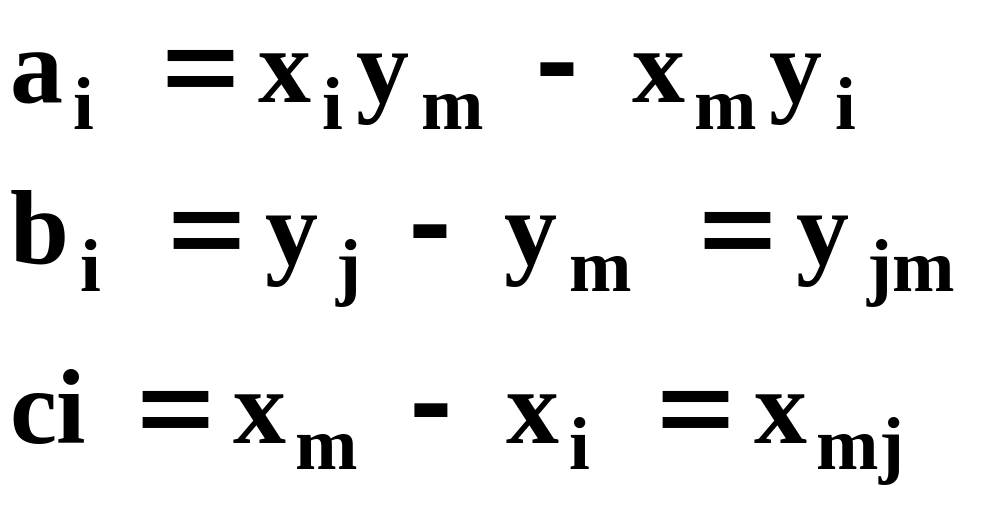
Аналогично получаем перемещение в вертикальном направлении:

(15.46)

Полную деформацию элемента характеризуем тремя компонентами:

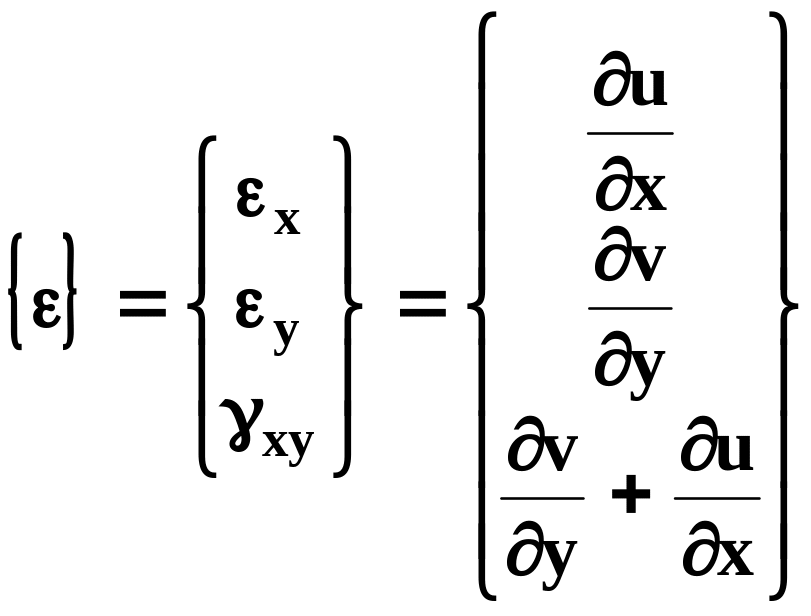(15.47)

или 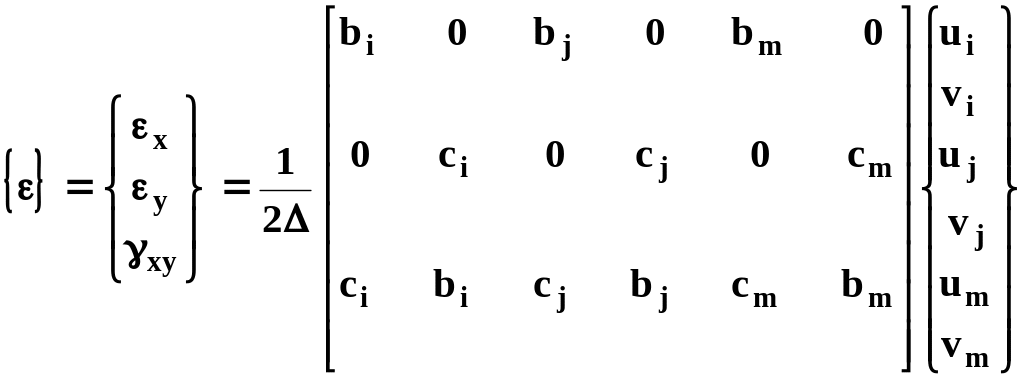(15.48)

При необходимости учитывают начальные деформации _, которые обусловлены тепловым полем, причем их вычитают из рассчитанных.

Напряжения и деформации связаны через матрицу жесткости [D]

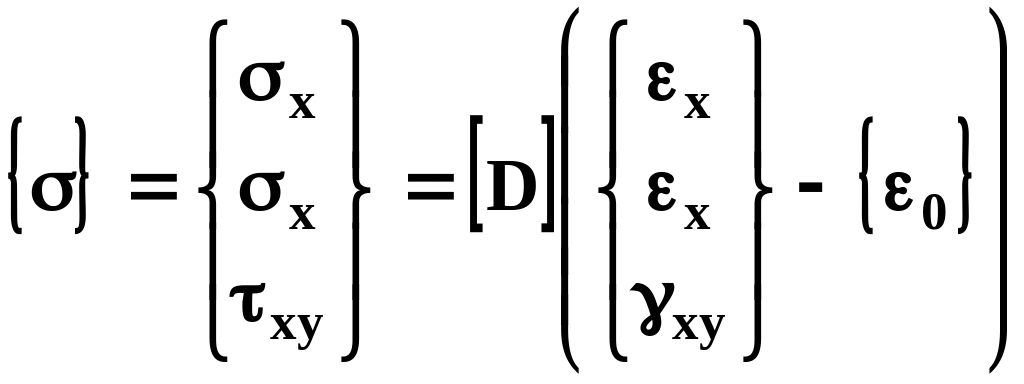(15.49)

Для плоского деформированного состояния матрица жесткости элемента имеет вид:

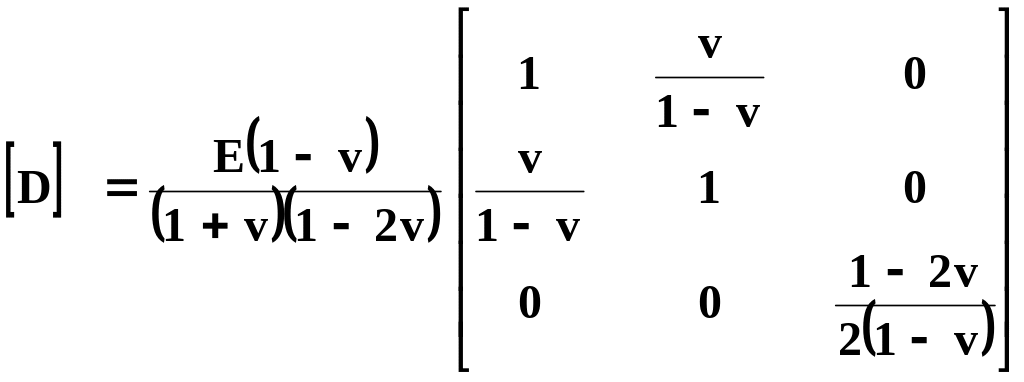(15.50)

После определения элементов матриц жесткости отдельных элементов формируется обобщенная матрица всей системы []. При этом в текущий элемент обобщенной матрицы вносят вклад жесткости всех элементов, которые примыкают к данному узлу. Затем формируется вектор сил [F], который чаще всего состоит из объемных распределенных узловых сил, определяемых весом горного массива и сил, приложенных на границе расчетной области. Неизвестные перемещения находят из решения системы линейных уравнений

[][]=[F] (15.51)

Следует отметить, что в реальных задачах число узлов расчетной области достигает нескольких тысяч и даже десятков тысяч. Поэтому матрица жесткости получается весьма больших размеров. Сама матрица имеет ленточную структуру, при которой ненулевые члены группируются в окрестности диагонали, причем лента коэффициентов жесткости симметрична. В связи с этим нужно хранить только половину коэффициентов. Несмотря на это объем данных при решении системы уравнений весьма большой и существует проблема их оперативной обработки. Для этого разработаны специальные вычислительные приемы и методы. Система уравнений решается чаще всего двумя равноценными методами: Гаусса или Холецкого, выбор которых зависит от организации структуры матрицы жесткости. Следует подчеркнуть, что формирование обобщенной матрицы жесткости и решение системы уравнений являются наиболее трудоемкими для программирования и времязатратными для компьютера операциями. После нахождения неизвестных перемещений узлов напряжения легко вычисляются по зависимостям (15.49).

В заключение отметим наиболее важные преимущества МКЭ, которые состоят в возможности имитировать элементы неоднородного горного массива, подземных выработок сложной конфигурации, крепей любой формы, достаточно легко моделировать нелинейное поведение толщи горных пород, что делает результаты расчетов ценными с практической точки зрения.

Применение метода граничных элементов для оценки напряженно-деформированного состояния массива горных пород основано на том, что напряжения и смещения внутри расчетной области получают из определенных комбинаций известных решений о распределении напряжений и смещений от усилий, заданных на границе расчетной области. Различают прямой, непрямой метод граничных элементов и метод разрывных перемещений. Сущность метода поясним сначала на примере непрямого метода граничных элементов, или как еще его именуют, метода фиктивных сил.

При методе фиктивных сил основой для решения задачи о распределении напряжений и смещений внутри расчетной области при сложных граничных условиях является известное или контрольное простое решение о распределении смещений и напряжений от силы, заданной на границе расчетной области. В качестве наиболее распространенных контрольных решений используют решение задачи Фламана о распределении смещений и напряжений в полуплоскости от приложенной на ее границе одиночной силы (рисунок 15.28), или о распределении этих же компонент в плоскости от одиночной сосредоточенной силы, приложенной в точке этой плоскости (задача Кельвина, схема которой представлена на рисунке 15.29).

Так горизонтальная, вертикальная и касательная компоненты напряжения в полуплоскости от силы, приложенной на ее границе (см. рисунок 15.28), определяются по формулам.

(15.52)

Смещения в полуплоскости, которые связаны с указанными напряжениями, находят по таким зависимостям.

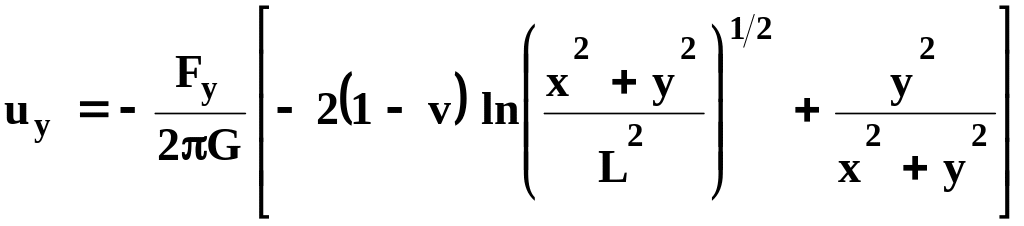(15.53)

Решение задачи о распределении напряжений и смещений в бесконечной упругой среде от действия сосредоточенной силы для условий плоской деформации в задаче Кельвина (рисунок 15.29) выражается через следующую функцию.

(15.54)

Тогда смещения записываются в виде

(15.55)

А выражения для компонент напряжения имеют вид

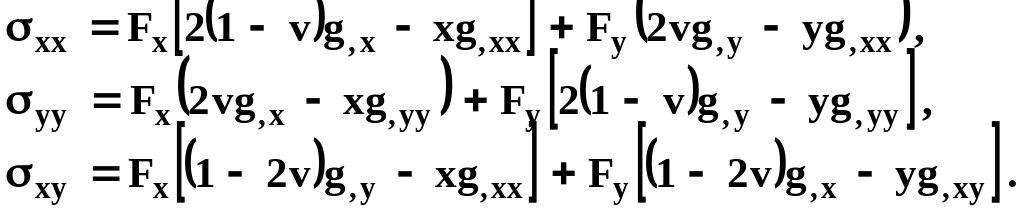(15.56)

Имея известное решение от одиночной силы, можно получить распределение напряжений и смещений от любой комбинации таких сил, приложенных на различном расстоянии от начала координат, как показано на рисунке 15.30 на примере двух сил, отстоящих от начала координат на расстоянии ξ¹ и ξ².

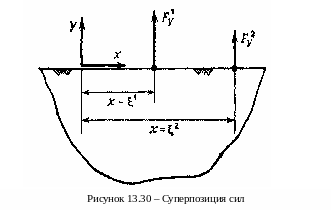
При этом используется принцип суперпозиции сил и перемещений, вызванных любым числом отдельных сил. Так вертикальная компонента перемещений, вызванная двумя вышеуказанными силами, приложенными на границе полуплоскости, вычисляется для любой точки этой полуплоскости по формуле.

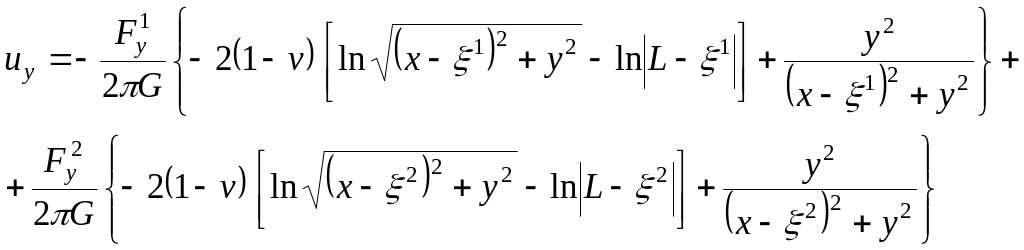(15.57)

Выражение можно записать в форме

(15.50)

где, например величина

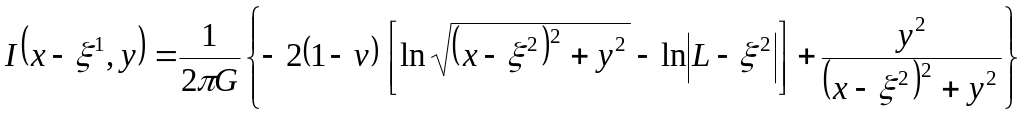(15.51)

определяет долю компоненты горизонтального смещения, вызванную действием силы F_y². Эта величина называется функцией влияния этой силы. Определение таких функций является основной задачей метода граничных элементов.

Аналогичные выражения получают для всех компонент перемещений и напряжений. Заметим, что ориентация сил на границе расчетной области в практических задачах изменяется от точки к точке. Поэтому возникает постоянная необходимость пересчета компонент сил от одной системы координат к другой. Эти пересчеты сил в разных системах координат составляют вторую рутинную задачу при реализации метода граничных элементов.

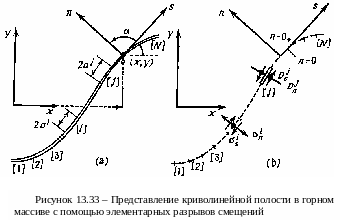
Покажем реализацию численной процедуры метода граничных элементов на примере задачи о распределении напряжений вокруг подземной полости, которая иллюстрируется на рисунке 15.31. На рисунке 15.31,а показана граница контура С подземной выработки. Обратим внимание на локальные координаты n и s, которые направлены по нормали и по касательной к кривой контура горной выработки.

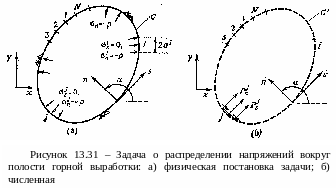
Пусть стенки полости выработки подвержены действию одинакового распределенного нормального напряжения сжатия σ_n=-p, вызванного, например действием отпора крепи и нулевых касательных напряжений σ_s. Найдем напряжения и смещения в массиве окружающих пород, вызванные этими нагрузками на границе.

Как это уже делалось при использовании метода конечных разностей, аппроксимируем контур С с помощью N отрезков, примыкающих друг к другу. Эти отрезки назовем граничными элементами. Длина одного отрезка равна 2аⁱ. Согласно принятым условиям, граничные условия будут иметь на каждом отрезке вид

(15.60)

Таким образом, физическая задача, изображенная на рисунке заменяется численной, схема которой показана на рисунке 15.31,б. Важно иметь в виду, что пунктирная кривая С¹ на рисунке уже не обозначает физическую границу выработки. В численной схеме физическая полость отсутствует, тело расчетной области является абсолютно сплошным бесконечным, а фиктивная граница С¹ лишь подобна реально существующей границе на рисунке. Решение данной задачи будем строить на основе задачи Кельвина. Приложим некоторые нормальные P_n^j и касательные Ps^j напряжения к каждому J-тому отрезку. Если такие (и теперь уже разные) напряжения будут приложены к каждому отрезку фиктивного контура, действительные напряжения, полученные на принципе суперпозиции, будут отличаться от приложенных в численной задаче. Другими словами мы должны теперь различать приложенные напряжения P_n^j , Ps^j и действительные σ_n , σ_s , которые мы собираемся найти по методу суперпозиции, описанному выше.

После преобразования координат и нахождения функций влияния получим систему уравнений

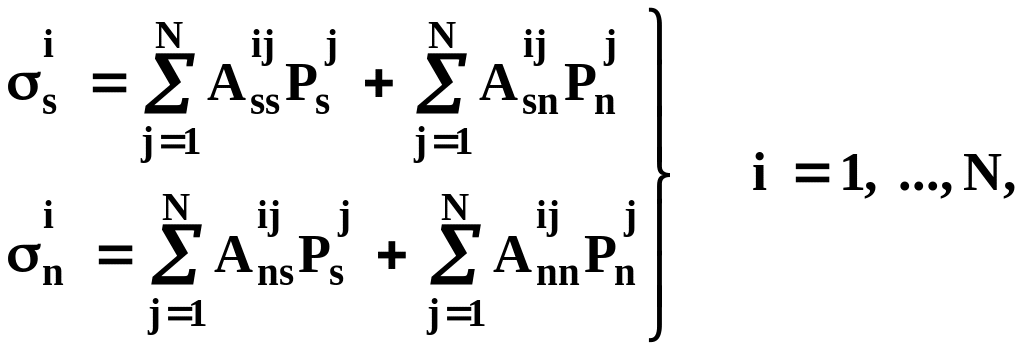(15.61)

Коэффициент A^ij_sn например, дает действительное касательное напряжение σ_s в центре i-того отрезка, вызванное постоянной единичной нормальной нагрузкой P_n, приложенной в центре j-того отрезка.

Если нам теперь удастся найти такие значения приложенных (фиктивных) напряжений P_n^j , Ps^j для всех аппроксимирующих отрезков фиктивного контура, что действительные напряжения σ_n , σ_s окажутся равными (примерно с заданной наперед точностью) значениям, заданным условием (15.60), то мы получим приближенное решение физической задачи, изображенной на рисунке 15.31,а. Технически это означает, что мы должны решить систему линейных алгебраических уравнений.

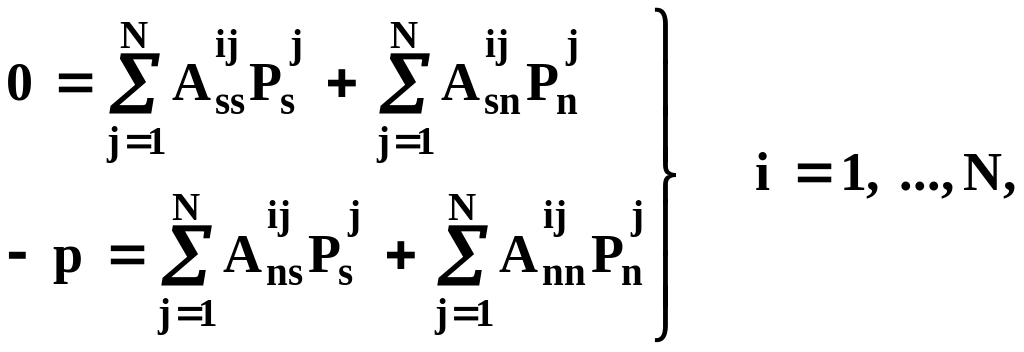(15.62)

Описанный метод и называется методом фиктивных сил, поскольку прилагаемые напряжения не являются в полном смысле реальными, действующими на контуре выработки.

К методу фиктивных сил тесно примыкает метод граничных интегралов. При его применении составляется очень похожая система линейных уравнений. Отличием является то, что неизвестные граничные смещения и напряжения находятся прямо по заданным граничным условиям.

Часто практические задачи геомеханики связаны с определением напряженно-деформированного состояния в окрестности щелеподобных вырезов или трещин. Типичными примерами являются поля напряжений и деформаций вокруг выработанных пространств, образованных длинными очистными забоями. Метод фиктивных нагрузок непригоден для решения таких задач, поскольку влияние граничных элементов, принадлежащих плоскости кровли неотличимо от влияния элементов противоположной поверхности, в данном случае почвы. Для решения подобных задач применяют другой вариант метода граничных элементов, именуемый методом разрывных смещений. Этот метод основан на аналитическом решении задачи о бесконечной плоскости, смещения в которой терпят постоянный по величине разрыв в пределах конечного отрезка.

Процедура реализации метода разрывных перемещений напоминает ту, которую описывали в предыдущем пункте. Трещину или выработанное пространство разбивают на N граничных элементов и в пределах каждого элемента разрывы считаем постоянными. Заметим при этом, что мы заранее должны знать готовое решение о распределении напряжений и смещений от элементарного разрывного смещения точно так же, как мы знали готовое стандартное решение о распределении напряжений от силы, приложенной на границе полуплоскости или в точке бесконечной плоскости. Поэтому, зная аналитическое решение для одного постоянного разрыва смещений и суммируя влияния всех N элементов, находим численное решение задачи от произвольно распределенных разрывов на границе расчетной плоской полости или выработанного пространства.

В таких практических задачах, как нахождение напряжений вокруг выработанного пространства, распределение разрывов смещений на контуре этого пространства заранее неизвестны. Зато известны усилия или напряжения на контуре такого пространства. В частности, если кровля еще не обрушилась, напряжения на контуре выработанного пространства равны нулю или отпору крепи. В таком случае можно отыскать значения элементарных разрывов на отдельных отрезках граничных элементов, которые необходимы, чтобы вызвать такие усилия или напряжения. Это достигается аналогичным и уже известным для нас путем решения системы алгебраических уравнений.

Еще раз подчеркнем, что методически процедура разрывных перемещений реализуется так же, как и метод фиктивных сил. Для этого используется, как уже говорилось выше, готовое аналитическое решение о смещениях и напряжениях вокруг элементарного разрыва смещений на конечном отрезке плоскости. Это решение получено Краучем С. и выглядит следующим образом. В бесконечной упругой среде задают на отрезке длиной 2а разрыв смещений постоянной величины D_i. Отрезок разрыва ориентируют вдоль оси x как показано на рисунке 15.32.

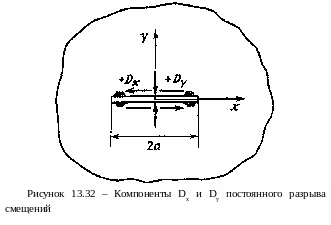
Рассматривая разрыв как трещину, можно выделить две поверхности, одна из которых лежит на положительной стороне вертикальной оси y=0₊ , а другая на отрицательной y=0_-. При переходе с одной стороны отрезка на другую смещения испытывают постоянное заданное изменение, состоящее из двух компонент: D_i=(D_x, D_y).

По определению разрыв смещений определяется как разность смещений двух сторон отрезка

(15.63)

или

(15.64)

Смещения и напряжения в любой точке плоскости от такого разрыва определяются формулами Крауча

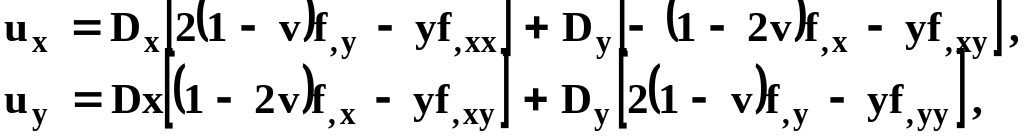(15.65)

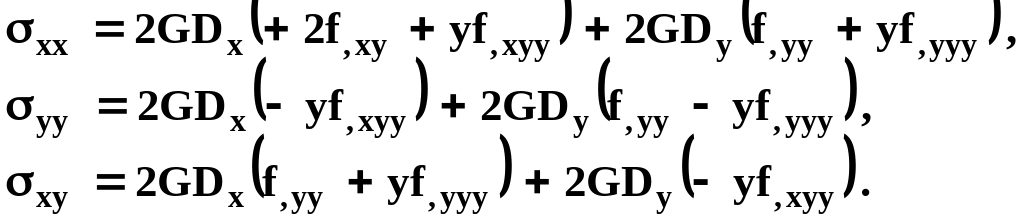(15.66)

где модуль G сдвига. Функция f_x,y имеет вид.

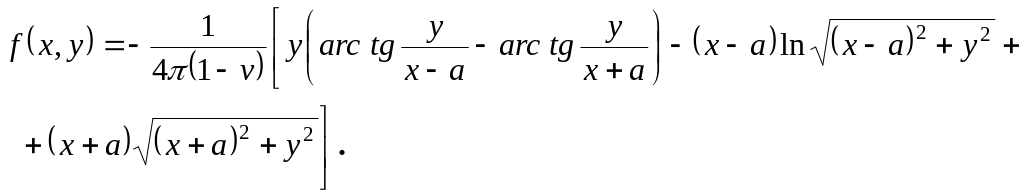(15.67)

Производные третьего порядка от этой функции выражаются формулами

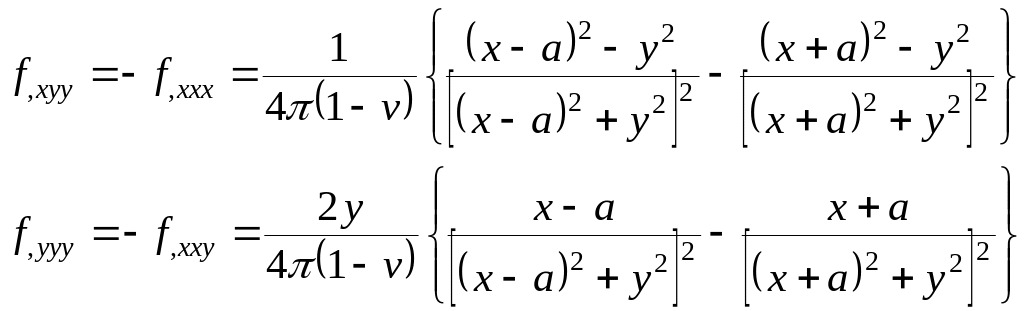(15.68)

Теперь имея аналитическое решение о распределении напряжений и смещений вокруг элементарного разрыва, можно найти распределение напряжений и смещений вокруг разрыва произвольной формы (трещины, выработанного пространства и т.п.), аппроксимировав его набором элементарных прямолинейных разрывов, как показано на рисунке 15.33.

Касательные и нормальные компоненты разрывных перемещений на j–том элементе рисунка 15.33,б определяются следующим образом

(15.69)

При этом знаками + и – обозначены положительная и отрицательная поверхности трещины по отношению к оси n локальных координат.

Влияние отдельного элементарного разрыва смещения на смещения и напряжения произвольной точки бесконечного твердого тела можно определить из системы

(15.70)

Коэффициент A^ij_ns дает нормальное напряжение σⁱ_n в центре i-того элемента, вызванное постоянным единичным разрывом смещения D^j_s=1 в касательном направлении вдоль j–того элемента. По известным напряжениям на границах разрыва и единичным величинам разрывов находят коэффициенты влияния А.

Компоненты напряжений от всех элементарных разрывов связаны с соответствующими разрывами системой уравнений

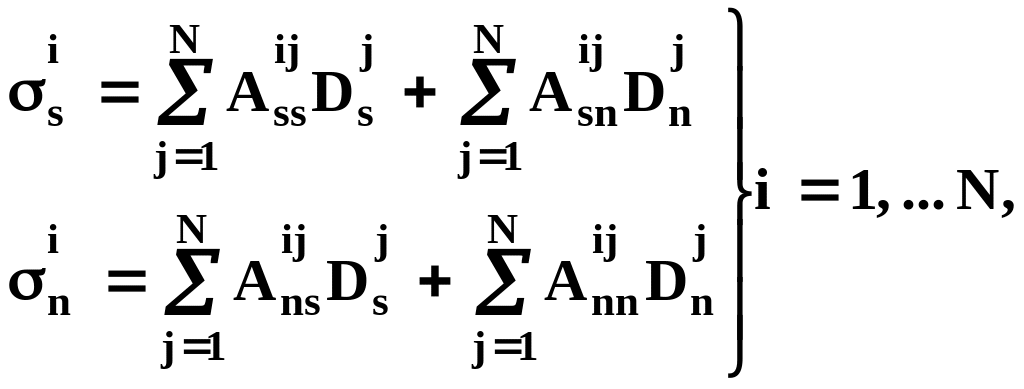(15.71)

В результате решения этой системы находят неизвестные компоненты элементарных разрывов смещений вдоль всей границы реального разрыва, заданного в задаче. Теперь используя известные решения для компонентов D , можно на основе принципа суперпозиции определять смещения и напряжения в произвольной точке массива вокруг заданного разрыва произвольной формы (то есть выработанного пространства или трещины в данном случае).

Нелинейность деформирования горного массива следует рассматривать на нескольких уровнях. На первом уровне рассмотрим упругое, то есть линейное поведение массива, которое примем в качестве эталонного для дальнейшего сравнения. На графике зависимости напряжений от деформаций (рисунок 15.34) этот уровень или этап деформирования выделен интервалом 1. Характерно, что на этом этапе деформационная характеристика горного массива совпадает с касательной. Важно, что движение по характеристике вверх, то есть в сторону увеличения напряжений и вниз в сторону разгрузки от напряжений обратимо, или осуществляется по одной и той же наклонной линии. Типичным примером упругого деформирования массива является его сжатие в зоне опорного давления, а также разгрузка под выработанным пространством в процессе надработки.

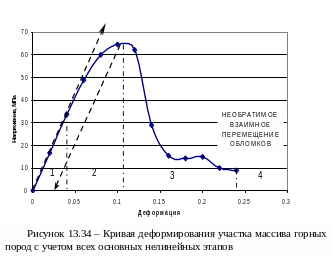
На втором этапе деформационная характеристика породы начинает отличаться от линейной, хотя с ростом деформации напряжения продолжают также увеличиваться. На этом и последующих нелинейных этапах процесс деформирования становится необратимым. Это значит, что разгрузка породы происходит по другой линии, не совпадающей с нагрузочной ветвью деформационной характеристики, как показано на рисунке 15.32. При этом наблюдается остаточная пластическая деформация материала породы. Характерным примером пластической деформации горных пород можно считать пучение глинистых пород почвы штрека в зоне опорного давления движущейся лавы. Для описания такого рода деформаций применяется специальная теория пластичности, которая является развитием теории упругости.

На третьем этапе деформирования породы происходит резкое уменьшение напряжений при продолжающейся ее деформации. Этот этап называют запредельным, так как происходит исчерпание предела прочности породы. Типичным примером запредельного деформирования массива является отжим краевой части пласта.

Последним характерным этапом условного деформирования массива после его разрушения можно считать необратимое взаимное перемещение обломков. Такое перемещение происходит при обрушении кровли, перемещении закладки в выработанное пространство, уплотнении обрушенных пород и т.д. Важно отметить, что при решении практических задач горного дела четвертый этап перемещения обломков или частиц пород часто рассматривается как продолжение процесса необратимого деформирования массива в целом.

Еще одним специфическим нелинейным деформированием обладают породы, склонные к ползучести во времени под действием постоянной нагрузки (рисунок 15.35). Наиболее типичным примером временнόй ползучести горного массива является деформирование камер и потолочин месторождений соли без разрушения их сплошности.

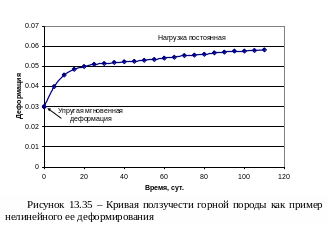
Важно отметить, что в очень большом диапазоне горно-геологических условий имеют место все четыре этапа деформирования плюс временнáя ползучесть, причем часто эти процессы происходят одновременно. Это характеризует массив горных пород как очень сложный геомеханический объект, для описания которого необходимо привлекать все современные методы деформируемого тела. Этим горный массив принципиально отличается от других объектов. Так подавляющее большинство конструкций и сооружений рассчитывают только до предела упругости. Никого не интересует, как будут разлетаться обломки самолета после разрушения его корпуса от перегрузок. Важно не допустить процесс деформирования за пределы упругости и тем более прочности. То же касается расчета автомобильного демпфера, который должен работать как на упругом участке деформирования, так и на пластическом (втором участке). Однако после полного разрушения и разлета на куски (третий и четвертый этапы деформирования) демпфер перестает выполнять свои функции. В отличие от вышесказанного, все этапы деформирования горного массива являются равными по значимости и одинаково важны в общей технологической цепочке добычи полезного ископаемого. Именно этим обстоятельством объясняется большое разнообразие методов, применяемых при анализе напряженно-деформированного состояния массива горных пород.

Следует отметить, что большинство нелинейных методов механики деформируемого тела основаны на вышеописанном алгоритме, который разработан для упругого механизма деформирования. Учет нелинейности осуществляется за счет искусственных приемов, некоторые из них описываются далее.

Основой для учета нелинейного деформирования массива горных пород является его деформационная характеристика. Нелинейность деформирования массива на этапах 2 и 3 имитируют путем многократного или пошагового расчета напряженно-деформированного состояния при изменении модуля деформации рассматриваемого массива. На рисунке 15.36 показан прием учета нелинейности деформирования, основанный на переменном модуле деформации.

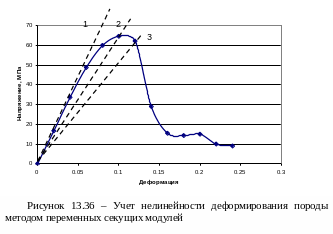
Смысл такого приема заключается в следующем. На начальном этапе расчета определяют напряжения и деформации во всех расчетных точках модели. Затем проверяют адекватность величин напряжений и деформаций по экспериментальной (или априорно заданной) деформационной кривой. В тех точках расчетной области, где соотношения между напряжениями и деформациями не ложатся на экспериментальную деформационную кривую, изменяют (как правило, уменьшают) модуль деформации таким образом, чтобы полученные напряжения соответствовали деформациям и пересчитывают все распределение напряжений в модели заново. В процессе приведения напряжений и деформаций в экспериментально установленное соответствие приходится заменять отрезок деформационной кривой прямым отрезком, который пересекает ее в точке, где наблюдается соответствие напряжений и деформаций. По этой причине такой подход получил название метода секущих модулей. Недостатком такого метода является необходимость пересчета всей матрицы жесткости в случае использования метода конечных элементов, что увеличивает время расчета. При применении других методов расчета необходимо пересчитывать характеристики, аналогичные тем, которые составляют матрицу жесткости в МКЭ. Кроме того, сходимость решения получить удается не всегда. Другими словами при каждом новом пересчете напряженного состояния модели расхождение между напряжениями и деформациями в тех точках, где предел упругости был превышен, не только не уменьшается, но часто и растет.

Б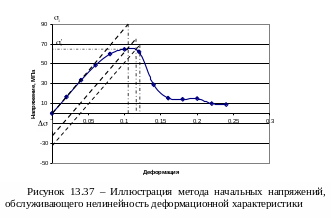 олее эффективный прием учета нелинейного деформирования массива на этапах 2 и 3 показан на рисунке 15.37.

При обнаружении точки модели, где расчетные напряжения и деформации не ложатся на экспериментальную кривую деформирования вводят поправки в вектор узловых сил, имеющих обратный невязке знак. Например, невязка напряжений составила ∆σ=σ₁-σ₁¹. В узел, где обнаружена такая невязка, вводят компоненты сил, пропорциональные полученной невязке с обратным знаком и тем самым приводят в соответствие величины напряжений и деформаций согласно экспериментальной нелинейной зависимости. Такой подход назван методом начальных напряжений. Поскольку такая корректировка производится в нескольких узлах сразу, сходимость решения достигается постепенно, в течение несколько итераций. Важно, что при этом матрица жесткости не пересчитывается, что ускоряет время решения задачи.

Существует большое количество приемов для учета нелинейного деформирования среды. Однако следует оговориться, что для моделирования процессов, протекающих на всех этапах, включая четвертый, необходимо применение принципиально иных методов, о которых будет сказано далее.