3.1.3. Операторный метод расчета переходных процессов.

Анализ переходных процессов даже для относительно простых цепей зачастую представляет значительные сложности, т.к. требует решения дифференциальных уравнений. Задачу можно существенно упростить, если преобразовать уравнения, сделав их алгебраическими. Но в переходных процессах во всех функциях переменной величиной является время, поэтому для исключения производных требуется перейти к новой не зависящей от времени переменной. Такой переход для функции f(t) можно осуществить, например, с помощью преобразования Лапласа

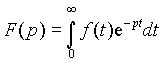
(3.10)

где p = a + jb - некоторое комплексное число, являющееся переменной функции F(p).

Функция времени f(t) называется оригиналом, а функция комплексной переменной F(p) - ее изображением.

Обратный переход от изображения к оригиналу может быть осуществлен с помощью обратного преобразования Лапласа

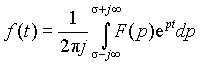
(3.11)

Для большинства функций встречающихся в практических задачах существуют таблицы прямого и обратного преобразований и необходимость применения выражений (1) и (2) возникает крайне редко. Простейшие из этих преобразований приведены в таблице 1.

3.1.3.1.Свойства преобразования Лапласа:

1). Теорема суперпозиции. Изображение суммы равно сумме изображений слагаемых.

2). Теорема линейности. Изображение произведения функции на постоянную величину равно произведению изображения функции на эту постоянную.

.

АЭП. 3.1.14. 05.08.11.

3. Теорема интегрирования: Изображение интеграла функции.

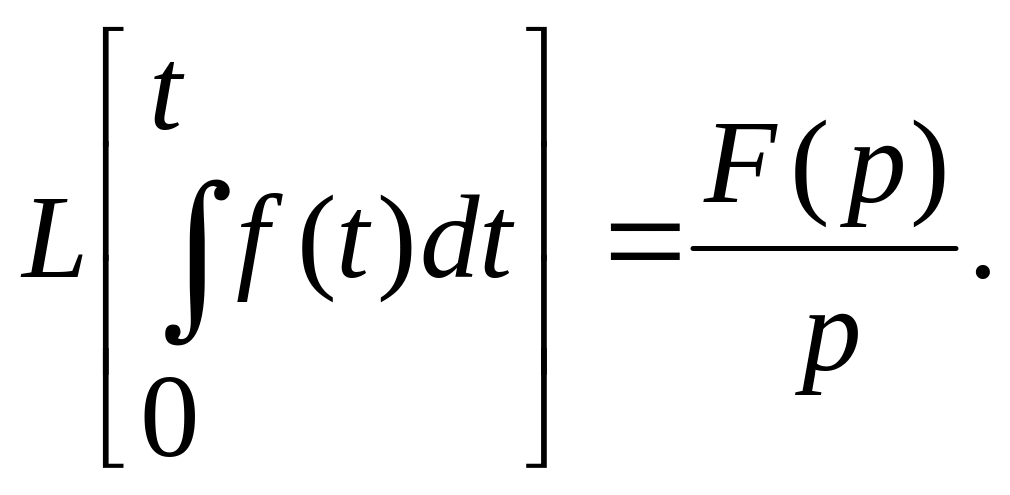
4. Теорема дифференцирования:

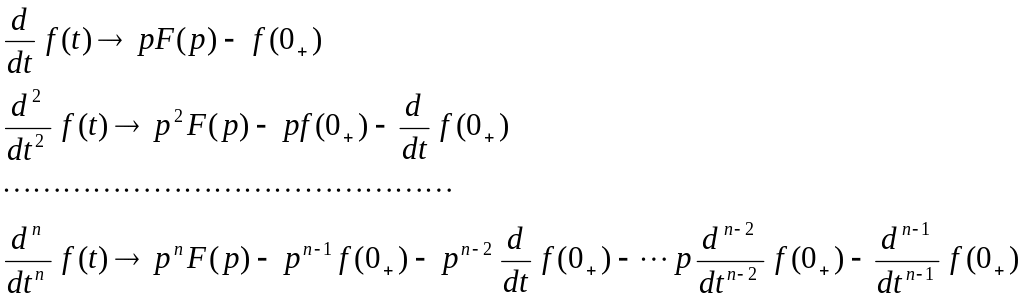
5). Теорема смещения в вещественной области

(Теорема запаздывания).

Если оригинал смещается вдоль оси t на постоянную и при ,

6). Теорема смещения в комплексной области.

7.) Теорема умножения изображения изображений (теорема свёртки в вещественной области).

Пусть

тогда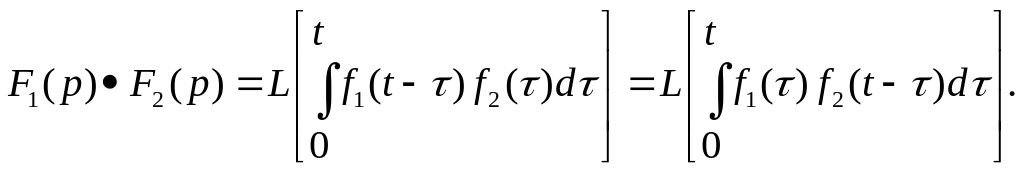

Интегралы в правой части называют сверткой функций. Произведение изображений соответствует свертке оригиналов. Свертка двух функций соответствует произведению их изображений.

8.) Теорема подобия(изменение масштаба).

Где а=const.

АЭП. 3.1.15. 05.08.11.

9). Теорема о конечном значении (по Лапласу) .

10). Теорема о начальном значении.

Изображения некоторых функций приведено в таблице.

Оригинал	Изображение
1(t)	1/p
A*1(t)	A/p
(t)	1
A*(t)	A
A	A/p
A*e-*t	A/(p+)
1- e-*t	/ [p*(p+)]
A * (1- e-*t)	A*/ [p*(p+)]
A * cos(*t)	A *p / (p2 + 2)
A*sin(*t)	A * / (p2 + 2)
t	1/p2
cos(*t)	p/(p2+2)
sin(*t)	/(p2+2)

3.1.3.2. Законы Кирхгофа в операторной форме. [Сергеев в.В.]

Первый закон Кирхгофа: алгебраическая сумма токов ветвей сходящихся в узле в любой момент времени равна нулю

()

Преобразуем по Лапласу обе части этого равенства, учитывая свойство линейности (3.2). Тогда получим первый закон Кирхгофа в операторной форме

АЭП. 3.1.16. 05.08.11.

Его формулировка: алгебраическая сумма операторных токов ветвей, сходящихся в узле, равна нулю.

Второй закон Кирхгофа: алгебраическая сумма напряжений на ветвях замкнутого контура в любой момент времени равна нулю

На основании свойства линейности после преобразования по Лапласу этого равенства получим второй закон Кирхгофа в операторной форме

Его формулировка: алгебраическая сумма операторных напряжений на ветвях замкнутого контура равна нулю.