2. Кривая разгона двигателя.

Рисунок 3.2.4.

3.2.6. Cинтез переходного процесса.

Заданы тахограмма процесса, n=f(t) и механическая характеристика машины и момент инерции привода.

Требуется определить требуемый момент электродвигателя для реализации заданного процесса.

АЭП. 3.2.7. 18.09.05.

Рассмотрим синтез переходного процесса на примере.

n

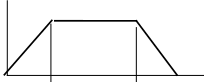
t

M

t

Рисунок 3.16.

Момент двигателя при пуске:

М = Мдин+ Мс = J * dω/dt + Мс

так как dω/dt = const то:

Мдин = J / * ωн / tп = J /9.55 * nн /tп

т.к. ω = 2 * π * n /60 = n /9.55

2. Момент при установившейся скорости:

М = Мс

т.к. dω/dt = 0 и Мдин = 0

3. Момент при торможении:

М = Мдин - Мс

где: Мдин = J / * ωн / tп = J /9.55 * nн /tп

АЭП. 3.2.8. 18.09.05.

4.5. Двухмассовая механическая система.

2.1 Общие сведения

Состояние реальной динамической системы редко может быть описано только одной переменной, поскольку реальная система, как правило, представлена несколькими компонентами, состояние каждого из которых описывается своей переменной. Подобные системы называются динамическими системами n-го порядка. Их поведение, соответственно, описывается системой из n дифференциальных уравнений или одним уравнением n-го порядка. Моделирование таких систем в значительной мере облегчается, если воспользоваться матричной формой записи уравнений состояния, применив по отношению к ней известные численные методы решения.

Ниже на примере анализа двухмассовой ЭМС рассматривается случай идентификации и моделирования динамической системы 3-го порядка.

Поведение двухмассовой ЭМС описывается следующими математическими соотношениями.

Наличие механической связи, характеризуемой небесконечной жесткостью, между двумя массами системы обуславливает появление сил упругого взаимодействия между ними. После дифференцирования исходного уравнения, составляемого по закону Гука, получим:

(2.1)

где ₁, ₂ – частоты вращения первой и второй масс;

с₁₂ – коэффициент жесткости упругой механической связи между массами;

М₁₂ – момент упругости.

Для каждой массы, входящей в систему, справедливо уравнение равновесия сил, которое при отсутствии внешних воздействий на промежуточные массы системы имеет вид.

(2.2)

где J₁, J₂ – моменты инерции первой и второй масс;

М – момент, развиваемый двигателем, входящим в состав первой массы;

М_с=М_с(t,φ₂,ω₂) – статический момент сопротивления, воздействующий на вторую массу системы.

Электромеханическую связь между механическими координатами первой массы, в состав которой входит электромеханический преобразователь (двигатель), в первом приближении (если не учитывать инерционность электромагнитных процессов в двигателе) описывается соотношением:

(2.3)

где β – жесткость механической характеристики двигателя;

₀ – частота вращения холостого хода.

АЭП. 3.2.9. 18.09.05.

Влияние механической нагрузки учитывается зависимостью М_с(t,φ₂,ω₂) статического момента сопротивления, воздействующего на вторую массу, от времени, частоты вращения или угла поворота (табл.1.1).

Таким образом, полное математическое описание двухмассовой ЭМС будет представлено тремя дифференциальными (2.1) – (2.2) и двумя алгебраическими уравнениями.

Матричное представление уравнений состояния позволяет существенно упростить решение. В данном случае матричная форма записи уравнений состояния и уравнений связи динамической системы имеет вид:

(2.4)

где 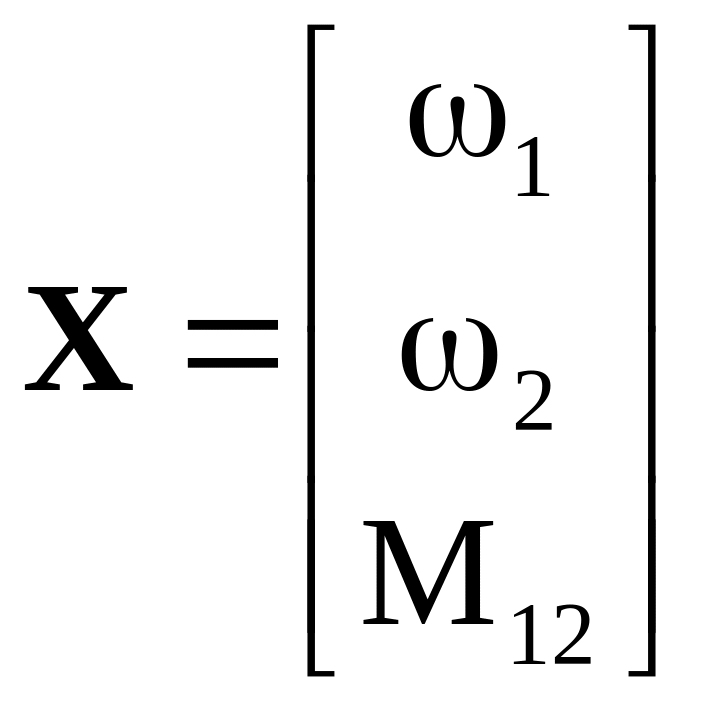- вектор переменных состояния исследуемой ЭМС,

- вектор внешних воздействий на ЭМС,

- вектор наблюдаемых величин,

A, B, C, D - матричные коэффициенты:

, , ,

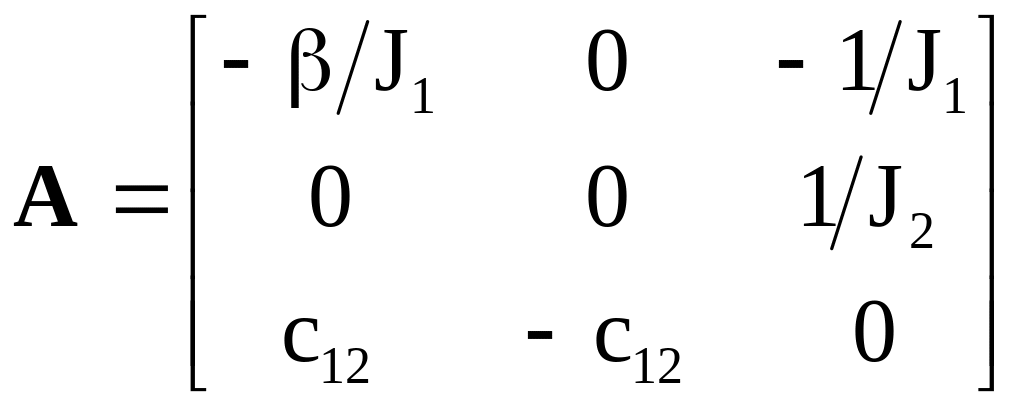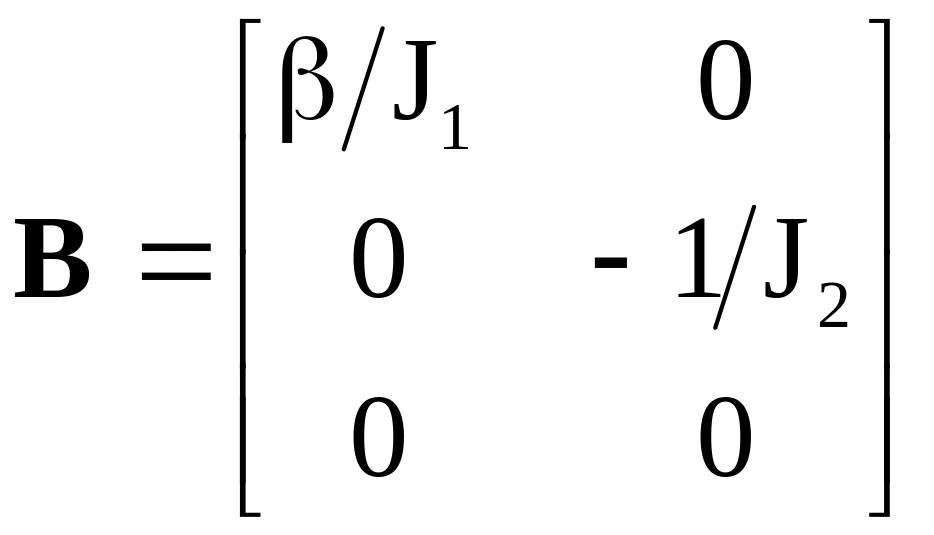В случае численного решения уравнения (2.4) для получения результата, характеризуемого приемлемой точностью, следует правильно выбрать шаг интегрирования t_и, величина которого определяется наименьшей постоянной времени Т_min. Целесообразно при выборе шага интегрирования руководствоваться соотношением (2.5):

t_и=(0.01…0.05)Т_min. (2.5)

Т_min определяется как минимальная величина из трех постоянных времени Т₁, Т₂, Т₃. Последние могут быть определены в результате решения характеристического уравнения (2.6), соответствующего дифференциальному уравнению состояния (2.4):

(2.6)

где I – диагональная единичная матрица с размерностью, соответствующей размерности матричного коэффициента А (3*3);

k – корень (корни) характеристического уравнения.

Зная корни k_i (в общем случае, комплексные) характеристического уравнения, можно определить i-ую постоянную Т_i, воспользовавшись соотношением:

(2.7)

АЭП. 3.2.10. 18.09.05.