Практическое задание.

Задача №17

При определении состава сжатого воздуха, предназначенного для заполнения баллонов дыхательного аппарата, путем многократных измерений получили следующие данные по содержанию кислорода (%): 20,5; 21,3; 21,9; 22,1; 21,5; 20,9; 21,1; 22,0; 21,0.

Записать результат измерения содержания кислорода в сжатом воздухе (О₂), если принятая доверительная вероятность Р=0,99 и коэффициент Стьюдента t_р=3,33.

Решение.

1. Найдём среднее арифметическое значение результатов измерений:

2. Найдём стандартное отклонение:

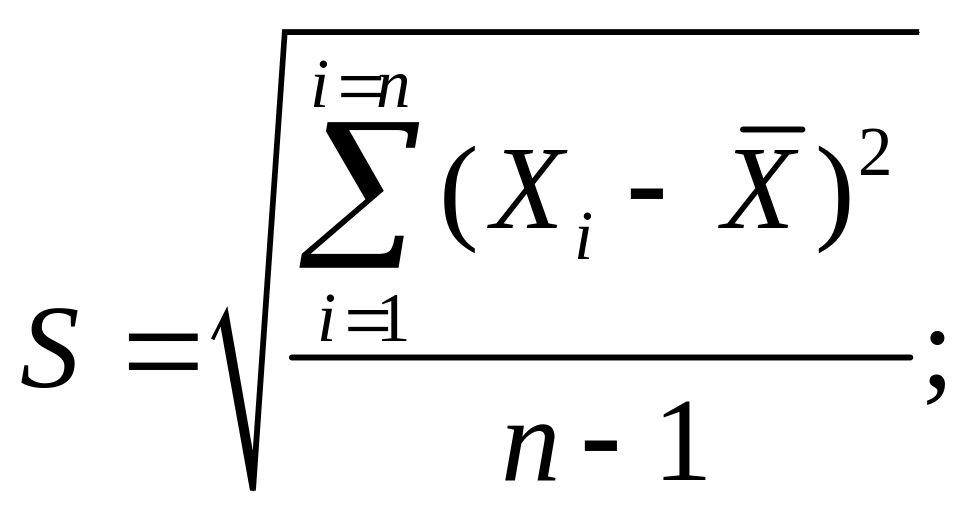
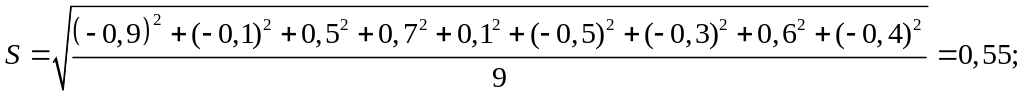
3.Найдём случайную погрешность измерения:

Ответ. Результат измерения

Задача №22

При многократном измерении напряжения электрического тока в цепи среднее арифметическое показаний вольтметра Ū= 127В. Погрешность от подключения вольтметра в цепь (изменение напряжения) равна –1,2В. Стандартное отклонение S=1,58.

Чему равно действительное значение напряжения в цепи, если принятая доверительная вероятность Р=0,95 и коэффициент Стьюдента t_р=2,00?

Решение.

1. Найдём измеренное среднее арифметическое показание вольтметра:

2. Найдём случайную погрешность измерения:

При p=0,95 и t_s=2,00 => n=21;

3. Найдём действительное значение в цепи:

Ответ. Действительное значение в цепи

Задача №45

При измерении некоторой физической величины получили следующие результаты (см. свой вариант). По данным измерений постройте гистограмму и по внешнему виду гистограммы сделайте вывод о принадлежности распределения результатов наблюдений нормальному закону распределения. Используйте критерий согласия Пирсона для проверки высказанного теоретического предположения.

Даны 120 независимых равноточных измерений некоторой физической величины:

7,83	7,81	8,22	7,24	8,22	7,26	8,15	8,09	7,32	8,20
7,77	8,27	8,75	8,70	8,79	7,60	7,74	7,87	8,11	7,91
8,00	7,96	8,29	7,94	7,54	7,97	7,78	8,04	8,20	8,48
7,77	8,30	8,79	8,86	7,78	8,02	8,57	8,00	8,13	7,81
7,78	7,55	8,16	8,06	8,07	7,81	7,79	7,39	8,31	8,09
8,17	8,72	7,95	7,83	8,49	8,19	9,08	8,02	7,83	8,24
8,21	8,59	8,19	8,06	8,26	8,01	7,85	7,49	7,62	8,40
8,53	8,29	8,24	8,89	7,73	8,62	8,02	7,34	8,24	8,08
7,68	8,60	7,95	8,40	7,42	7,99	7,79	7,83	8,44	7,80
8,29	8,21	7,97	7,68	7,73	7,93	7,98	7,81	8,29	8,57
7,89	8,60	7,56	8,41	8,51	8,05	8,28	9,15	7,15	7,66
7,97	7,70	8,34	8,46	7,91	7,64	8,37	7,99	7,97	8,28

Рассчитать:

1. При уровне значимости 0,05 исследовать предложенную выборку на однородность. Исключить все грубые ошибки с вероятностью 1–q. Найти среднее значение и эмпирический стандарт S полученной однородной выборки.

2. Сгруппировать однородную выборку по интервалам, построить гистограмму относительных частот, сформировать гипотезу о виде распределения случайной величины Х.

3. Проверить гистограмму о распределении величины Х по критерию согласия Пирсона, установить вероятность р, с которой высказанная гипотеза не согласуется с истинным распределением. Если р<0,50, то данную гипотезу не отвергать, остановиться на данном виде распределения и перейти к пункту 4. Если р>0,50, то выбрать другой закон распределения и снова применить к нему критерий согласия Пирсона. Если при исследовании гипотез о трех различных распределениях (нормальном, логарифмическом и распределении Вейбулла) вероятность несогласования р>0,50, то выбрать лучшее по вероятности распределения.

4. Найти доверительный интервал для математического ожидания M(X)=m и среднего квадратичного отклонения (X)=, если задан уровень значимости q, полученной в пункте 3 при выборе распределения величины Х.

Решение:

1. Исследуем данную выборку на однородность. Для этого все результаты измерений расположим в порядке возрастания. Результат запишем в виде табл. 61.

По условию требуется проверить, не содержит ли данная выборка грубых ошибок на уровне значимости 0,05, то есть из выборки следует исключить те х_i, которые с вероятностью 1–q=0,95.

Найдем критическое значение числа

,

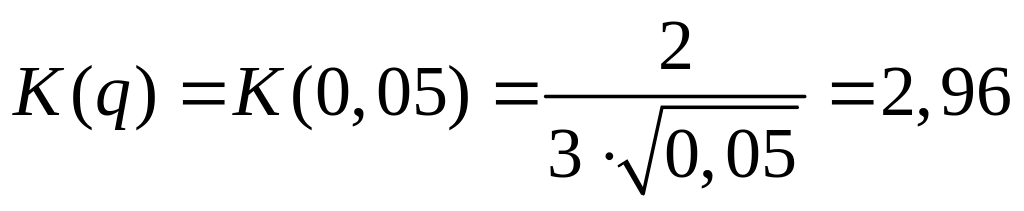с которым будем сравнивать максимальное отклонение t(x_i). Нанесем на ось все значения из табл. 6.1.

Табл. 6.1. Экспериментальные значения величины Х

I	xi	i	xi	i	xi	i	xi
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30	7,15 7,24 7,26 7,32 7,34 7,39 7,42 7,49 7,54 7,55 7,56 7,6 7,62 7,64 7,66 7,68 7,68 7,7 7,73 7,73 7,74 7,77 7,77 7,78 7,78 7,78 7,79 7,79 7,8 7,81	31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60	7,81 7,81 7,81 7,83 7,83 7,83 7,83 7,85 7,87 7,89 7,91 7,91 7,93 7,94 7,95 7,95 7,96 7,97 7,97 7,97 7,97 7,98 7,99 7,99 8 8 8,01 8,02 8,02 8,02	61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90	8,04 8,05 8,06 8,06 8,07 8,08 8,09 8,09 8,11 8,13 8,15 8,16 8,17 8,19 8,19 8,2 8,2 8,21 8,21 8,22 8,22 8,24 8,24 8,24 8,26 8,27 8,28 8,28 8,29 8,29	91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120	8,29 8,29 8,3 8,31 8,34 8,37 8,4 8,4 8,41 8,44 8,46 8,48 8,49 8,51 8,53 8,57 8,57 8,59 8,6 8,6 8,62 8,7 8,72 8,75 8,79 8,79 8,86 8,89 9,08 9,15

Рис. 6.1. Распределение случайной величины

Как можно видеть из рис. 6.1, наиболее густо точки расположены в интервале [7,56, 8,62]. Значение x₁=7,15 резко отличается от интервала [7,56, 8,62], что может служить косвенным подтверждением того, что величина x₁ является грубой ошибкой. Остальные значения x_i не вызывают особых подозрений, поэтому мы исследуем дополнительно крайние точки x₁, x₂, x₁₁₉ и x₁₂₀.

Временно отбросив указанные значения, подсчитаем среднее арифметическое значение и эмпирический стандарт:

;

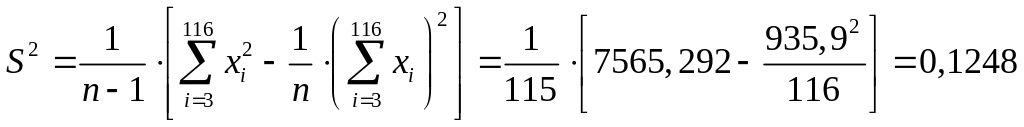и .

Исследуем сначала x₁=7,15, применив к нему наш критерий. Оказалось, что 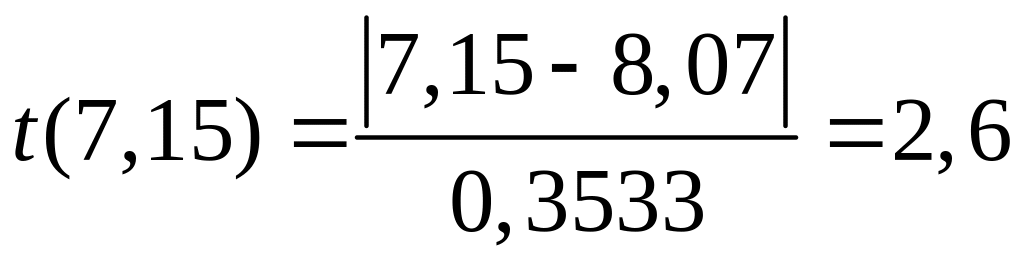. Так как , то значение x₁=7,15 не является грубой ошибкой, и поэтому данное значение должно быть включено в результаты обработки, следовательно, значение x₂=7,24 тоже должно быть включено в результаты обработки.

Включив в выборку x₁=7,15 и x₂=7,24, пересчитаем с учетом их и .

Получим

;

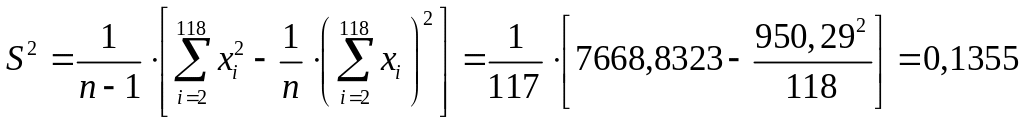и .

Вычислим 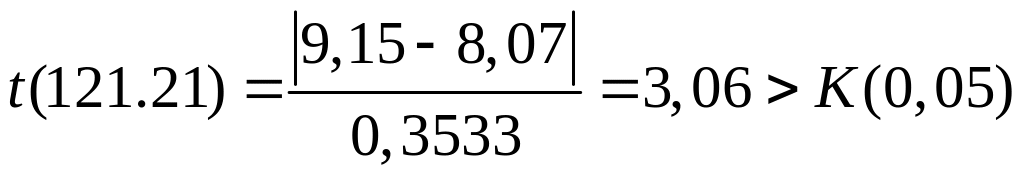. Следовательно, x₁₂₀=7,15 является грубой ошибкой, и поэтому данное значение должно быть исключено из результатов обработки.

Вычислим 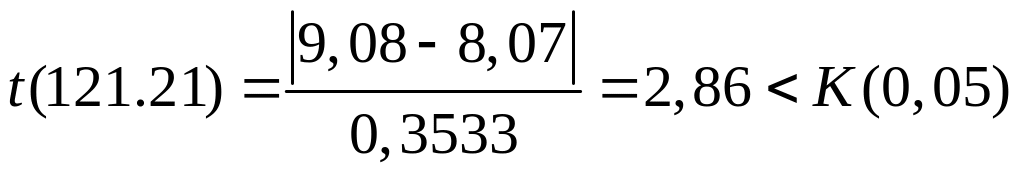. Таким образом, значение x₁₁₉=9,08 также принадлежат к выборке, поэтому включаем его в выборку и с вероятностью 1–р=0,95 выборка, представленная в табл. 6.1, является однородной.

Для полученной выборки находим

;

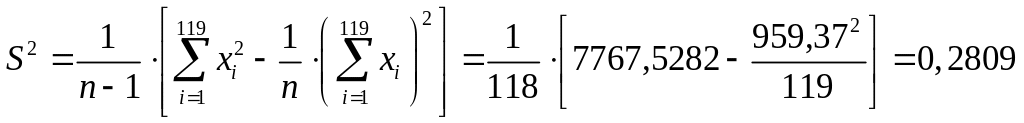и .

2. Сгруппируем данные табл. 6.1 по интервалам с шагом, вычисленным по соотношению

.

Начальная точка равна .

Найдем границы интервалов , включающих все данные табл. 6.1, а также подсчитаем, сколько значений величины Х попадает в каждый интервал, то есть найдем частоты n_i. Результаты запишем в табл. 6.2.

По данным табл. 6.2 построим гистограмму. Для этого отложим на оси х интервалы длиной и начертим гистограмму.

Табл. 6.2. Расчет высоты прямоугольников для построения гистограммы

I	Интервал xi	Число попаданий в i-ый интервал
0	7,03
1	7,27	3	0,0252	0,105
2	7,51	5	0,0420	0,175
3	7,75	13	0,1092	0,455
4	7,99	31	0,2605	1,085
5	8,23	29	0,2437	1,015
6	8,47	20	0,1681	0,700
7	8,71	11	0,0924	0,385
8	8,95	6	0,0504	0,210
9	9,19	1	0,0084	0,035

3. Предположим, что случайная величина распределена по нормальному закону распределения с параметрами и . Гипотезу о нормальном распределении случайной величины Х проверим по критерию согласия Пирсона.

Результаты вычислений занесем в табл. 6.3.

Д ля заполнения табл. 6.3 в столбец 2 занесем из табл. 6.2 концы интервалов x_i; затем заполняем столбец 3 по формуле . Далее находим значение функции Лапласа по данным табл. 7 приложения 3, используя линейное интерполирование. Считаем при x₀= – и x₁₀= +. Теоретическую вероятность находим по формуле (70) и записываем результаты между строк столбца 4. Затем вычисляем и выпишем из табл. 6.2.

Для расчета критерия Пирсона объединим первые и последние два интервала. Используя данные табл. 6.3, рассчитаем критерий согласия Пирсона 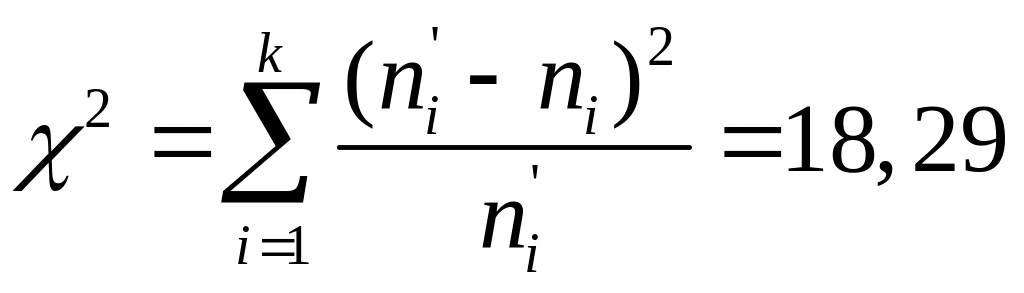. Число интервалов К=9. Число параметров, для которых были найдены оценки, r=2. Число степеней свободы f=К–r–1=9–2–1=6. В табл. 4 приложения 3 находим, что 16,9< <18,5. Следовательно, число 16,8 соответствует р=0,99, а число 18,5 соответствует р=0,995, то есть гипотеза о нормальном распределении не согласуется с истинным распределением с вероятностью 0,99–0,995 и мы имеем веские основания для принятия гипотезы о нормальном распределении случайной величины.

Табл. 6.3. Проверка гипотезы о нормальном распределении величины Х

i	xi			pi
0 1 2 3 4 5 6 7 8 9	7,03 7,27 7,51 7,75 7,99 8,23 8,47 8,71 8,95 9,19	- -1,4906 -1,0377 -0,5849 -0,1321 0,3208 0,7736 1,2264 1,6792 +	–0,5000 –0,4319 –0,3508 –0,2190 –0,0517 0,1255 0,2794 0,3907 0,4535 0,5000	0,0681 0,0811 0,1318 0,1673 0,1772 0,1539 0,1113 0,0628 0,0465	8,1039 9,6509 15,684 19,909 21,087 18,314 13,245 7,4732 5,5335	3 5 13 31 29 20 11 6 1

На гистограмме относительных частот (рис. 6.2) максимум сдвинут влево от середины интервала [7,0; 9,1], поэтому здесь вероятнее всего предложить наличие логарифмически нормального распределения или закона Вейбулла, чем нормального закона распределения.

Предположим сначала, что данное распределение подчинено закону Вейбулла и оценим сначала параметры  и  по формулам (67) и (68).

Найдем значение статистической функции F₉₇(x) для концов интервалов из табл. 6.2. Так, например, значение . Результаты остальных расчетов приведены в табл. 6.4.

Табл. 6.4. Проверка гипотезы о распределении величины Х по закону Вейбулла⁴

i	xi	F119(x)		pi
0 1 2 3 4 5 6 7 8 9	7,03 7,27 7,51 7,75 7,99 8,23 8,47 8,71 8,95 9,19	0,0252 0,0672 0,1765 0,4370 0,6807 0,8487 0,9412 0,9916 1,0000	0,9799 0,9485 0,8751 0,7211 0,4585 0,1632 0,0164 0,0001 2,55∙10-9 5,38∙10-19	0,0314 0,0734 0,154 0,2626 0,2953 0,1468 0,0163 0,0001 2,55∙10-9	3,7366 8,7346 18,326 31,2494 35,1407 17,4692 1,9397 0,0119 3∙10-7	3 5 13 31 29 20 11 6 1

С помощью табл. 6.4 решим уравнение F₁₁₉(t₁)=0,75 и F₁₁₉(t₂)=0,25. Число 0,75 находится между F₁₁₉(7,99) = 0,6807 и F₁₁₉(8,23)=0,8487.

Составим уравнение прямой, проходящей через точки с этими координатами: . Предположим, что точка с координатами (t₁; 0,75) лежит на этой прямой, то есть х=t₁, у=0,75. Тогда . Отсюда будем иметь .

Аналогично найдем t₂ из условия, что F₁₁₉(t₂)=0,25:

; ; .

Затем найдем оценки параметров и :

; .

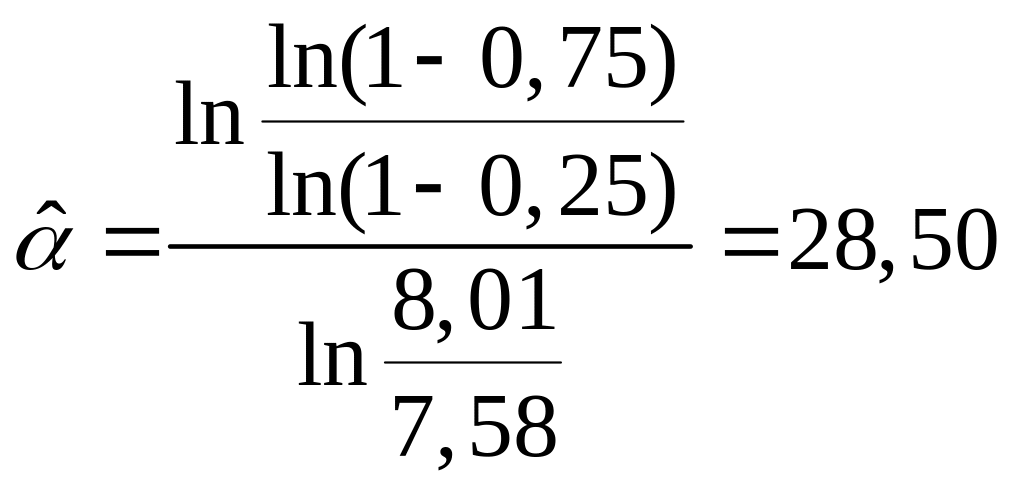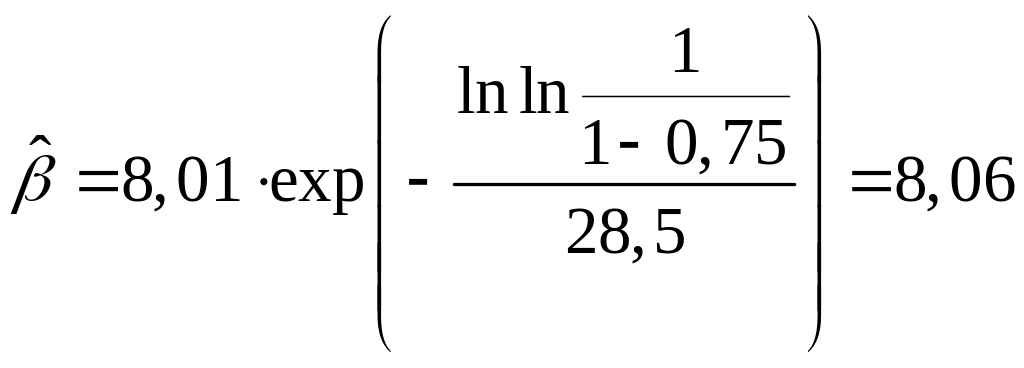Таким образом, предполагаемая функция плотности вероятности имеет вид

,

.

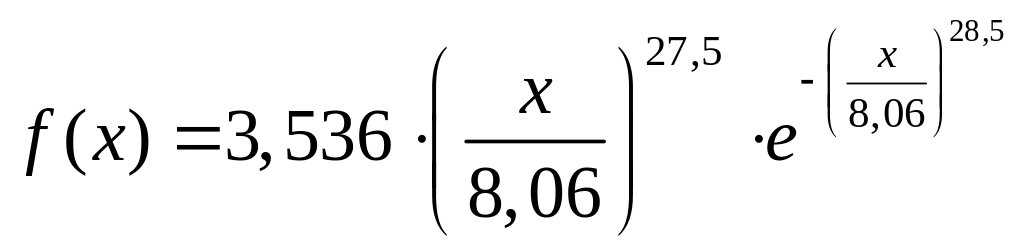Проверим, насколько это распределение Вейбулла согласуется с истинным распределением, используя критерий согласия Пирсона. Для расчета критерия Пирсона объединим первый и второй интервалы и шестой, седьмой, восьмой и девятый интервалы. Результаты вычислений заносим в табл. 6.4: . В табл. 4 приложения 3 находим, что >10,6 (при f=К–r–1=5–2–1=4). Следовательно, число 10,6 соответствует р=0,995, то есть гипотеза о распределении Вейбулла не согласуется с истинным распределением с вероятностью p>0,995 и мы имеем веские основания для отвержения гипотезы о распределении случайной величины по закону Вейбулла.

Выдвинем гипотезу о логарифмически нормальном распределении. Оценим параметры этого распределения по формулам

; ; .

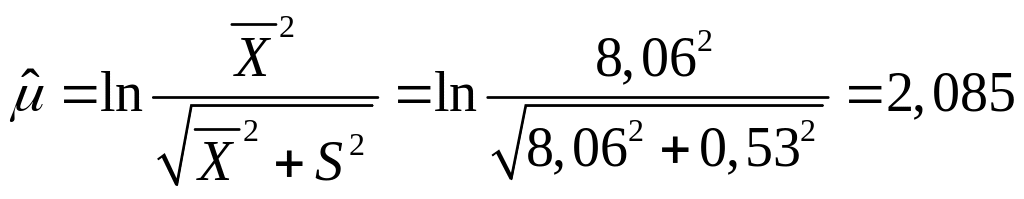Тогда предполагаемая функция вероятностей имеет вид

; .

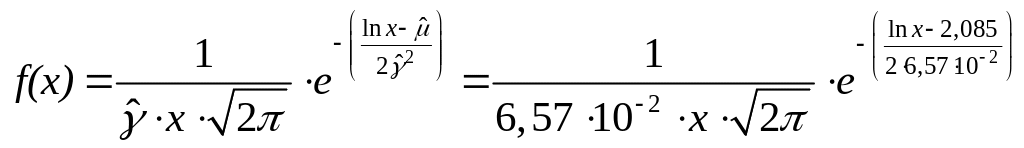Сделаем проверку гипотезы о логарифмически нормальном распределении по критерию согласия Пирсона (табл. 4 приложения 3).

Как можно видеть, значение критерия велико, следовательно, логарифмически нормальное распределение отклоняется.

Табл. 6.5. Проверка гипотезы о логарифмически нормальном распределении величины Х

i	xi			pi
0 1 2 3 4 5 6 7 8 9	7,03 7,27 7,51 7,75 7,99 8,23 8,47 8,71 8,95 9,19	– –0,7705 –0,5233 –0,2839 –0,0518 0,1734 0,3922 0,6048 0,8117 +	–0,5000 –0,2794 –0,1985 –0,1103 –0,0199 0,0675 0,1517 0,2257 0,2910 0,5000	0,2206 0,0809 0,0882 0,0904 0,0874 0,0842 0,074 0,653 0,209	26,2514 9,6271 10,4958 10,7576 10,4006 10,0198 8,806 77,707 24,871	3 5 13 31 29 20 11 6 1

Исходя из приведенного расчета видно, что наиболее удачно приведенное распределение описывает нормальное распределение величины Х, т.е. нормальное распределении имеет функцию плотности вероятности:

Таким образом, окончательное уравнение имеет вид

.

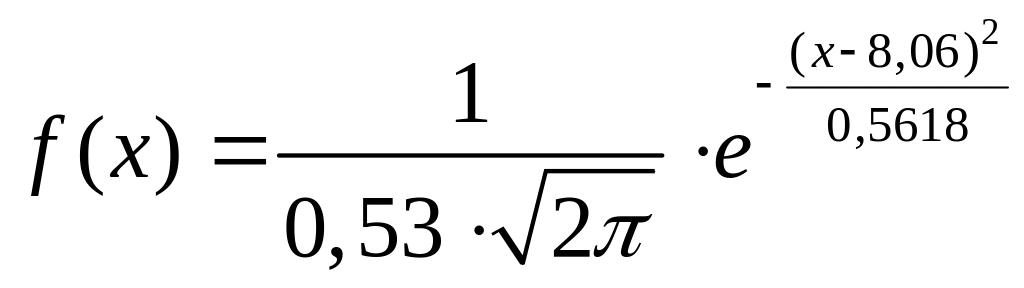4. Поскольку распределение величины Х не является нормальным, но число опытов достаточно велико (n=119>30), мы воспользуемся приближенными формулами:

и

При подборе распределения величины Х значение р[0,99; 0,995]. Исходя из этого, принимаем, что величина q=0,005. По табл. 7 приложения 3 значение аргумента соответствует значению функции , тогда . Тогда

и

и с вероятностью 0,99 имеем , а также .

Вывод:

Массив экспериментальных данных подчиняется нормальному закону распределения (является однородным). Исходя из этого его можно использовать для стандартной обработки данных.

1 Пусть некоторая функция у=у(х) представляет из себя таблицу, где x_i – значение аргумента, y_i – соответствующее значение функции. Требуется найти значение функции для аргумента х₁<х<х₂ по данным значения у₁<у<у₂ или наоборот по данному у найти х. Предположим, что на участке (х₁, х₂) график функции имеет линейную зависимость, тогда уравнение прямой будет иметь вид . Поскольку отрезок [х₁, х₂] мал, то в точке х ордината у(х) мало отличается от ординаты прямой. Из уравнения прямой находим неизвестное х или у. Такой метод называется линейное интерполирование.

2 Заметим, что значение .

3 В качестве действительного значения принимают среднеарифметическое значение результата измерений.

4 Заметим, что значение .

108