6. Примеры выполнения практических заданий Примеры решения типовых задач

Пример 1. При проведении измерительного эксперимента получены следующие значения величины: 11,65; 11,41; 11,57; 11,60; 11,50; 11,55; 11,58; 11,58; 11,61; 11,63. Требуется проанализировать полученные результаты наблюдений в целях выявления грубых погрешностей, используя критерий Диксона.

Решение:

1. Располагаем результаты наблюдений в вариационный возрастающий ряд:

11,41<11,50<11,55<11,57<11,58;11,58<11,60<11,61<11,63<11,65.

2. Записываем используемую для расчета формулу критерия Диксона:

.

3. Подставляем в формулу данные нашего эксперимента и рассчитываем К_д:

.

4. Зададимся значением q=0,10 (десятипроцентным уровнем значимости).

5. Используя табличные данные, выявим критическую область для рассчитанного критерия К_д.

Согласно таблице 2 приложения 3 при n=10 и q=0,15, z_дикс =0,35.

6. Делаем вывод, что К_д < z_дикс.

Ответ. Полученный ряд результатов наблюдений не имеет в своем составе грубых погрешностей даже при q=0,1. Дальнейшей обработке будет подвергаться весь массив данных.

Пример 2. В процессе контроля были получены следующие результаты измерительных наблюдений за одним из показателей качества: 9,47; 9,49; 9,40; 9,61; 9,39; 9,41; 9,43; 9,49; 9,46; 9,42. Используя критерий Романовского выявить наличие промахов.

Решение:

1. Располагаем результаты в вариационный возрастающий ряд: 9,39<9,40<9,41<9,42<9,43<9,46<9,47<9,49<9,49<9,61.

2. Выявляем результат, вызывающий сомнение:

Результат 9,61 вызывает сомнение, так как резко отличается от всех остальных (х_i=9,61).

3. Запишем основную расчетную формулу:

.

При расчете результат х_i=9,61 все принимаем во внимание.

4. Вычисляем среднее арифметическое без учета сомнительного варианта

;

n=10-1=9

=9,39+9,40+9,41+9,42+9,43+9,46+9,47+9,49+9,49=84,96

5. Находим среднеквадратическое отклонение среднего арифметического результата наблюдения по формуле

;

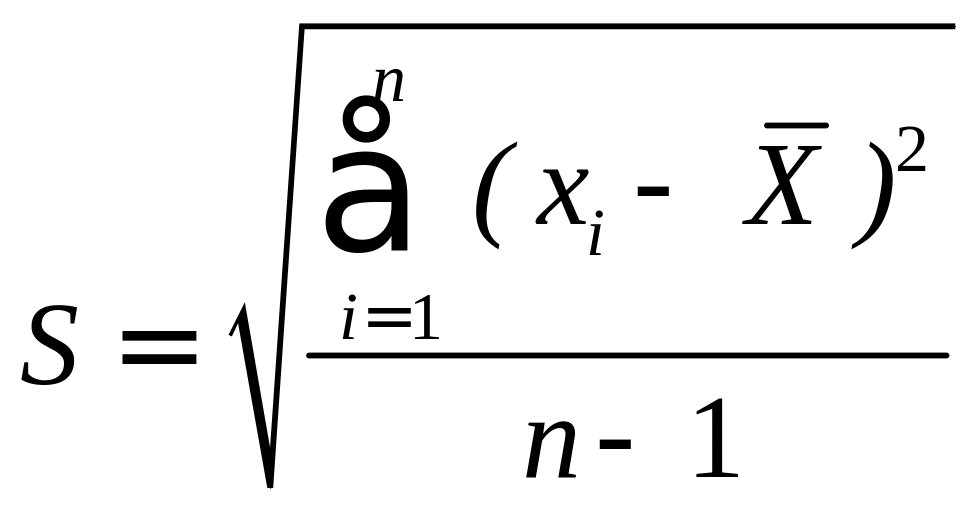Разность хi –	Квадрат разности
х1- =9,39-9,44=-0,05	0,0025	0,0118
х2- =9,40-9,44=-0,04	0,0016
х3- =9,41-9,44=-0,03	0,0009
х4- =9,42-9,44=-0,02	0,0004
х5- =9,43-9,44=-0,01	0,0001
х6- =9,46-9,44=0,02	0,0004
х7- =9,47-9,44=0,03	0,0009
х8- =9,49-9,44=0,05	0,0025
х9- =9,49-9,44=0,05	0,0025

Определяем число степеней свободы f=n-1=9-1=8

Рассчитываем стандартное отклонение:

;

6. Подставляем полученные расчетные данные в основную формулу (14):

.

7. Находим табличное значение критерия Романовского для n =10 и принятого уровня значимости q=0,1: =2,29.

8. Вывод: рассчитанное значение .

Ответ: Так как сомнительный результат наблюдения равный 9,61 является грубой погрешностью и в дальнейшей обработке полученных данных не используется.

Пример 3. Некоторую физическую величину измерили двумя независимыми способами. По первому способу получили результаты:38.20,38.00,37.66; по второму – 37.70,37.65,37.55. Значимо ли различаются результаты данных измерений?

Решение:

1. По формуле (6) рассчитаем среднее арифметическое значение для каждого способа:

и

2. Рассчитаем дисперсии по формуле (8):

3. Проведем сравнение точности обоих методов, используя F-распределение:

F_эксп =

Полученные значения F_эксп, сопоставляем с табличным (таблица 6, приложения 3) значением F распределения при р=0.95 и числах степеней свободы f ₁ =2 и f ₂ =2.

Так как F _табл= 19.00> F _эксп=12.78, то расхождение между дисперсиями незначимо и, следовательно, способ измерения физической величины одинаковой точности.

С помощью t-критерия оцениваем расхождение между . Среднее взвешенное двух дисперсий и t-критерий рассчитываем по формулам

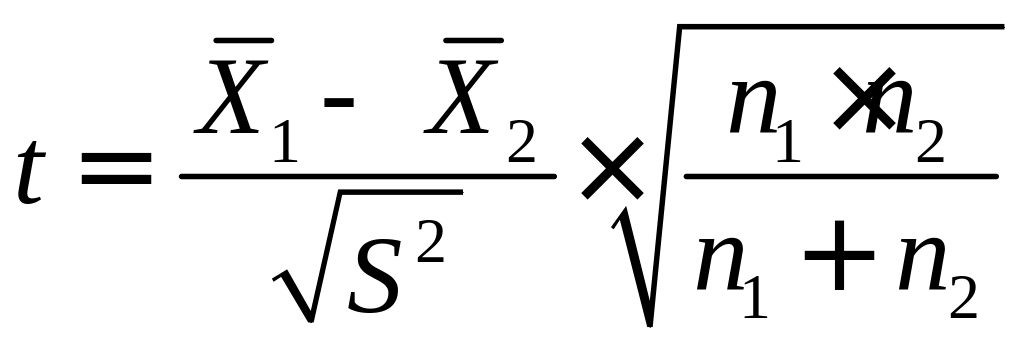и , тогда

t _эксп =

Сопоставляем полученное значение t _эксп с табличными t _0.95;4 = 2,776 (при р= 0,95 и f = 3+3-2=4). Так как t _эксп =1.96 < t _0.95;4 = 2,776, то различие между незначимо. Следовательно, все результаты обоих измерений отражают истинное значение физической величины.

Поэтому данные измерения могут быть представлены в виде

;

где – среднее арифметическое из всех n₁+n₂ результатов:

4. Вычисляем среднее значение измерений (среднее арифметическое) по формуле (1):

=

Определим среднее квадратическое отклонение S по формуле (9):

S =

Рассчитаем доверительные границы действительного значения результата измерения, исходя из данных наблюдений, полученных обоими способами, по формуле (15). Для расчета необходимое значение t_0,95;5 находим по таблице (см. приложение 3, табл. 1)

Ответ. Результат измерений физической величины, рассчитанный по данным наблюдений полученных двумя способами, записываем следующим образом: 37.79 6

Пример 4. При измерении некоторой величины были получены следующие результаты: 1.31, 1.45,1.42,1.32, 1.30. Опорное значение этой величины Х_оп = 1,47.

Определить стандартное отклонение S, точность измерений _0.95 ( ,%) и сделать вывод о наличии систематической ошибки в использовании данного метода измерения.

Решение:

1. По формуле (6) вычисляем среднее значение измерений (среднее арифметическое):

=

2.По формуле (9) вычисляем стандартное отклонениеS:

S = ;

3. По формуле (15) рассчитываем доверительные границы случайной составляющей погрешности результата измерения. Значение коэффициента Стьюдента находим из таблицы (см. приложение 3, табл.1).

4. Покажем доверительный интервал действительного значения величины:

;

5. Точность метода обычно выражают в форме относительной погрешности, которая рассчитывается по формуле (22)

Ответ. Данный метод измерения НКПРП имеет систематическую погрешность, так как опорное значение Х_оп = 1,47 не попадает в доверительный интервал 1,27 1,45. Точность измерения является очень низкой для данного метода.

Пример 5. Определить, существует ли значимое различие между выборочной средней величиной при определении НКПРП пыли обращающейся в производстве, если при отборе проб следующие результаты: 2.10, 2.12, 2.13, 2.15, 2.15 и средней генеральной совокупностью (для n=80) =2.15 г/м³.

Решение:

1.Среднее арифметическое значение вычисляем по формуле (6):

2.Стандартное отклонение отдельного определения вычисляем по формуле (9):

,

3.Из формулы (15) находим значение величины t:

Из таблицы значений коэффициента Стьюдента (смотри таблицу 1 приложения 3) для f=4 и p=0,95, t_р,f=2,78, что больше рассчитанного из формулы (15) 2,11.

Ответ. Следовательно, средняя величина не отличается значимо от средней  генеральной совокупности.

Пример 6. При определении коэффициента теплопроводности газобетона были получены результаты: 8.010^–4 Вт/м^оС и 8.410^–4 Вт/м^оС. Чему равна точность изменения (_р и ) коэффициента теплопроводности? Сколько параллельных измерений необходимо провести для достижения относительной точности 5%? Оправдано ли будет применение этого способа измерения для достижения такой точности?

Решение:

1. По формуле (6) находим среднее арифметическое значение:

2.Стандартное отклонение единичного результата вычисляем по формуле (9):

,

По таблице 1 приложения 3 находим для р=0.95 и f=2-1=1 t_р,f=12.7 и по формуле (15) вычисляем точность метода:

3. Определяем относительную точность измерения по формуле (22):

Если необходимо получить =5%, то

или

Из формулы (15)

Если принять n=4, то t=2.90. Исходя из данных таблице 1 (см. приложение 3) для р=0.95 и f=4–1=3 t_р,f=3.18, что не обеспечивает точности 5%. Если принять n=5, то t=3.24. По таблице 1 (см. приложение 3) для р=0.95 и f=5–1=4 t_р,f=2.78, что меньше рассчитанного t=3.24. Следовательно, при n=5 величина t=3.24 дает большую вероятность, чем 0.95.

Ответ. Для достижения относительной погрешности 5% необходимо провести 5 измерений. Так как n<8 (n=5), то можно считать, что данный метод вполне оправдан для достижения точности 5%.

Пример 7

Пример построения гистограммы и проверка гипотезы о распределении случайной величины

Даны 98 независимых равноточных измерений некоторой физической величины:

120.13 120.76 119.39 118.88 121.11 121.66 119.58

118.49 119.00 119.18 120.90 120.53 121.92 119.76

121.19 121.35 120.16 119.31 121.25 119.96 120.84

117.17 120.82 119.59 120.57 119.67 119.92 120.51

121.76 121.31 119.61 119.62 120.59 119.00 119.85

119.95 119.43 121.07 121.84 122.21 120.20 119.56

119.37 119.34 120.89 120.06 119.95 121.47 119.65

119.90 119.75 120.50 119.99 119.54 120.87 120.25

119.55 119.01 120.03 120.71 120.10 118.73 120.90

120.31 119.83 121.46 122.21 118.40 119.36 120.86

119.72 119.22 119.91 120.62 120.63 119.56 120.07

121.68 120.80 120.16 119.92 121.03 120.17 119.43

119.85 120.52 120.45 119.57 121.11 120.06 120.02

121.64 119.91 119.42 119.31 121.39 120.06 119.55

Рассчитать:

1. При уровне значимости 0.05 исследовать предложенную выборку на однородность. Исключить все грубые ошибки с вероятностью 1–q. Найти среднее значение и эмпирический стандарт S полученной однородной выборки.

2. Сгруппировать однородную выборку по интервалам, построить гистограмму относительных частот, сформировать гипотезу о виде распределения случайной величины Х.

3. Проверить гистограмму о распределении величины Х по критерию согласия Пирсона, установить вероятность р, с которой высказанная гипотеза не согласуется с истинным распределением. Если р<0.50, то данную гипотезу не отвергать, остановиться на данном виде распределения и перейти к пункту 4. Если р>0.50, то выбрать другой закон распределения и снова применить к нему критерий согласия Пирсона. Если при исследовании гипотез о трех различных распределениях (нормальном, логарифмическом и распределении Вейбулла) вероятность несогласования р>0.50, то выбрать лучшее по вероятности распределения.

4. Найти доверительный интервал для математического ожидания M(X)=m и среднего квадратичного отклонения (X)=, если задан уровень значимости q, полученной в пункте 3 при выборе распределения величины Х.

Решение:

1. Исследуем данную выборку на однородность. Для этого все результаты измерений расположим в порядке возрастания. Результат запишем в виде табл. 1.

По условию требуется проверить, не содержит ли данная выборка грубых ошибок на уровне значимости 0.05, то есть из выборки следует исключить те х_i, которые с вероятностью 1–q=0.95.

Найдем критическое значение числа

,

с которым будем сравнивать максимальное отклонение t(x_i). Нанесем на ось все значения из табл. 6.1.

Табл. 6.1. Экспериментальные значения величины Х

I	xi	i	xi	i	xi	i	xi
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25	117.17 118.40 118.49 118.73 118.88 119.00 119.00 119.01 119.18 119.22 119.31 119.34 119.35 119.36 119.37 119.37 119.39 119.42 119.43 119.43 119.54 119.55 119.55 119.56 119.56	26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50	119.57 119.58 119.59 119.61 119.62 119.65 119.72 119.75 119.76 119.83 119.85 119.85 119.90 119.91 119.91 119.92 119.92 119.95 119.95 119.96 119.99 120.02 120.03 120.06 120.06	51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75	120.06 120.07 120.10 120.13 120.16 120.16 120.17 120.20 120.25 120.31 120.45 120.50 120.51 120.52 120.53 120.57 120.59 120.62 120.63 120.71 120.76 120.80 120.82 120.84 120.86	76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98	120.87 120.89 120.90 120.90 121.03 121.07 121.11 121.11 121.19 121.25 121.31 121.35 121.39 121.46 121.47 121.64 121.66 121.68 121.76 121.84 121.92 122.21 122.21

Рис. 6.1. Распределение случайной величины

Как можно видеть из рис. 6.1, наиболее густо точки расположены в интервале [119, 122]. Значение x₁=117.17 резко отличается от интервала [119, 122], что может служить косвенным подтверждением того, что величина x₁ является грубой ошибкой. Остальные значения x_i не вызывают особых подозрений, поэтому мы исследуем дополнительно крайние точки x₁, x₂, x₉₇ и x₉₈.

Временно отбросив указанные значения, подсчитаем среднее арифметическое значение и эмпирический стандарт:

;

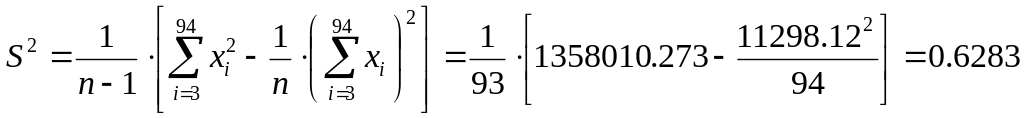и .

Исследуем сначала x₁=117.17, применив к нему наш критерий. Оказалось, что . Исходя из приведенного расчета видно, что значение . Следовательно, x₁=117.17 является грубой ошибкой, и поэтому данное значение должно быть исключено из результатов обработки.

Применим t-критерий к значению x₂=118.40. Расчет значения t-критерия дает следующую величину . Так как , то включив в выборку x₂=118.40, пересчитаем с учетом его и .

Получим

;

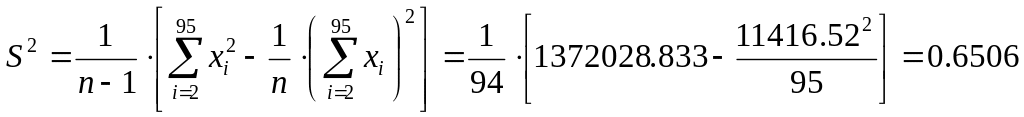и .

Вычислим . Таким образом, значения x₉₇=x₉₈=121.21 также принадлежат к выборке, поэтому включаем их в выборку и с вероятностью 1–р=0.95 выборка, представленная в табл. 6.1, является однородной.

Для полученной выборки находим

;

и .

2. Сгруппируем данные табл. 6.1 по интервалам с шагом, вычисленным по соотношению

.

Начальная точка равна .

Найдем границы интервалов , включающих все данные табл. 6.1, а также подсчитаем, сколько значений величины Х попадает в каждый интервал, то есть найдем частоты n_i. Результаты запишем в табл. 6.2.

По данным табл. 6.2 построим гистограмму. Для этого отложим на оси х интервалы длиной и начертим гистограмму.

Табл. 6.2. Расчет высоты прямоугольников для построения гистограммы

I	Интервал xi	Число попаданий в i-ый интервал
0 1 2 3 4 5 6 7 8 9 10 11	118.215 118.585 118.955 119.325 119.695 120.065 120.435 120.805 121.175 121.545 121.915 122.285	2 2 6 20 20 9 12 11 7 5 3	0.0206 0.0206 0.0619 0.2062 0.2062 0.0928 0.1237 0.1134 0.0722 0.0515 0.0309	0.0557 0.0557 0.1673 0.5573 0.5573 0.2508 0.3343 0.3065 0.1951 0.1392 0.0835

3. Предположим, что случайная величина распределена по нормальному закону распределения с параметрами и . Гипотезу о нормальном распределении случайной величины Х проверим по критерию согласия Пирсона.

Результаты вычислений занесем в табл. 6.3.

Для заполнения табл. 6.3 в столбец 2 занесем из табл. 6.2 концы интервалов x_i; затем заполняем столбец 3 по формуле . Далее находим значение функции Лапласа по данным табл. 7 приложения 3, используя линейное интерполирование. Считаем при x₀= – и x₁₀= +. Теоретическую вероятность находим по формуле (70) и записываем результаты между строк столбца 4. Затем вычисляем и в ыпишем из табл. 6.2.

Для расчета критерия Пирсона объединим первые и последние два интервала. Используя данные табл. 6.3, рассчитаем критерий согласия Пирсона . Число интервалов К=9. Число параметров, для которых были найдены оценки, r=2. Число степеней свободы f=К–r–1=9–2–1=6. В табл. 4 приложения 3 находим, что 12.6< <14.4. Следовательно, число 12.6 соответствует р=0.95, а число 14.4 соответствует р=0.975, то есть гипотеза о нормальном распределении не согласуется с истинным распределением с вероятностью 0.95–0.975 и мы имеем веские основания для принятия гипотезы о нормальном распределении случайной величины.

Табл. 6.3. Проверка гипотезы о нормальном распределении величины Х

i	xi			pi
0 1 2 3 4 5 6 7 8 9 10 11	118.215 118.585 118.955 119.325 119.695 120.065 120.435 120.805 121.175 121.545 121.915 122.285	– –1.9247 –1.4891 –1.0536 –0.6180 –0.1825 0.2531 0.6886 1.1242 1.5597 1.9953 +	–0.5000 –0.4729 –0.4320 –0.3545 –0.2317 –0.0724 0.0999 0.2318 0.3857 0.4404 0.4764 0.5000	0.0271 0.0409 0.0775 0.1228 0.1593 0.1723 0.1319 0.1539 0.0547 0.0360 0.0236	2.6287 3.9673 7.5175 11.9116 15.4521 16.7131 12.7943 14.9283 5.3059 3.4920 2.2892	2 2 6 20 20 9 12 11 7 5 3

На гистограмме относительных частот (рис. 6.2) максимум сдвинут влево от середины интервала [118.4, 122.2], поэтому здесь вероятнее всего предложить наличие логарифмически нормального распределения или закона Вейбулла, чем нормального закона распределения.

Предположим сначала, что данное распределение подчинено закону Вейбулла и оценим сначала параметры  и  по формулам (67) и (68).

Найдем значение статистической функции F₉₇(x) для концов интервалов из табл. 6.2. Так, например, значение . Результаты остальных расчетов приведены в табл. 6.4.

Табл. 6.4. Проверка гипотезы о распределении величины Х по закону Вейбулла²

i	xi	F97(x)		pi
0 1 2 3 4 5 6 7 8 9 10 11	118.215 118.585 118.955 119.325 119.695 120.065 120.435 120.805 121.175 121.545 121.915 122.285	0.0206 0.0412 0.1031 0.3093 0.5155 0.6082 0.7320 0.8454 0.9175 0.9691 1.0000	0.9208 0.8771 0.8120 0.7189 0.5931 0.4379 0.2716 0.1281 0.0394 0.0062 0.0003 3.69·10–6	0.0437 0.0651 0.0931 0.1258 0.1552 0.1663 0.1435 0.0887 0.0332 0.0059 0.0003	4.2389 6.3147 9.0307 12.2026 15.0932 16.1311 13.9195 8.6039 3.2204 0.5723 0.0291	2 2 6 20 20 9 12 11 7 5 3

С помощью табл. 6.4 решим уравнение F₉₇(t₁)=0.75 и F₉₇(t₂)=0.25. Число 0.75 находится между F₉₇(120.435)=0.7320 и F₉₇(120.805)=0.8454.

Составим уравнение прямой, проходящей через точки с этими координатами: . Предположим, что точка с координатами (t₁; 0.75) лежит на этой прямой, то есть х=t₁, у=0.75. Тогда . Отсюда будем иметь .

Аналогично найдем t₂ из условия, что F₉₇(t₂)=0.25:

; ; .

Затем найдем оценки параметров и :

; .

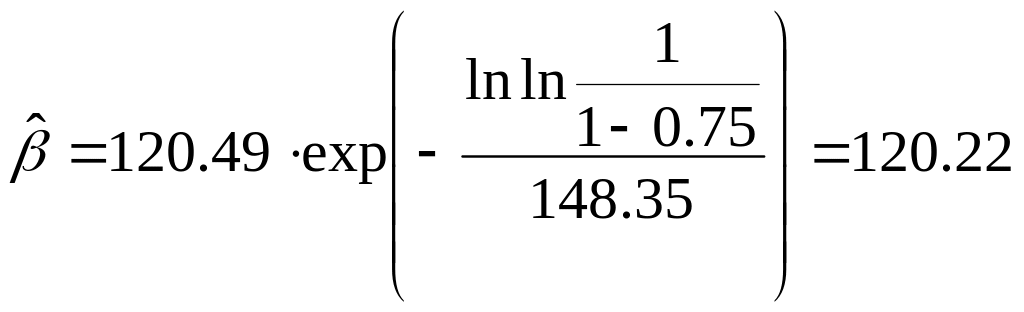Таким образом, предполагаемая функция плотности вероятности имеет вид

,

.

Проверим, насколько это распределение Вейбулла согласуется с истинным распределением, используя критерий согласия Пирсона. Для расчета критерия Пирсона объединим первый и второй интервалы и восьмой–одиннадцатый интервалы. Результаты вычислений заносим в табл. 6.4: . В табл. 4 приложения 3 находим, что >14.9 (при f=К–r–1=7–2–1=4). Следовательно, число 14.9 соответствует р=0.995, то есть гипотеза о распределении Вейбулла не согласуется с истинным распределением с вероятностью p>0.995 и мы имеем веские основания для отвержения гипотезы о распределении случайной величины по закону Вейбулла.

Выдвинем гипотезу о логарифмически нормальном распределении. Оценим параметры этого распределения по формулам (58) и (59). Находим, что

; ; .

Тогда предполагаемая функция вероятностей имеет вид

; .

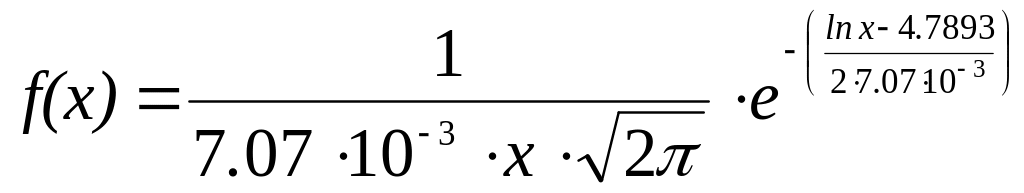Сделаем проверку гипотезы о логарифмически нормальном распределении по критерию согласия Пирсона (табл. 4 приложения 3).

Как можно видеть, значение критерия велико, следовательно, логарифмически нормальное распределение отклоняется.

Табл. 6.5. Проверка гипотезы о логарифмически нормальном распределении величины Х

i	xi			pi
0 1 2 3 4 5 6 7 8 9 10 11	118.215 118.585 118.955 119.325 119.695 120.065 120.435 120.805 121.175 121.545 121.915 122.285	– –0.9674 –0.7467 –0.5272 –0.3081 –0.0896 0.1281 0.3452 0.5616 0.7774 0.9925 +	–0.5000 –0.3336 –0.2721 –0.2009 –0.1209 –0.0357 0.0510 0.1350 0.2128 0.2815 0.3395 0.5000	0.1664 0.0615 0.0712 0.0800 0.0852 0.0867 0.0840 0.0778 0.0687 0.0580 0.1605	16.1408 5.9655 6.9064 7.7600 8.2644 8.4099 8.1480 7.5466 6.6639 5.6260 15.5685	2 2 6 20 20 9 12 11 7 5 3

Исходя из приведенного расчета видно, что наиболее удачно приведенное распределение описывает нормальное распределение величины Х. Таким образом, окончательное уравнение имеет вид

.

4. Поскольку распределение величины Х не является нормальным, но число опытов достаточно велико (n=97>30), мы воспользуемся приближенными формулами (73) и (74).

При подборе распределения величины Х значение р[0.95, 0.975]. Исходя из этого, принимаем, что величина q=0.05. По табл. 7 приложения 3 значение аргумента соответствует значению функции , тогда . Тогда

и

и с вероятностью 0.95 имеем , а также .

Пример 8

С помощью тестера (мультиметра), работающего в режиме измерения переменного напряжения, получено значение U_изм=120 В. Диапазон измерений прибора от 0 до 50 В. В паспорте указано, что при работе в этом диапазоне относительная погрешность не превышает двух процентов. Записать результат измерения.

Решение:

1. Результат измерения обычно записывается в форме: Х_д=Х_изм+ Х; для нашего случая эта запись будет иметь вид

U_д= U_изм+ U, при относительной погрешности ,

где U_изм – измеренное значение (120 В); U – абсолютная погрешность измерения; - относительная погрешность (2%).

2. Абсолютная погрешность определяется из формулы:

, откуда U= /100%

U=2%*120 В/100%=2,4 В.

Ответ: Результат измерения записывается в виде U = (120,0 2,4 В) при = 2 %. Запись 120,0 применяется, исходя из записи погрешности, имеющей знак после запятой (2,4). Поэтому при записи результата измерения это учитывается.

Пример 9

Для выполнения измерений применялось средство измерения с классом точности 2,5, со шкалой, проградуированной от 0 до 5 и ценой деления 0,2. Было получено значение величины A=3. Записать результат измерения.

Решение:

1. Результат измерения записывается обычно в форме

А_д=А_изм А при относительной погрешности ,%,

где А_изм – измеренное значение величины, А – абсолютная погрешность, относительная погрешность.

Для решения задачи вспомним обозначение погрешностей через класс точности измерительного прибора.

2. Если класс точности обозначим 2,5, это означает, что приведенная погрешность _н = 2,5%.

Воспользуемся формулой приведенной погрешности:

,

где А_н – ширина диапазона измерений.

Из этой формулы следует, что

, тогда

.

Относительная погрешность измерения рассчитывается по формуле:

.

.

Ответ: Результат измерения запишем А_д=(3,000 0,125) при относительной погрешности .

Число знаков после запятой в записи результата и погрешности должно быть одинаково.

Пример 10

Для выполнения измерений применялось средство измерения с классом точности , со шкалой, проградуированной от 0 до 10 и ценой деления 0,2. Было получено значение величины A=4. Записать результат измерения.

Решение:

Решение задачи осуществляется аналогично примеру 9.

1. Если класс точности обозначается , это значит, что относительная погрешность =5,0%. Тогда

Ответ: Результат измерения запишется как А=4,0 0,5 при =5,0%.

Пример 11

Для выполнения измерений применялось средство измерения с классом точности 2,5/1,0, со шкалой, проградуированной от 0 до 10 и ценой деления 0,2. Было получено значение величины A=6. Записать результат измерения.

Решение:

1. Если класс точности обозначается 2,5/1,0, это значит, что указаны приведенные погрешности в конце и в начале диапазона измерений соответственно: =2,5%, =1,0%.

Для расчета относительной погрешности результата измерения используется формула

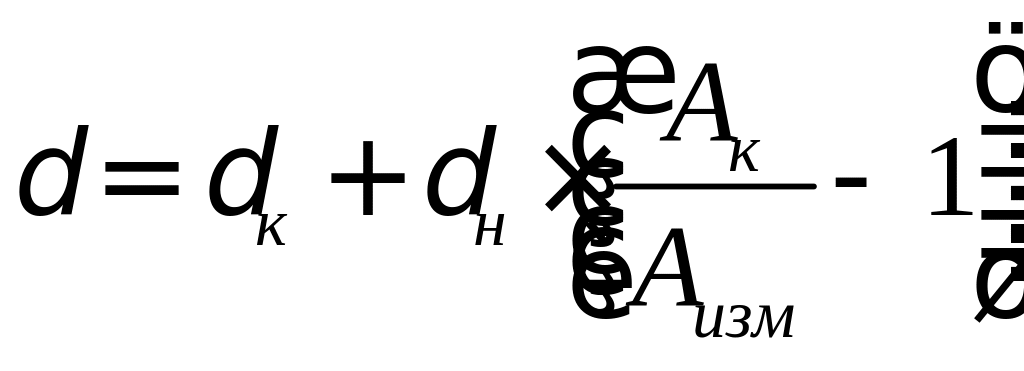,%, т.е.

%.

2. Рассчитываем абсолютную погрешность измерения

,

(единицы измерения)

Ответ: Результат измерения запишется как А=6,00 0,19 при =3,17%.

Примечание.

Если будем иметь данное не об одном, а о нескольких результатах наблюдения одной и той же величины, полученных с использованием одного и того же средства измерения, то следует с начала определить среднее арифметическое значение, которое и будет приниматься за измеренное значение.

Пример 12

Необходимо определить степень согласованности мнения пяти экспертов. Результаты мнения экспертов представлены следующим образом.

№1	-	Q1	Q2	Q3	Q4	Q5	Q6	Q7
№2	-	Q3	Q1	Q2	Q5	Q6	Q7	Q4
№3	-	Q1	Q2	Q5	Q3	Q6	Q4	Q7
№4	-	Q1	Q3	Q2	Q5	Q4	Q6	Q7
№5	-	Q3	Q1	Q5	Q2	Q6	Q4	Q7

Решение:

Для решения используем формулу:

,

W – коэффициент конкордации;

S – сумма квадратов отклонений всех оценок рангов каждого объекта экспертизы от среднего значения;

n – число экспертов;

m – число объектов экспертизы.

0<W<1

При W=0 – полная несогласованность

W=1 – полное единодушие.

Лучше все расчетные данные свести в таблицу

№ объекта экспертизы	Оценка эксперта					сумма рангов	Qср.	Отклонение от среднего	Квадрат отклонения	Сумма квадратов отклонений (S)	12S	n2	m3	m3-m	W
	1	2	3	4	5
1	1	2	1	1	2	7	20	13	169	596	7152	25	343	336	0,85
2	2	3	2	3	4	14		6	36
3	3	1	4	2	1	11		9	81
4	4	7	6	5	6	28		-8	64
5	5	4	3	4	3	19		1	1
6	6	5	5	6	5	27		-7	49

.

Ответ: Мнения экспертов достаточно согласованы.

Пример 13

Необходимо определить степень согласованности мнения девяти экспертов.

Результаты мнения экспертов представлены следующим образом.

№1	-	Q3	Q2	Q1	Q5	Q6	Q4
№2	-	Q2	Q3	Q1	Q5	Q4	Q6
№3	-	Q3	Q1	Q2	Q6	Q4	Q5
№4	-	Q4	Q2	Q3	Q1	Q6	Q5
№5	-	Q3	Q1	Q4	Q2	Q5	Q6
№6	-	Q1	Q2	Q5	Q3	Q6	Q4
№7	-	Q3	Q2	Q5	Q1	Q4	Q6
№8	-	Q1	Q3	Q2	Q5	Q4	Q6
№9	-	Q3	Q1	Q4	Q2	Q6	Q5

Решение:

Для решения используем формулу:

,

W – коэффициент конкордации;

S – сумма квадратов отклонений всех оценок рангов каждого объекта экспертизы от среднего значения;

n – число экспертов;

m – число объектов экспертизы.

0<W<1

При W=0 – полная несогласованность

W=1 – полное единодушие.

Лучше все расчетные данные свести в таблицу

№ объекта экспертизы	Оценка эксперта									сумма рангов	Qср.	Отклонение от среднего	Квадрат отклонения	Сумма квадратов отклонений (S)	12S	n2	m3	m3-m	W
	1	2	3	4	5	6	7	8	9
1	3	3	2	4	2	1	4	1	2	22	31,5	9,5	90,25	821,5	9858	81	216	210	0,57
2	2	1	3	2	4	2	2	3	4	23		8,5	72,25
3	1	2	1	3	1	4	1	2	1	16		15,5	240,25
4	6	5	5	1	3	6	5	5	3	39		-7,5	56,25
5	4	4	6	6	5	3	3	4	6	41		-9,5	90,25
6	5	6	4	5	6	5	6	6	5	48		-16,5	272,25

.

Ответ: Мнения экспертов разделились, поэтому необходимо применить или другой метод или поставить вопрос об изменении состава экспертной комиссии.

Пример выполнения практического задания №36

Дать характеристику НПБ 305-2001. Пожарная техника. Заряды к воздушно-пенным огнетушителям и установкам пенного пожаротушения. Общетехнические требования. Методы испытаний.

1. НПБ 305-2001. Пожарная техника. Заряды к воздушно-пенным огнетушителям и установкам пенного пожаротушения. Общетехнические требования. Методы испытаний.

2. Норма. Норма является одним из видов нормативных документов (НД), действующих на территории РФ. НПБ 305-2001. Пожарная техника. Заряды к воздушно-пенным огнетушителям и установкам пенного пожаротушения. Общетехнические требования. Методы испытаний. Представляет собой НД, устанавливающий количественные критерии к объектам и носит методический характер.

3. НПБ 305-2001 внесены на разработку отделом техники и вооружения ГУ ГПС МЧС России.

4. НПБ 305-2001 разработаны ФГУ ВНИИПО МВД России.

5. НПБ 305-2001 утверждены приказом ГУ ГПС МВД России от –3-10.2001 г. № 68.

6. Объектом стандартизации являются заряды к воздушно-пенным огнетушителям и установкам пенного пожаротушения.

7. НПБ 305-2001 применяется в области пожарной безопасности и устанавливает критерии по основным показателям качества зарядов к воздушно-пенным огнетушителям и установкам пенного пожаротушения, а также дает описание общих технических требований к ним и методов их испытаний. НПБ 305-2001 предназначены для пожарных специалистов, а также организаций, проводящих различного рода проверки и контроль в соответствие с заданными целями.

8. НПБ 305-2001 применяются в области пожарной безопасности и устанавливают требования к зарядам для воздушно-пенных огнетушителей и установок пенного пожаротушения, предназначенным для тушения пожаров классов А и В.

9. Структура НПБ 305-2001 устанавливает положения ГОСТ Р1.5.92. ГСС РФ. Общие требования к построению, изложению, оформлению и содержанию стандартов». Рассматриваемый документ построен в следующем порядке:

• область применения;

• термины и определения;

• классификация;

• общие технические требования;

• требования безопасности;

• правила приемки;

• методы испытаний;

• маркировка и упаковка;

• нормативные ссылки.

10. По объему излагаемой информации документ является достаточно полным, отражает наряду с общетехническими требованиями, требования безопасности, устанавливаемые к объекту, их классификацию, правила приемки, методы испытаний, а также правила маркировки и упаковки.

11. В НПБ 305-2001 приводятся ссылки на пакет нормативных документов, используемых для разработки документов, так и необходимых для пользователей этим документом, что значительно облегчает работу пользователей и позволяет сокращать затраты времени на поиск необходимой информации.

Термины и определения

Единица физической величины – это физическая величина фиксированного размера, которой условно присвоено числовое значение, равное единице.

Измерение – нахождение значения физической величины опытным путем с помощью специальных технических средств.

Результат измерений – значение характеристики, полученное выполнением регламентированного метода измерений. В простейшем случае результат измерений (испытаний) является собственно наблюдаемым значением.

Единство измерений – состояние измерений, при котором их результаты выражены в указанных единицах, а погрешности известны с заданной вероятностью и не выходят за установленные пределы.

Достоверность – степень соответствия среднего значения, полученного в ходе проведения большого числа наблюдений, опорному значению. Достоверность измерений – это близость к нулю случайной или (неисключенной) систематической погрешности.

Повторяемость (сходимость) – степень совпадения наблюдаемых значений или результатов независимых испытаний, полученных при заданных условиях на идентичных установках в одной лаборатории.

Воспроизводимость – степень совпадения наблюдаемых значений или результатов независимых испытаний полученных при заданных условиях на идентичных установках в различных лабораториях.

Точность – это близость результатов измерений к принятому опорному значению.

Правильность – степень близости среднего значения, полученного на основании большой серии результатов измерений (испытаний), к принятому опорному значению.

Прецизионность – степень близости друг к другу независимых результатов измерений, полученных в конкретных регламентированных условиях. Прецизионность зависит только от случайной составляющей погрешности и не имеет отношения к опорному значению измеряемой величины.

Воспроизводимость результатов – характеристика результатов испытаний, определяемая близостью результатов повторных испытаний объекта.

Выброс (промах) – наблюдения в выборке, настолько отличающееся по своим значениям от остальных, что напрашивается предположение об их принадлежности к другой совокупности или неправильном выборе метода статистического анализа. Согласно ГОСТ Р ИСО 5725-1-2002, выбросом называется элемент совокупности значений, который не совместим с остальными элементами данной совокупности.

Погрешностью называют отклонение результата измерений от опорного значения измеряемой величины. При этом следует иметь в виду, что опорное значение физической величины считается неизвестным и применяется в теоретических исследованиях, а действительное значение³ устанавливается экспериментальным путём в предположении, что результат эксперимента (измерения) в максимальной степени приближается к опорному значению. Погрешности измерений приводятся обычно в технической документации на средства измерений или в нормативных документах.

Погрешность измерений – это отклонение результата измерений от опорного значения измеряемой величины. При измерениях получить опорное значение измеряемой величины невозможно, т.к. в результате любого познавательного процесса невозможно получить абсолютную истину. Поэтому результату любого измерения всегда присуща погрешность.

Случайная составляющая погрешности – это составляющая погрешности, изменяющаяся случайным образом при измерениях одной и той же величины. Случайная составляющая вызывает вариацию (разброс) результатов.

Систематическая составляющая погрешность (смещение) – это разность между математическим ожиданием результатов измерений и опорным значением. Если математическое ожидание систематической погрешности известно и постоянно, то в результате измерений вносят соответствующую поправку. Знак поправки противоположен знаку погрешности. Систематическая составляющая погрешности устойчиво искажает (смещает) результаты измерений.

Грубая погрешность – погрешность, которая явно и резко искажает результаты измерений. Они обычно исключаются из результата наблюдения (это неправильный отсчёт по шкале, неправильная запись в журнале). Грубые погрешности, как правило, возникают при однократных измерениях и обычно устраняются путём повторных измерений.

Многократные измерения – измерения одного и того же размера физической величины следующие друг за другом, проводящиеся с целью уменьшения случайной составляющей погрешности.

Генеральная совокупность –группа множеств (совокупностей), часто отражающая различные характеристики рассматриваемых изделий (объектов или материалов).

Доверительный интервал – интервал, которой с заданной вероятностью накроет неизвестное значение оцениваемого параметра распределения.

Доверительная вероятность – вероятность того, что доверительный интервал накроет действительное значение параметра оцениваемого по выборочным данным.\