
- •Глава 1. Линейная и векторная алгебра
- •Глава 2. Системы координат
- •Глава 3. Прямая на плоскости
- •Глава 4. Плоскость в пространстве
- •Глава 5. Прямая в пространстве
- •Глава 6. Кривые второго порядка
- •Глава 7. Поверхности второго порядка
- •Глава 8. Дифференциальная геометрия
- •Глава 9. Предел функции в точке
- •Глава 10. Дифференциальное исчисление функции одной переменной
- •Глава 11. Функции нескольких переменных
- •Глава 12. Неопределенный интеграл
- •§1 Основные методы интегрирования
- •Глава 13. Определенный интеграл
Глава 1. Линейная и векторная алгебра
§1 Матрицы |
||
1. Матрица, элементы матрицы |
Прямоугольная
таблица, составленная из
|
А= 1,
2,
3 – элементы первой строки. 3,5 – элементы
третьего столбца. Элемент
|
2. Симметрическая матрица |
Если amn = anm , то матрица называется симметрической |
|
3. Квадратная матрица. Главная и побочная диагонали квадратной матрицы. |
Матрица, у которой число строк равно числу ее столбцов называется квадратной матрицей. При этом число ее строк (столбцов) называется порядком матрицы.
В
квадратной матрице числа
|
Матрица
|
4. Диагональная матрица |
Квадратная матрица, у которой все числа, не стоящие на главной диагонали, равны нулю, называется диагональной матрицей. |
Квадратная
матрица вида
|
5. Единичная матрица |
Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной матрицей. Единичную матрицу обозначают прописной буквой Е |
Матрица
|
6. Матрица-строка, матрица-столбец. |
Матрица, состоящая только из одной строки, называется матрицей-строкой, состоящая только из одного столбца матрицей - столбцом. |
Матрица А=(2 0 5 4) есть матрица – строка. В
=
|
7. Транспониро- ванная матрица |
Матрица
|
|
8. Равенство матриц |
Две матрицы А и В называются равными (A=B), если они имеют одинаковые размеры и равные соответствующие элементы. |
Если
|
9. Сумма матриц |
Пусть
даны матрицы
Суммой
матриц А и
В называется матрица
Сумма
матриц подчиняется переместительному
и
сочетательному
законам,
т.е.
|
Задача. Если
Задача. Даны
матрицы
Решение.
|
10. Умножение матрицы на число |
Произведением
матрицы
размеров
Умножение
матрицы на число подчиняется закону
|
Задача. Если
|
11. Умножение матриц |
Произведением
матрицы А
размеров
на матрицу В размеров
|
Задача. Даны
Так
как число столбцов матрицы А равно
числу строк матрицы В, то произведение
Задача.
Даны
Решение. Матрица А имеет два столбца, В - две строки; следовательно, определено.
|
|
§2 Определители |
|||
12. Понятие определителя. Определитель второго порядка. |
Определитель – это число, которое по специальным правилам вычисляется для каждой квадратной матрицы. Определителем
второго порядка,
соответствующим заданной матрице А,
называется число равное
Для
обозначения определителя используются
вертикальные черточки и прописная
буква
|
|
|
13. Определитель третьего порядка |
Определителем третьего порядка, соответствующим данной квадратной матрице А, называется число
Элементы
|
Задача. Вычислить
определитель матрицы
Решение.
|
14. Минор |
Минором
|
Задача. Дано:
Решение.
Ответ. – 2. |
15. Алгебраичес-кое дополнение |
Алгебраическим
дополнением
элемента
,
где
,
называется
минор
|
Задача. Дано:
.
Найти
Решение.
Ответ. 2. |
||||||
16.
Определи-тели
порядка |
Определитель
и определяется как число
|
Задача. Вычислить
определитель
Значение
определителя:
|
||||||
17. Понятие вырожденной и невырожденной матрицы |
Обозначим
через
определитель матрицы
и вычислим его. Тогда, если
|
Так
как
|
||||||
18. Обратная матрица |
Квадратная
матрица
где
Всякая
неособенная матрица
имеет обратную матрицу
где
|
Задача. Дана
матрица
Решение. det A = 4 - 6 = -2.
M11=4; M12= 3; M21= 2; M22=1 x11= -2; x12= 1; x21= 3/2; x22= -1/2
Таким
образом,
|
||||||
19. Ранг матрицы |
Наибольший
из порядков миноров данной матрицы,
отличных от нуля, называется рангом
матрицы.
Обозначается
|
Задача. Дана
матрица
Имеем
Минор четвертого порядка составить нельзя. Ответ.
|
||||||
20. Определение ранга матрицы методом элементарных преобразований |
Простейший способ определения ранга матрицы состоит в приведении ее к ступенчатому виду при помощи последовательности элементарных преобразований. К ним относятся: - умножение строки на произвольное число, отличное от нуля; - прибавление к некоторой строке любой другой строки, умноженной на одно и тоже число; - вычеркивание нулевой строки.
|
Задача. Найти
ранг матрицы
Решение. После
вычитания первой строки из остальных
получаем эквивалентную матрицу, а из
последней умноженную на 2,
Поскольку
три строки промежуточной матрицы были
пропорциональны, то из них можно
получить две ненулевые строки, которые
мы отбросили. Ясно, что
|
||||||
21. Совместная и несовместная система линейных уравнений. Определенная и неопределенная система линейных уравнений. Теорема Кронекера – Капелли.
|
Система, имеющая хотя бы одно решение, называется совместной, имеющая только одно решение определенной, имеющая более одного решения - неопределенной, не имеющая ни одного решения - несовместной.
Теорема 1. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы
|
Задача. Определить совместность системы линейных уравнений:
|
||||||
|
Теорема 2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение. Теорема 3. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений. |
Ранг A = 2
Ранг
|
||||||
22. Решение системы линейных уравнений по формулам Крамера |
Теорема. Система из n уравнений с n неизвестными
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам: xi = i /, где = det A, а i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
|
Задача. Решить по формулам Крамера систему уравнений
Решение. Система содержит одинаковое число уравнений и неизвестных. Вычислим определитель этой системы.
Так как ,то решение можно найти по формулам Крамера:
Тогда
Ответ. {1;2}.
|
||||||
23. Решение систем линейных уравнений матричным методом |
Задача. Решить матричным способом систему уравнений
Решение. Система
содержит одинаковое число уравнений
и неизвестных. Вычислим определитель
этой системы:
Тогда
|
|||||||
24. Решение систем линейных уравнений методом Гаусса. |
Метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных. Рассмотрим систему линейных уравнений:
Разделим обе части 1–го уравнения на a11 0, затем: 1) умножим на а21 и вычтем из второго уравнения; 2) умножим на а31 и вычтем из третье и т.д. Получим:
где
j = 2, 3, … , n+1. Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.
|
Задача. Решить систему методом Гаусса.
Решение. Составим расширенную матрицу системы.
Таким образом, исходная система может быть представлена в виде:
откуда получаем: z = 3; y = 2; x = 1.
|
||||||
§3 Векторы |
||||||||
25. Вектор. Координаты вектора. |
Вектором
называется направленный отрезок.
Пусть точка
есть начало вектора, а точка
Если
заданы 2 точки в пространстве
|
З Дано:
Решение.
Ответ.
|
||||||
26. Модуль вектора |
Расстояние
между началом и концом вектора
называется длиной
вектора или
его
модулем.
Модуль вектора обозначается символами
Длина
вектора в координатах
определяется как расстояние между
точками начала и конца вектора. Если
заданы две точки в пространстве
,
,
то
Если
|
Задача. Дано:
,
.
Найти
Решение.
Ответ.
|
||||||
27. Нулевой вектор |
Вектор,
начало которого совпадает с его концом,
называется нулевым
и обозначается
|
|
||||||
28. Понятие коллинеарных векторов |
Векторы, расположенные на одной прямой или параллельных прямых, называются коллинеарными.
Пусть
векторы
|
Задача. При
каких
Решение. Так
как
Отсюда
находим, что
|
||||||
29. Понятие компланарных векторов |
Векторы, расположенные на одной плоскости или на параллельных плоскостях, называются компланарными. |
векторы
|
||||||
30. Понятие равенства векторов |
Два
вектора
|
|
||||||
31. Противопо- ложный вектор |
Вектор
|
|
||||||
32. Единичный вектор |
Вектор,
длина которого равна единице, называется
единичным
вектором,
обозначается символом
|
Задача. (Координаты единичного вектора). Определить
координаты единичного вектора
,
если
Решение.
следовательно,
|
||||||
33. Направляющие косинусы вектора |
Обозначим
через
|
Задача. Вектор
Решение. Находим
проекции вектора
на координатные оси:
Ответ. ; ; . |
||||||
34. Сумма векторов |
Суммой
векторов
и
Пусть векторы и заданы в координатной форме:
Сумма
векторов:
|
Задача. Дано:
Решение.
Ответ.
|
||||||
35. Разность векторов |
Разностью
векторов
Разность векторов в координатной форме:
|
Задача. Дано:
,
.
Найти
Решение.
Ответ.
|
||||||
36. Умножение векторов |
Пусть
даны вектор
и число
.
Произведением
вектора
на число
называется вектор
Произведение
вектора
= |
Задача. Дано:
Решение. 3 ={6;0;9}. Ответ. {6;0;9}.
|
||||||
37. Деление отрезка в данном отношении |
Если
точка
В
частности, при
|
Задача. Даны
точки
Решение.
Следовательно,
искомая точка
Ответ. . |
||||||
38. Проекция вектора на ось |
П
|
Задача. Вычислить
проекцию вектора
Решение.
Следовательно,
Ответ.
|
||||||
39. Скалярное произведение векторов |
Скалярным
произведением векторов
Свойства скалярного произведения: 1)
2)
3)
5)
Если
рассматривать векторы
|
Задача. Найти
скалярное произведение
Решение.
Ответ. 336.
|
||||||
40. Определение угла между векторами. Геометрический смысл скалярного произведения векторов. |
Так
как
|
Задача. Даны
вершины треугольника
Решение. Построим
векторы
Ответ.
|
||||||
41.Ортогональность векторов |
Если
Условие называется условием перпендикулярности двух векторов
|
Задача. При
каком m
векторы
Решение.
Ответ.
|
||||||
42. Физический смысл скалярного произведения векторов |
Задача. Вычислить
работу по перемещению материальной
точки вдоль отрезка,
из точки
Решение. Из
курса физики
известно,
что работа
,
совершаемая
при указанных
в примере условиях, находится по
формуле
Ответ. 5.
|
|||||||
43. Векторное произведение векторов |
Векторным
произведением векторов
и
называется вектор
Свойства векторного произведения векторов: 1 2)
3)
4)
Введем
декартовую систему координат
и рассмотрим
векторные произведения единичных
векторов
|
|||||||
44. Векторное произведение векторов в координатной форме |
Если
заданы векторы
|
Пример.
Найти векторное произведение векторов
|
||||||
45. Нахождение площади параллелограмма. Геометрическое приложение векторного произведения векторов. |
П
|
Задача. Даны
вершины треугольника
Решение. Найдем
векторы
Так
как
Ответ. 14. Задача. Найти
площадь параллелограмма, построенного
на векторах
Ответ. 4. |
||||||
46. Механическое приложение векторного произведения векторов |
Задача. Сила
Решение. Пусть
точка
есть
некоторая точка
Ответ.
|
|||||||
47. Смешанное произведение векторов |
Смешанным произведением векторов , и называется число, равное скалярному произведению вектора на вектор, равный векторному произведению векторов и . Обозначается
Смешанное
произведение
Свойства смешанного произведения: 1) Смешанное произведение равно нулю, если: а) хоть один из векторов равен нулю; б) два из векторов коллинеарны; в) векторы компланарны; 2)
3)
4)
5)
Объем треугольной пирамиды, образованной
векторами
,
и
,
равен
|
|||||||
48. Смешанное произведение векторов в координатной форме |
Если
то
|
Задача. Даны
векторы
Вычислить
Решение.
Ответ.
|
49. Геометрическое приложение смешанного произведения векторов. Вычисление объема параллелепипеда. |
М
|
Задача. Вычислить
Решение.
|
50. Необходимое и достаточное условия компланарности трех векторов, заданных в координатной форме |
Для
того, чтобы три вектора
|
Задача. При
каком значении
Решение.
Векторы
компланарны, если
Ответ. 1. |
51. Норма вектора в евклидовом пространстве. Нормирование вектора.
|
Линейное
пространство, в котором определена
операция скалярного умножения,
называется евклидовым
и обычно обозначается E.
Нормой
(длиной) вектора
|
Задача. Укажите
соответствие между заданным вектором
и соответствующим ему нормированным
вектором
1.
3.
Ответ.
Задача. В
евклидовом пространстве
|
|
Вектор, норма которого равна единице, называется единичным (нормированным) вектором, или ортом. |
Решение. Длина нормированного вектора равна единице, следовательно
Ответ. . |
52. Характеристи-ческий многочлен матрицы. Собственный вектор матрицы.
|
Характеристическим уравнением матрицы
называется уравнение
Корни
этого уравнения
Система уравнений
в
которой
имеет одно из значений
и определитель которой в илу этого
равен нулю, определяет тройку чисел
Эта
совокупность трех чисел
с точностью до постоянного множителя
определяет ненулевой вектор
|
Задача. Дана
матрица
Решение.
Подставив
значение
,
приходим к соотношению
|


 -
симметрическая матрица
-
симметрическая матрица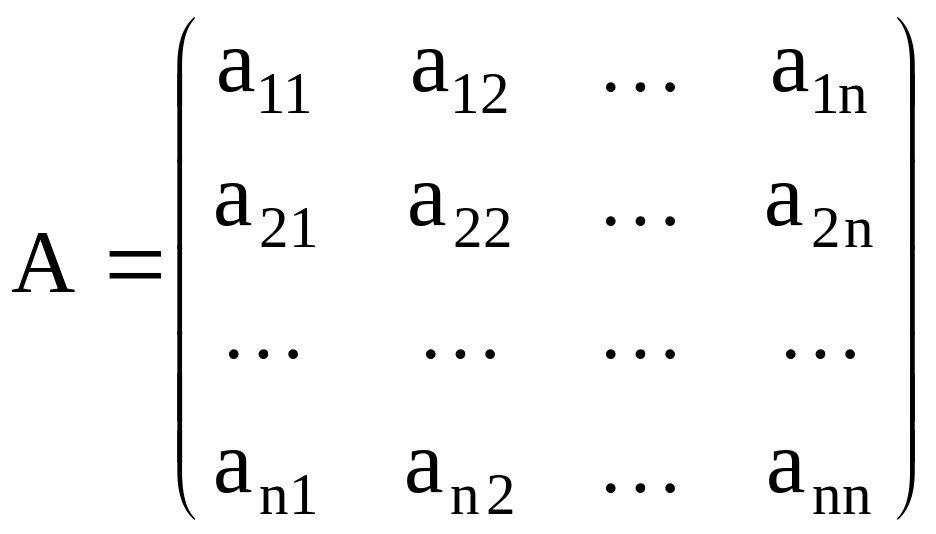
 есть квадратная матрица третьего
порядка. 1,0,7 – элементы главной
диагонали.
есть квадратная матрица третьего
порядка. 1,0,7 – элементы главной
диагонали. называется диагональной
матрицей.
называется диагональной
матрицей.
 единичная матрица третьего порядка
единичная матрица третьего порядка
 ;
;
 ,
найти 2А + В.
,
найти 2А + В. ,
,
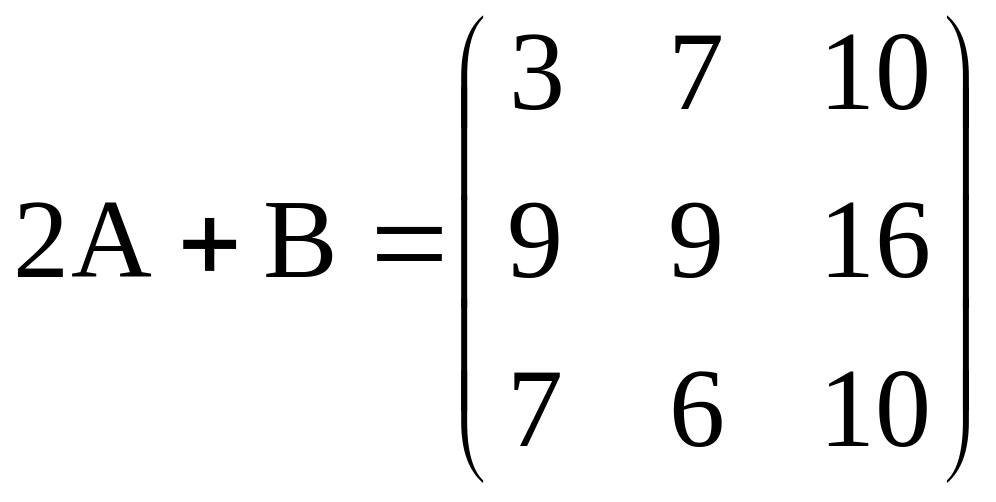 .
. для всех
для всех
 ,
,
 .
.


 .
Найти
.
Найти

 где
где
 .
.

 .
.
 .
.
 ,
,
 .
Определить ее ранг. Решение.
.
Определить ее ранг. Решение.
 .
.
 .
.
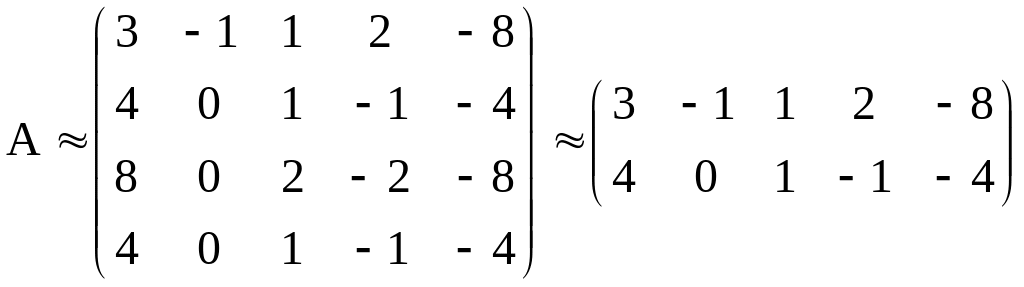 .
.

 ;
;
 ;
;
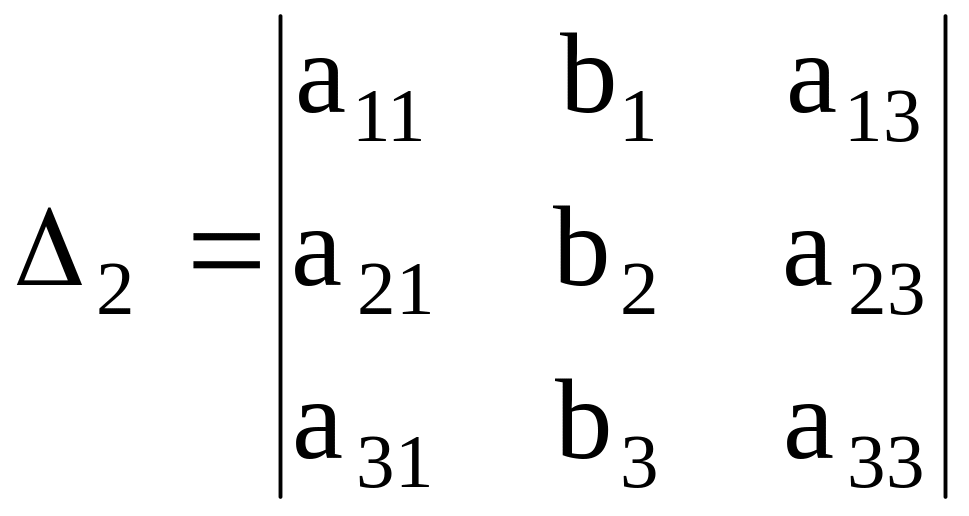 ;
;
 ;
;



 .
Так как
,
то система имеет единственное решение.
Составим матрицы
.
Так как
,
то система имеет единственное решение.
Составим матрицы
 Так как определитель системы
Так как определитель системы
 Вычислим алгебраические дополнения
Вычислим алгебраические дополнения

 .
.
 адача.
адача.

 .
.

 .
.
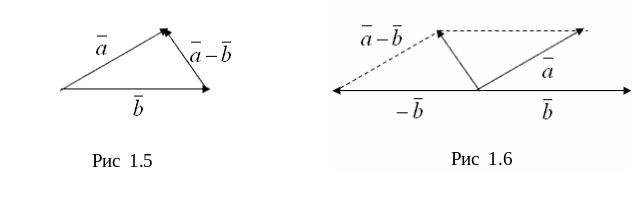
 роекция
вектора
на ось
роекция
вектора
на ось
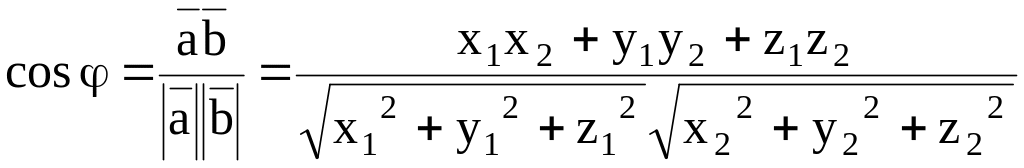
 )
)


 лощадь
параллелограмма, построенного на
векторах
лощадь
параллелограмма, построенного на
векторах
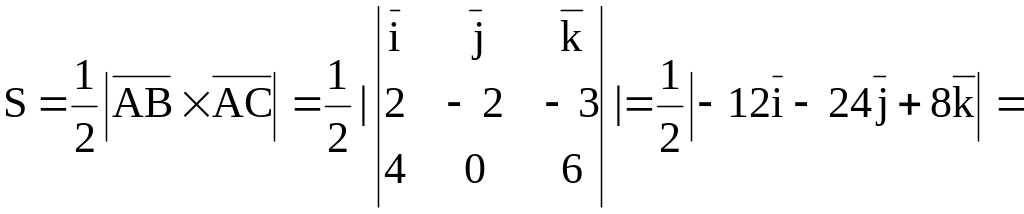
 .
.
 .
. одуль
смешанного произведения численно
равен объему
одуль
смешанного произведения численно
равен объему
 .
Ответ.
.
Ответ.

 .
.
 .
.